Asistencia gravitatoria para niños
En astronáutica, la asistencia gravitatoria es una técnica especial que usan las naves espaciales. Consiste en aprovechar la fuerza de gravedad de un planeta o luna para que la nave gane velocidad, la pierda o cambie de dirección. Es como si el planeta le diera un "empujón" o la "frenara" sin que la nave gaste su propio combustible.
En inglés, a esta técnica se le llama slingshot effect (efecto honda), swing-by (hamacarse) o gravity assist (asistencia de gravedad). Es muy común en las misiones que viajan a los planetas más lejanos de nuestro sistema solar.
Para ahorrar combustible en el cohete de lanzamiento, los científicos diseñan rutas complejas. Estas rutas hacen que la nave pase cerca de uno o varios planetas antes de llegar a su destino final. Para que esto funcione, los planetas deben estar en la posición correcta en el espacio. Por eso, las misiones espaciales tienen momentos muy específicos para ser lanzadas, llamados "ventanas de lanzamiento".
Plantilla:Ficha de concepto
Asistencia Gravitatoria: El Impulso de los Planetas
La asistencia gravitatoria es una forma inteligente de usar la gravedad de los cuerpos celestes. Permite que las naves espaciales viajen más lejos y más rápido, o que lleguen a su destino con menos combustible.
¿Cómo Funciona la Asistencia Gravitatoria?
Imagina que una nave espacial se acerca a un planeta. La gravedad del planeta la atrae y la acelera. Al pasar cerca, la nave "roba" un poco de la energía de movimiento del planeta. Esto hace que la nave cambie su velocidad y dirección. El planeta, al ser tan grande, apenas nota este cambio.
Cuando una nave espacial se acerca a un planeta que se mueve, la gravedad del planeta la atrae. La nave se acelera mientras se acerca al planeta. Al pasar por detrás del planeta, la nave es "lanzada" hacia adelante, ganando velocidad. Es como si el planeta le diera un empujón.
Por ejemplo, si un planeta se mueve a una velocidad U y la nave se acerca a una velocidad v, la nave puede salir con una velocidad cercana a v + 2U. Esto significa que su velocidad aumenta significativamente. Este aumento de velocidad se logra sin gastar el combustible de la nave.
La asistencia gravitatoria también se puede usar para frenar una nave. En este caso, la nave se acerca al planeta por delante, en la dirección de su movimiento. Al pasar, la nave transfiere parte de su energía al planeta, lo que la frena.
La sonda Mariner 10 usó esta técnica en 1974 para llegar a Mercurio. La misión MESSENGER también la utilizó para alcanzar el mismo planeta.
¿Por Qué es Importante la Asistencia Gravitatoria?
Los cohetes necesitan mucho combustible para salir de la Tierra y viajar por el espacio. Cuanto más lejos va una misión, más combustible necesita. El combustible es muy pesado, y llevar más combustible significa que el cohete debe ser más grande y potente.
La asistencia gravitatoria permite a las naves cambiar su velocidad y dirección sin usar sus propios motores. Esto ahorra una gran cantidad de combustible. Al ahorrar combustible, las misiones pueden ser más baratas, llevar más instrumentos científicos o viajar a destinos más lejanos. Es una técnica clave para la exploración del espacio profundo.
Pioneros de la Asistencia Gravitatoria
La idea de usar la gravedad de los planetas no es nueva.
- El primero en proponer usar la gravedad de un planeta para dirigir una sonda fue Giuseppe Colombo (1920-1984). Él fue un matemático e ingeniero italiano.
- En 1938, Yuri Kondratyuk sugirió que una nave espacial podría ser acelerada usando la gravedad de las lunas de los planetas.
- Friedrich Zander, en 1925, también entendió cómo la asistencia gravitatoria podía ayudar a la exploración interplanetaria.
- El ingeniero italiano Gaetano Arturo Crocco fue el primero en calcular un viaje interplanetario usando múltiples asistencias gravitatorias.
La primera vez que se intentó esta maniobra fue en 1959. La sonda soviética Luna 3 la usó para fotografiar la cara oculta de la Luna.
En 1961, Michael Minovitch, un estudiante que trabajaba en el Laboratorio de Propulsión a Reacción (JPL) de la NASA, desarrolló la técnica de asistencia gravitatoria. Más tarde, esta técnica fue clave para la idea del "Gran Viaje Planetario" de Gary Flandro.
Gary Flandro descubrió una alineación poco común de los planetas exteriores (Júpiter, Saturno, Urano y Neptuno). Esto le permitió concebir una misión que visitaría varios planetas, reduciendo el tiempo de viaje de cuarenta años a menos de diez.
Misiones Famosas que Usaron Asistencia Gravitatoria
Muchas misiones espaciales han usado la asistencia gravitatoria para llegar a sus destinos:
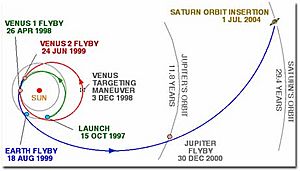
- La misión espacial Cassini/Huygens usó la gravedad de Venus dos veces, la Tierra y Júpiter. Gracias a esto, llegó a Saturno en 7 años.
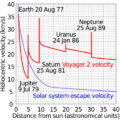
- La sonda Voyager 2 usó la asistencia gravitatoria de Júpiter, Saturno y Urano para acelerar y visitar estos planetas. Luego, pasó por Neptuno para observar su luna Tritón.
- La Mariner 10 y la MESSENGER usaron la asistencia gravitatoria para frenar y llegar a Mercurio.
El aumento máximo de velocidad que un planeta puede dar depende de su tamaño y de cuán cerca pase la nave. Por ejemplo:
- Venus puede dar hasta 7 km/s.
- La Tierra puede dar hasta 8 km/s.
- Marte puede dar hasta 3.5 km/s.
- Júpiter puede dar hasta 43 km/s.
- Saturno puede dar hasta 26 km/s.
Galería de imágenes
Véase también
 En inglés: Gravity assist Facts for Kids
En inglés: Gravity assist Facts for Kids
- Órbita de transferencia de Hohmann: una técnica para cambiar la órbita de una nave.
- Guido von Pirquet (1880-1966): pionero austriaco de la asistencia gravitatoria.
- Gaetano Arturo Crocco (1877-1968): científico militar italiano que ideó un "Gran Tour" para visitar Venus y Marte.
- Giuseppe Colombo (1920-1984): científico italiano que trabajó en misiones a Mercurio.