Transformada de Laplace para niños
La transformada de Laplace es una herramienta matemática muy útil que ayuda a resolver problemas difíciles. Imagina que tienes un problema complicado en un idioma (por ejemplo, el tiempo) y lo traduces a otro idioma (una variable compleja) donde es mucho más fácil de resolver. Una vez que lo resuelves en el nuevo idioma, puedes "traducir" la solución de vuelta al idioma original.
Esta herramienta es especialmente buena para resolver ecuaciones diferenciales, que son ecuaciones que describen cómo cambian las cosas con el tiempo, como el movimiento de un objeto o el flujo de electricidad. La transformada de Laplace convierte estas ecuaciones complejas en ecuaciones algebraicas más sencillas, que son como las que resuelves en la escuela.
Plantilla:Ficha de concepto matemático
Contenido
Historia de la Transformada de Laplace
La transformada de Laplace lleva el nombre de un famoso matemático francés llamado Pierre-Simon Laplace. Él la presentó por primera vez en 1782, mientras trabajaba en la teoría de la probabilidad.
Antes de Laplace, otros matemáticos como Leonhard Euler y Joseph Louis Lagrange ya habían investigado tipos de integrales (que son como sumas infinitas) parecidas. Ellos buscaban formas de usar estas integrales para resolver ecuaciones difíciles.
Laplace dio un paso importante: en lugar de solo usar estas integrales como soluciones, pensó en aplicarlas a las ecuaciones para transformarlas. Así, una ecuación diferencial (que describe cambios) se convertía en una ecuación algebraica (que es más sencilla de manejar). Él descubrió algunas de las propiedades principales de esta transformación.
Sin embargo, después de Laplace, esta herramienta no fue muy usada por un tiempo. Se veía más como una idea matemática interesante que como algo práctico.
El regreso de la Transformada
La verdadera importancia de la transformada de Laplace se descubrió mucho después, a finales del siglo XIX. Un ingeniero inglés llamado Oliver Heaviside (1850-1925) estaba tratando de resolver ecuaciones relacionadas con las vibraciones y los circuitos eléctricos. Él encontró una manera de tratar las partes de las ecuaciones que indicaban cambios (operadores diferenciales) como si fueran números normales.
Heaviside desarrolló un método que era muy útil para los ingenieros y físicos, aunque no era muy "riguroso" (es decir, no estaba completamente justificado con las reglas matemáticas de la época). Muchos matemáticos al principio no lo aceptaron.
Pero como el método de Heaviside funcionaba tan bien, los ingenieros lo adoptaron rápidamente. Esto hizo que los matemáticos volvieran a interesarse y buscaran una base sólida para él. Fue entonces cuando se dieron cuenta de que la transformada que Laplace había descubierto un siglo antes no solo justificaba el método de Heaviside, sino que también ofrecía una forma mucho más organizada de resolver esos problemas.
A principios del siglo XX, la transformada de Laplace se volvió una herramienta fundamental en campos como la teoría de vibraciones y la teoría de circuitos. Una de sus mayores ventajas es que convierte operaciones complicadas como la integración y la derivación en operaciones más simples como la multiplicación y la división. Esto hace que las ecuaciones difíciles se conviertan en ecuaciones de polinomios, que son mucho más fáciles de resolver.
¿Cómo se define la Transformada de Laplace?
La transformada de Laplace toma una función que depende del tiempo, digamos 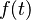 , y la convierte en una nueva función que depende de una variable compleja
, y la convierte en una nueva función que depende de una variable compleja  , a la que llamamos
, a la que llamamos 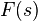 .
.
La forma de hacer esta "transformación" es a través de una integral especial:
No te preocupes si la fórmula parece complicada. Lo importante es entender que es una "receta" para cambiar la función 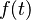 a
a 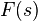 .
.
Notación
Para no escribir toda la integral cada vez, usamos un símbolo especial para la transformada de Laplace: 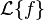 o
o 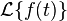 . La letra
. La letra 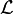 se llama el operador de la transformada de Laplace.
se llama el operador de la transformada de Laplace.
Propiedades importantes
La transformada de Laplace tiene varias propiedades que la hacen muy útil. Aquí te explicamos algunas de las más importantes de forma sencilla:
Linealidad
Esta propiedad significa que si tienes una suma de funciones o una función multiplicada por un número, puedes aplicar la transformada a cada parte por separado. Es como decir que la transformada es "justa" y se distribuye.
Primer teorema de traslación
Si multiplicas tu función original por Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): e^{at} (una función exponencial), la transformada de Laplace de esa nueva función es la misma que la original, pero con la variable  "desplazada" por
"desplazada" por 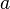 .
.
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathcal{L}\left\{ e^{at} f(t) \right\} = F(s-a)
Segundo teorema de traslación
Si tu función original se "activa" después de un cierto tiempo 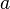 (esto se representa con la función escalón unitario), su transformada de Laplace se multiplica por Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): e^{-as} . Esto es útil para funciones que empiezan en un momento específico.
(esto se representa con la función escalón unitario), su transformada de Laplace se multiplica por Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): e^{-as} . Esto es útil para funciones que empiezan en un momento específico.
Transformada de una derivada
¡Esta es una de las propiedades más poderosas! Convierte la operación de derivación (que mide cómo cambia algo) en una simple multiplicación por  . Esto es lo que hace que las ecuaciones diferenciales sean mucho más fáciles de resolver.
. Esto es lo que hace que las ecuaciones diferenciales sean mucho más fáciles de resolver.
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathcal{L}\{f^{(n)}(t)\}(s)=s^n\mathcal{L}\{f(t)\}(s)-s^{n-1}f(0)-s^{n-2}f'(0)-\cdots-f^{(n-1)}(0)
Transformada de una integral
De manera similar a la derivada, la transformada de una integración (que es como sumar continuamente) se convierte en una división por  .
.
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathcal{L}\left\{\int_0^tf(u)\;du\right\}(s)=\frac{\mathcal{L}\{f(t)\}(s)}{s}
Convolución
La convolución es una operación especial entre dos funciones. La transformada de Laplace convierte esta operación compleja en una simple multiplicación de las transformadas de cada función.
Ejemplos sencillos
Para entender mejor, veamos algunos ejemplos de cómo funciona la transformada de Laplace:
Ejemplo 1: La transformada de un número constante
Si tenemos una función muy simple, como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(t)=1 (es decir, una línea recta horizontal), su transformada de Laplace es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{1}{s} .
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathcal{L}\{1\} = \frac{1}{s}
Ejemplo 2: La transformada de una función exponencial
Si tenemos la función 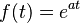 (una función que crece o decrece muy rápido), su transformada de Laplace es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{1}{s-a} .
(una función que crece o decrece muy rápido), su transformada de Laplace es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{1}{s-a} .
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathcal{L}\{e^{at}\} = \frac{1}{s-a}
Ejemplo 3: La transformada de la función seno
Para una función como 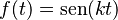 (que describe ondas), su transformada de Laplace es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{k}{s^2+k^2} .
(que describe ondas), su transformada de Laplace es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{k}{s^2+k^2} .
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathcal{L}\{\sen(kt)\} = \frac{k}{s^2+k^2}
Tabla de las transformadas de Laplace más comunes
Aquí tienes una tabla con algunas de las transformadas de Laplace más usadas. Como la transformada de Laplace es "lineal", puedes sumar las transformadas de funciones separadas.
| ID | Función | Dominio en el tiempo |
Dominio en la frecuencia Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): X(s) |
|---|---|---|---|
| 1 | Impulso unitario | 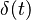 |
 |
| 2 | Amortiguación exponencial | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): e^{-\alpha t} \ | 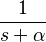 |
| 3 | Potencia con desplazamiento |
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \ t^n \cdot e^{-\alpha t} | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{n!}{(s+\alpha)^{n+1}} |
| 4 | Escalón unitario | 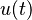 |
 |
| 5 | Escalón unitario con retraso | 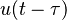 |
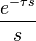 |
| 6 | n-ésima potencia | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): { t^n } | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): { n! \over s^{n+1} } |
| 7 | Seno | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sen(\omega t) \ | 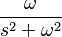 |
| 8 | coseno | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \cos(\omega t) \ | 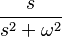 |
| 9 | seno hiperbólico | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sinh(\alpha t) \ | 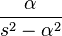 |
| 10 | coseno hiperbólico | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \cosh(\alpha t) \ | 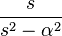 |
| Notas explicativas: | |||
Relación con otras transformadas
La transformada de Laplace está muy relacionada con otras herramientas matemáticas como la transformada de Fourier y la transformada Z. Todas ellas son formas de cambiar una función de un "dominio" a otro para hacer los problemas más fáciles de resolver.
Galería de imágenes
Véase también
 En inglés: Laplace transform Facts for Kids
En inglés: Laplace transform Facts for Kids
- Causalidad (física)
- Transformada de Mellin
Bibliografía
- Spiegel, Murray R. (2014). Transformadas de Laplace. McGraw Hill Interamericana de México.
Enlaces externos
- Fernández Rodríguez, César René (2006). Transformada de Laplace y Ecuaciones de Volterra (PDF). Universidad de Santiago de Chile. Consultado el 20 de abril de 2020.
-
Esta obra contiene una traducción parcial derivada de «Laplace transsform» de Wikipedia en inglés, concretamente de esta versión, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported.


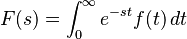
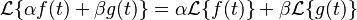
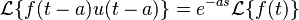
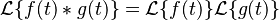
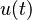 representa la
representa la 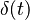 representa la
representa la 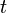 normalmente representa el tiempo.
normalmente representa el tiempo. es una variable compleja que representa la frecuencia.
es una variable compleja que representa la frecuencia.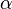 ,
, 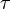 , y
, y 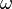 son números reales.
son números reales.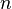 es un número entero.
es un número entero.