Función escalón de Heaviside para niños
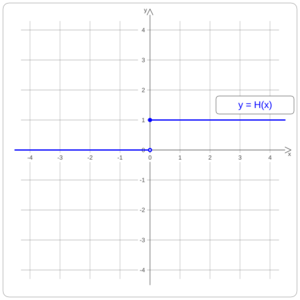
La función escalón de Heaviside, también conocida como función escalón unitario, es una herramienta matemática muy útil que lleva el nombre del matemático inglés Oliver Heaviside. Imagina que es como un interruptor de luz: está "apagada" (su valor es 0) para todos los números negativos, y se "enciende" (su valor es 1) para todos los números positivos, incluyendo el cero.
En términos sencillos, si tienes un número x:
- Si x es menor que 0 (por ejemplo, -5, -1), la función vale 0.
- Si x es igual o mayor que 0 (por ejemplo, 0, 2, 100), la función vale 1.
A veces, esta función se representa con la letra H(x).
Contenido
¿Para qué se usa la función escalón de Heaviside?
Esta función es muy importante en campos como la ingeniería de control y el procesamiento de señales. Piensa en ella como una forma de describir algo que se activa o se enciende en un momento específico y luego permanece activo.
Por ejemplo:
- En ingeniería de control, puede representar el momento en que un sistema se enciende, como cuando un robot empieza a moverse.
- En procesamiento de señales, puede simular una señal eléctrica que comienza en un instante dado y se mantiene constante.
¿Cómo se define el valor en cero?
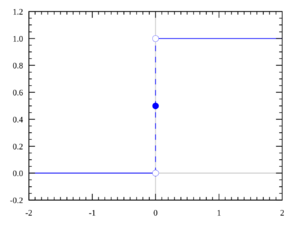
Aunque la idea principal de la función escalón es clara (0 antes de cero, 1 después de cero), a veces hay pequeñas diferencias en cómo se define exactamente el valor de la función cuando x es igual a 0.
La mayoría de las veces, se define que la función vale 1 cuando x es 0. Sin embargo, algunos matemáticos y científicos prefieren que valga 0, y otros incluso la definen como 1/2 en ese punto. Estas diferencias no cambian el comportamiento general de la función, solo su valor en un punto muy específico.
Galería de imágenes
-
La función escalón de Heaviside. Observa cómo "salta" de 0 a 1 en el punto cero.
-
función escalón considerando H(0)=1/2.
Véase también
- Continuidad (matemática)
- Función definida a trozos
- Función rectangular
- Función escalonada
- Función signo
- Valor absoluto
- Función rampa
