Delta de Dirac para niños
La delta de Dirac es una herramienta matemática muy especial, creada por el famoso físico británico Paul Dirac. Imagina que quieres describir algo que está concentrado en un solo punto, como una masa muy pequeña en un lugar exacto o un golpe muy rápido y fuerte. Para eso, la delta de Dirac es perfecta.
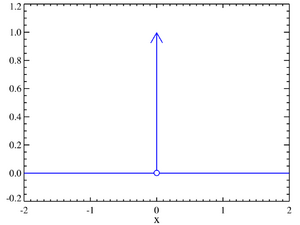
No es una función común, porque en un punto específico su valor es "infinito" y en todos los demás puntos es cero. Sin embargo, si sumas (o "integras") todos sus valores, el resultado es 1. Se usa mucho en física e ingeniería para modelar situaciones donde algo ocurre de forma muy puntual o instantánea. A veces, se le llama también función de impulso.
Contenido
¿Qué es la Delta de Dirac?
La delta de Dirac es una distribución o función generalizada. Esto significa que no se comporta como las funciones que normalmente estudias en matemáticas, que tienen un valor definido en cada punto. En cambio, la delta de Dirac se define por cómo interactúa con otras funciones.
¿Cómo se define la Delta de Dirac?
La forma más sencilla de entender la delta de Dirac es a través de una operación matemática llamada integral. Si tienes una función cualquiera, digamos f(x), y la "multiplicas" por la delta de Dirac y luego la integras, el resultado es el valor de esa función f(x) en el punto donde la delta de Dirac está "activa".
Por ejemplo, si la delta de Dirac está centrada en el punto 'a', se escribe como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \delta(x-a) . Cuando la integras con otra función f(x), obtienes: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \int_{-\infty}^\infty \delta(x-a) f(x) \, dx = f(a)
Esto significa que la delta de Dirac "selecciona" el valor de la función f(x) justo en el punto 'a'. Si f(x) fuera simplemente el número 1, entonces la integral de la delta de Dirac por sí misma sería 1: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \int_{-\infty}^\infty \delta(x-a) \, dx = 1
Esto es clave: aunque es "infinita" en un punto y cero en los demás, su "área" total es siempre 1.
¿Por qué no es una función normal?
Imagina una aguja muy, muy fina y alta. Tan fina que su ancho es casi cero, pero tan alta que llega al infinito. Esa es la idea de la delta de Dirac. Como no podemos dibujar una función que sea infinita en un punto y cero en todos los demás, y que además su área sea 1, decimos que es una "función generalizada" o una "distribución".
En física, la delta de Dirac puede representar la densidad de una masa muy pequeña concentrada en un solo punto. Es una forma de simplificar problemas complejos, tratando objetos muy pequeños como si fueran puntos matemáticos.
¿Cómo se relaciona con otras funciones?
La delta de Dirac también nos ayuda a entender los cambios bruscos en las funciones. Por ejemplo, está relacionada con la Función escalón de Heaviside, que es una función que vale 0 antes de un punto y 1 después de ese punto, como un interruptor que se enciende de golpe. La delta de Dirac es como la "velocidad de cambio" de esa función escalón.
Propiedades importantes de la Delta de Dirac
La delta de Dirac tiene varias propiedades que la hacen muy útil en matemáticas y ciencias. Aquí te mostramos algunas de las más importantes:
- Simetría: La delta de Dirac es simétrica, lo que significa que Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \delta(x)=\delta(-x) . Es como si fuera un espejo.
- Interacción con funciones: Si multiplicas una función
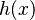por la delta de Dirac centrada en 'a', el resultado es el valor de 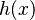en 'a' multiplicado por la delta de Dirac:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): h(x)\delta(x-a)=h(a)\delta(x-a) Esto refuerza la idea de que la delta de Dirac "extrae" el valor de la función en el punto donde está activa.
- Integral de dos deltas: Si integras dos deltas de Dirac, el resultado es otra delta de Dirac que indica la diferencia entre sus puntos de origen:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \int_{-\infty}^\infty \delta(x-a)\delta(x-b)\ dx=\delta(a-b)
Estas propiedades son muy valiosas para resolver ecuaciones y entender fenómenos en campos como la electrónica, la mecánica cuántica y el procesamiento de señales.
Galería de imágenes
-
Diagrama esquemático de la función delta de Dirac.
Véase también
En inglés: Dirac delta function Facts for Kids
- Delta de Kronecker
- Teoría de distribuciones
- Transformada de Laplace
