Teoría informal de conjuntos para niños
La Teoría Informal de Conjuntos es una forma de entender y trabajar con conjuntos, que son colecciones de objetos. Es una de las primeras ideas que surgieron para darle una base sólida a las matemáticas.
Los conjuntos son muy importantes en matemáticas. De hecho, muchas cosas en matemáticas, como los números, las relaciones y las funciones, se pueden explicar usando conjuntos.
Contenido
¿Qué es la Teoría Informal de Conjuntos?
La teoría informal de conjuntos es "no formalizada". Esto significa que usa el lenguaje de todos los días para hablar de conjuntos. Palabras como "y", "o", "no", "si... entonces" no tienen definiciones matemáticas súper estrictas.
Esta teoría comenzó a finales del XIX, gracias a matemáticos como Georg Cantor y Gottlob Frege. Querían que los matemáticos pudieran trabajar con conjuntos muy grandes, incluso infinitos, de una manera lógica.
Al principio, esta teoría permitía crear un conjunto a partir de cualquier característica, sin límites. Pero esto causó problemas, como las "paradojas lógicas". Un ejemplo famoso es la paradoja de Russell. Para solucionar esto, se creó la teoría axiomática de conjuntos. Esta nueva teoría puso reglas claras sobre cómo se podían definir los conjuntos. Hoy en día, a la teoría axiomática de conjuntos simplemente se le llama "teoría de conjuntos".
¿Qué son las paradojas?
Si uno asume que cualquier característica puede usarse para formar un conjunto sin restricciones, aparecen problemas lógicos llamados paradojas. La paradoja de Russell es un buen ejemplo. Imagina un conjunto que contiene a "todos los conjuntos que no se contienen a sí mismos". Si este conjunto se contiene a sí mismo, entonces no debería contenerse (por su definición). Pero si no se contiene a sí mismo, entonces sí debería contenerse (por su definición). ¡Es una contradicción! Por eso, las teorías de conjuntos necesitan reglas para evitar estas situaciones.
¿Por qué se crearon las teorías axiomáticas?
Las teorías axiomáticas de conjuntos se desarrollaron para responder a estos problemas. Su objetivo era definir con mucha precisión qué operaciones y definiciones de conjuntos estaban permitidas y cuáles no. Esto ayudó a evitar las paradojas que surgían en la teoría informal.
Conjuntos, elementos e igualdad
En la teoría informal de conjuntos, un conjunto es una colección de objetos bien definida. Estos objetos se llaman elementos o miembros del conjunto. Pueden ser cualquier cosa: números, personas, o incluso otros conjuntos. Por ejemplo, el número 4 es un elemento del conjunto de todos los números enteros.
Pertenencia a un conjunto
Si un objeto x es parte de un conjunto A, decimos que x pertenece a A. Esto se escribe así: x ∈ A. Si x no pertenece a A, lo escribimos así: x ∉ A.
Igualdad de conjuntos
Dos conjuntos, A y B, son iguales si tienen exactamente los mismos elementos. Esto significa que cada elemento de A también está en B, y cada elemento de B también está en A. Por ejemplo, el conjunto {2, 3, 5} es igual al conjunto de todos los números primos menores de 6. Si A y B son iguales, se escribe A = B.
El conjunto vacío
Un conjunto vacío es un conjunto que no tiene ningún elemento. Se representa con el símbolo "Ø" o con dos llaves sin nada dentro: "{ }". Como un conjunto está definido por sus elementos, solo puede haber un conjunto vacío.
Cómo se describen los conjuntos
Hay varias maneras de describir un conjunto:
- Enumerando sus elementos: La forma más sencilla es listar todos sus elementos entre llaves. Por ejemplo, {1, 2} es el conjunto que solo tiene los números 1 y 2.
* El orden de los elementos no importa: {{{1}}}. * Si un elemento se repite, no cambia el conjunto: {{{1}}}. * El conjunto vacío se escribe como {}.
- Usando una característica (notación constructora de conjuntos): Se usa la notación {x : P(x)} o {x | P(x)}. Esto significa "el conjunto de todos los x para los que la característica P es verdadera".
* Por ejemplo, {x : x es un número real} es el conjunto de todos los números reales. * También se puede especificar un conjunto a partir de otro: {x ∈ A : P(x)} significa "todos los x que ya están en A y que cumplen la característica P". Si Z es el conjunto de los enteros, entonces {x ∈ Z : x es par} es el conjunto de todos los enteros pares. * Otra forma es {F(x) : x ∈ A}, que significa "el conjunto de todos los resultados de aplicar la fórmula F a los elementos de A". Por ejemplo, {2x : x ∈ Z} es el conjunto de todos los enteros pares.
Subconjuntos
Un conjunto A es un subconjunto de otro conjunto B si cada elemento de A también es un elemento de B.
- Cada conjunto es un subconjunto de sí mismo.
- Un subconjunto que no es igual al conjunto original se llama subconjunto propio.
Si A es un subconjunto de B, también podemos decir que B es un superconjunto de A. Esto se escribe así: A ⊆ B (A es subconjunto de B) o B ⊇ A (B es superconjunto de A).
Por ejemplo, si R es el conjunto de los números reales, Z es el conjunto de los números enteros, y O es el conjunto de los números enteros impares:
- O es un subconjunto de Z.
- Z es un subconjunto de R.
- Por lo tanto, O también es un subconjunto de R.
No todos los conjuntos se pueden comparar así. Por ejemplo, el conjunto de los números reales no es un subconjunto del conjunto de los Presidentes de los Estados Unidos, y viceversa.
Una forma de probar que dos conjuntos A y B son iguales es demostrar que A ⊆ B y que B ⊆ A.
El conjunto vacío es un subconjunto de cualquier conjunto.
El conjunto de todos los subconjuntos de un conjunto A se llama conjunto potencia de A y se escribe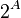 
o Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): P(A) . Si un conjunto A tiene n elementos, su conjunto potencia tendrá 
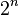elementos.
Conjuntos universales y complementos
En algunos casos, podemos considerar que todos los conjuntos con los que estamos trabajando son subconjuntos de un conjunto universal más grande. Por ejemplo, si estudiamos los números reales, el conjunto de todos los números reales (R) puede ser nuestro conjunto universal.
Dado un conjunto universal U y un subconjunto A de U, el complemento de A (en U) es el conjunto de todos los elementos de U que no están en A. Se escribe AC.
Por ejemplo, si Z (los enteros) es el conjunto universal y O (los enteros impares) es el conjunto A, entonces OC es el conjunto de los números enteros pares.
Uniones, intersecciones y diferencias
Dadas dos conjuntos A y B:
- La unión de A y B es el conjunto que contiene todos los objetos que están en A, o en B, o en ambos. Se escribe A ∪ B.
* Simbólicamente: A ∪ B := {x : (x ∈ A) o (x ∈ B)}.
- La intersección de A y B es el conjunto de todos los objetos que están tanto en A como en B. Se escribe A ∩ B.
* Simbólicamente: A ∩ B := {x : (x ∈ A) y (x ∈ B)}.
- El complemento relativo de B con respecto a A (también llamado diferencia de A y B) es el conjunto de todos los objetos que están en A pero no en B. Se escribe A \ B o A - B.
* Simbólicamente: A \ B := {x : (x ∈ A) y no (x ∈ B)}.
Para entenderlo mejor:
- Si A es el conjunto de personas zurdas y B es el conjunto de personas rubias:
* A ∩ B es el conjunto de personas zurdas y rubias. * A ∪ B es el conjunto de personas que son zurdas, o rubias, o ambas. * A \ B es el conjunto de personas zurdas que no son rubias. * B \ A es el conjunto de personas rubias que no son zurdas.
- Si E es el conjunto de todos los seres humanos y F es el conjunto de todos los seres vivos de más de 1000 años. ¿Cuál es E ∩ F? Como ningún ser humano vive más de 1000 años, la intersección es el conjunto vacío {}.
