Números pares e impares para niños
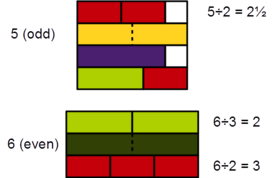
En matemáticas, un número par es un número entero que se puede dividir exactamente entre dos. Esto significa que, al dividirlo por 2, el resultado es otro número entero y no queda ningún resto. Los números pares se pueden escribir como 2k, donde k es cualquier número entero (positivo, negativo o cero).
Los números enteros que no son pares se llaman números impares. Estos no se pueden dividir exactamente entre dos, siempre dejan un resto de 1. Los números impares se pueden escribir como 2k+1.
Aquí tienes algunos ejemplos:
- Números pares: ..., -6, -4, -2, 0, 2, 4, 6, ...
- Números impares: ..., -5, -3, -1, 1, 3, 5, 7, ...
La paridad de un número entero se refiere a si es par o impar. Dos números tienen la "misma paridad" si ambos son pares o ambos son impares. Por ejemplo, 4 y 8 tienen la misma paridad (ambos son pares). 3 y 7 también tienen la misma paridad (ambos son impares). En cambio, 10 y 15 tienen "distinta paridad" porque uno es par y el otro es impar.
Contenido
Reglas básicas de la paridad
La paridad de los números sigue algunas reglas sencillas al sumarlos, restarlos o multiplicarlos:
- Par + Par = Par (Ejemplo: 2 + 4 = 6)
- Par + Impar = Impar (Ejemplo: 2 + 3 = 5)
- Impar + Impar = Par (Ejemplo: 3 + 5 = 8)
- Par - Par = Par (Ejemplo: 6 - 2 = 4)
- Par - Impar = Impar (Ejemplo: 6 - 3 = 3)
- Impar - Impar = Par (Ejemplo: 7 - 3 = 4)
- Par × Par = Par (Ejemplo: 2 × 4 = 8)
- Par × Impar = Par (Ejemplo: 2 × 3 = 6)
- Impar × Impar = Impar (Ejemplo: 3 × 5 = 15)
¿Cómo reconocer un número par?
Si un número está escrito en un sistema de numeración con una base par (como la base 10, que usamos normalmente, o la base 8), puedes saber si es par o impar mirando solo su último dígito.
- Un número es par si su último dígito es par (0, 2, 4, 6, 8).
* Por ejemplo, el número 352.107.706 es par porque su último dígito es 6, que es un número par.
- Un número es impar si su último dígito es impar (1, 3, 5, 7, 9).
* Por ejemplo, el número 123.457 es impar porque su último dígito es 7, que es un número impar.
Si la base del sistema de numeración es impar (como la base 3 o la base 5), la regla es diferente:
- Un número es par si la cantidad de dígitos impares que tiene es par.
* Por ejemplo, en base 5, el número 321 (que es 86 en base 10) es par. Sus dígitos impares son 3 y 1. Como hay dos dígitos impares (un número par), el número es par.
- Un número es impar si la cantidad de dígitos impares que tiene es impar.
* Por ejemplo, en base 3, el número 120 (que es 15 en base 10) es impar. Su único dígito impar es 1. Como hay un solo dígito impar (un número impar), el número es impar.
La paridad del cero
El número cero (0) es un número par. Cumple con todas las reglas y propiedades de los números pares. Por ejemplo, se puede dividir entre 2 y el resultado es 0, que es un número entero. Además, si sumas o restas 0 a un número, su paridad no cambia.
Propiedades de los números pares e impares
- Dos números enteros que están uno al lado del otro (consecutivos) siempre tienen paridades diferentes. Por ejemplo, 5 (impar) y 6 (par).
- Si tomas tres números enteros consecutivos, siempre habrá dos con la misma paridad y uno con una paridad diferente. Por ejemplo, 4 (par), 5 (impar), 6 (par). Aquí, 4 y 6 son pares, y 5 es impar.
Números especiales y su paridad
- El número 2 es el único número primo que es par. Todos los demás números primos son impares (como 3, 5, 7, 11, etc.).
- Los números perfectos son siempre pares. Un número perfecto es aquel que es igual a la suma de sus divisores propios (sin incluirse a sí mismo). Por ejemplo, 6 es un número perfecto porque sus divisores propios son 1, 2 y 3, y 1+2+3=6.
- Los factoriales de números naturales (excepto 0! y 1!) son siempre pares. El factorial de un número es el producto de todos los enteros positivos desde 1 hasta ese número. Por ejemplo, 4! = 1 × 2 × 3 × 4 = 24, que es par.
Paridad de las potencias
- Un número es par si y solo si su cuadrado (el número multiplicado por sí mismo) es un número par. Por ejemplo, 4 es par, y 4² = 16, que también es par.
- Un número es impar si y solo si su cuadrado es un número impar. Por ejemplo, 3 es impar, y 3² = 9, que también es impar.
Galería de imágenes
Véase también
 En inglés: Parity (mathematics) Facts for Kids
En inglés: Parity (mathematics) Facts for Kids