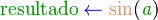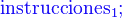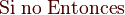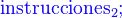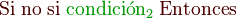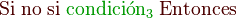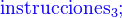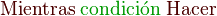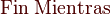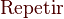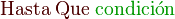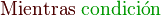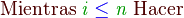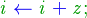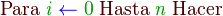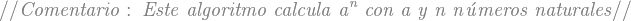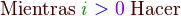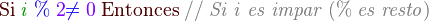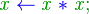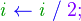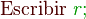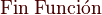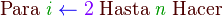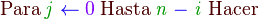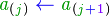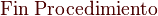Seudocódigo para niños

Enciclopedia para niños

En ciencias de la computación, y análisis numérico, el seudocódigo (o lenguaje de descripción algorítmico) es una descripción de alto nivel compacta e informal del principio operativo de un programa informático u otro algoritmo.

Utiliza las convenciones estructurales de un lenguaje de programación real, pero está diseñado para la lectura humana en lugar de la lectura mediante máquina, y con independencia de cualquier otro lenguaje de programación. Normalmente, el seudocódigo omite detalles que no son esenciales para la comprensión humana del algoritmo, tales como declaraciones de variables, código específico del sistema y algunas subrutinas. El lenguaje de programación se complementa, donde sea conveniente, con descripciones detalladas en lenguaje natural, o con notación matemática compacta. Se utiliza seudocódigo pues este es más fácil de entender para las personas que el código del lenguaje de programación convencional, ya que es una descripción eficiente y con un entorno independiente de los principios fundamentales de un algoritmo. Se utiliza comúnmente en los libros de texto y publicaciones científicas que se documentan varios algoritmos, y también en la planificación del desarrollo de programas informáticos, para esbozar la estructura del programa antes de realizar la efectiva codificación. Es comúnmente utilizado por los programadores para omitir secciones de Código o para dar una explicación del paradigma que tomó el mismo programador para hacer sus códigos, esto quiere decir que el seudocódigo no es programable, sino facilita la programación.

El principal objetivo del seudocódigo es el de representar la solución a un algoritmo de la forma más detallada posible, y a su vez lo más parecida posible al lenguaje que posteriormente se utilizará para la codificación del mismo.

No existe una sintaxis estándar para el seudocódigo, aunque los cinco IDE's que manejan seudocódigo en español tengan su sintaxis propia. Aunque sea parecido, el seudocódigo no debe confundirse con los programas esqueleto que incluyen código ficticio, que pueden ser compilados sin errores. Los diagramas de flujo y UML pueden ser considerados como una alternativa gráfica al seudocódigo, aunque sean más amplios

Aplicaciones

Generalmente se utiliza seudocódigo en los libros de texto y publicaciones científicas relacionadas con la informática y la computación numérica, para la descripción de algoritmos, de manera que todos los programadores puedan entenderlo, aunque no todos conozcan el mismo lenguaje de programación. Generalmente, en los libros de texto se adjunta una explicación que acompaña a la introducción y que explica las convenciones particulares en uso. El nivel de detalle del seudocientífico puede, en algunos casos, acercarse a la de formalizar los idiomas de propósito general.

Un programador que tiene que aplicar un algoritmo específico, sobre todo uno desfamiliarizado, generalmente comienza con una descripción en seudocódigo, y luego "traduce" esa descripción en el lenguaje de programación meta y lo modifica para que interactúe correctamente con el resto del programa. Los programadores también pueden iniciar un proyecto describiendo la forma del código en seudocódigo en el papel antes de escribirlo en su lenguaje de programación, como ocurre en la estructuración de un enfoque de Top-down y Bottom-up arriba hacia abajo.

Sintaxis

En la actualidad y por lo general, el seudocódigo, como su nombre lo indica, no obedece a las reglas de sintaxis de ningún idioma en particular ni es de forma estándar sistemática, a pesar de que cualquier escritor en particular vaya a pedir prestado las estructuras de control general, la sintaxis y el estilo, por ejemplo, de algún lenguaje de programación convencional. Pero en caso de que se quiera ejecutar, se debe llevar a forma tipo, para que no genere mensajes de error. Las fuentes populares incluyen la sintaxis de Pascal, BASIC, C, C++, Java, Lisp, y ALGOL. Por lo general, se omiten las declaraciones de variables. A veces, las llamadas a funciones, los bloques de código y el código contenido dentro de un loop se remplazan por una sentencia de una línea en lenguaje natural.

Este es un ejemplo de seudocódigo (para el juego matemático bizz buzz):

Seudocódigo estilo Fortran: programa bizzbuzz hacer i = 1 hasta 100 establecer print_number a verdadero si i es divisible por 3 escribir "Bizz" establecer print_number a falso si i es divisible por 5 escribir "Buzz" establecer print_number a falso si print_number, escribir i escribir una nueva línea fin del hacer	Seudocódigo estilo Pascal: procedimiento bizzbuzz para i := 1 hasta 100 hacer establecer print_number a verdadero; Si i es divisible por 3 entonces escribir "Bizz"; establecer print_number a falso; Si i es divisible por 5 entonces escribir "Buzz"; establecer print_number a falso; Si print_number, escribir i; escribir una nueva línea; fin	Seudocódigo estilo C: subproceso funcion bizzbuzz para (i <- 1; i<=100; i++) { establecer print_number a verdadero; Si i es divisible por 3 escribir "Bizz"; establecer print_number a falso; Si i es divisible por 5 escribir "Buzz"; establecer print_number a falso; Si print_number, escribir i; escribir una nueva línea; }

Seudocódigo estilo Fortran:

programa bizzbuzz
hacer i = 1 hasta 100
    establecer print_number a verdadero
    si i es divisible por 3
        escribir "Bizz"
        establecer print_number a falso
    si i es divisible por 5
        escribir "Buzz"
        establecer print_number a falso
    si print_number, escribir i
    escribir una nueva línea
fin del hacer

Seudocódigo estilo Pascal:

procedimiento bizzbuzz
para i := 1 hasta 100 hacer
    establecer print_number a verdadero;
    Si i es divisible por 3 entonces
        escribir "Bizz";
        establecer print_number a falso;
    Si i es divisible por 5 entonces
        escribir "Buzz";
        establecer print_number a falso;
    Si print_number, escribir i;
    escribir una nueva línea;
fin

Seudocódigo estilo C:

subproceso funcion bizzbuzz
para (i <- 1; i<=100; i++) {
    establecer print_number a verdadero;
    Si i es divisible por 3
        escribir "Bizz";
        establecer print_number a falso;
    Si i es divisible por 5
        escribir "Buzz";
        establecer print_number a falso;
    Si print_number, escribir i;
    escribir una nueva línea;
}

Definición de datos en seudocódigo

La definición de datos se da por supuesta, sobre todo en las variables sencillas, si se emplea formaciones: pilas, colas, vectores o registros, se pueden definir en la cabecera del algoritmo, y naturalmente cuando empleemos el seudocódigo para definir estructuras de datos, esta parte la desarrollaremos adecuadamente.

Funciones y operaciones

Cada autor usa su propio seudocódigo con sus respectivas convenciones. Por ejemplo, la instrucción "reemplace el valor de la variable $x$ por el valor de la variable $y$ " puede ser representado como:

asigne a 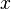$x\,$ el valor de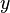 $y\,$

${ \color{OliveGreen} \mathit{ x }} \; { \color{BlueViolet} \mathit{ \gets }} \; { \color{OliveGreen} \mathit{ y; }}$

${ \color{OliveGreen} \mathit{ x }} \; { \color{BlueViolet} \mathit{ := }} \; { \color{OliveGreen} \mathit{ y; }}$

${ \color{OliveGreen} \mathit{ x }} \; { \color{BlueViolet} \mathit{ = }} \; { \color{OliveGreen} \mathit{ y; }}$

Las operaciones aritméticas se representan de la forma usual en matemáticas.

${ \color{Gray} \mathit{ \{ Esto \; es \; un \; comentario \; normalmente \; matem \acute{a} tico \} }}$

Error al representar (La conversión a PNG ha fallado; comprueba que latex, dvips, gs, y convert estén instalados correctamente): { \color{OliveGreen} \mathrm{ volumen }} \; { \color{BlueViolet} \mathit{ \gets }} \; { \color{Red} \mathit{ \pi }} { \color{Oliveblack} \mathit{ r }} {}^2 { \color{OliveGreen} \mathit{ h }}

${ \color{Gray} \mathit{ // y \; este \; es \; otro \; comentario \; normalmente \; de \; texto // }}$

${ \color{OliveGreen} \mathrm{ hipotenusa }} \; { \color{BlueViolet} \mathrm{ \gets }} \; \sqrt{ { \color{OliveGreen} \mathit{ a }} {}^2 \; { \color{BlueViolet} \mathit{ + }} \; { \color{OliveGreen} \mathit{ b }} {}^2 \; }$

${ \color{OliveGreen} \mathrm{ resultado }} \; { \color{BlueViolet} \mathit{ \gets }} \; { \color{Tan} \mathrm{ sin }} ( { \color{OliveGreen} \mathit{ a }} )$

Estructuras de control

En la redacción de seudocódigo se utiliza tres tipos de estructuras de control: las secuenciales, las selectivas y las iterativas.

Estructuras secuenciales

Las instrucciones se siguen en una secuencia fija que normalmente viene dada por el número de renglón. Es decir que las instrucciones se ejecutan de arriba hacia abajo.

${ \color{BlueViolet} \mathrm{ instrucci \acute{o} n_1; }}$

${ \color{BlueViolet} \mathrm{ instrucci \acute{o} n_2; }}$

${ \color{BlueViolet} \mathrm{ instrucci \acute{o} n_3; }}$

$\cdots$

${ \color{BlueViolet} \mathrm{ instrucci \acute{o} n_{\it n}; }}$

Estructuras selectivas

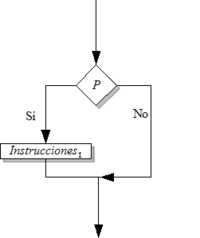
Las instrucciones selectivas representan instrucciones que pueden o no ejecutarse, según el cumplimiento de una condición.

Diagrama de flujo que muestra el funcionamiento de la instrucción condicional.

${ \color{Sepia} \mathrm{ Si }} \; { \color{OliveGreen} \mathrm{ condici \acute{o} n }} \; { \color{Sepia} \mathrm{ Entonces }}$

${ \color{BlueViolet} \mathrm{ instrucciones; }}$

${ \color{Sepia} \mathrm{ Fin \; Si }}$

La condición es una expresión booleana. Instrucciones es ejecutada solo si la condición es verdadera.

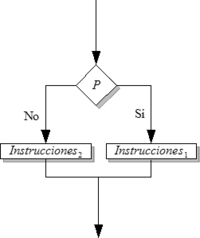
Selectiva doble (alternativa)

La instrucción alternativa realiza una instrucción de dos posibles, según el cumplimiento de una condición.

Diagrama de flujo que muestra el funcionamiento de la instrucción condicional.

${ \color{Sepia} \mathrm{ Si }} \; { \color{OliveGreen} \mathrm{ condici \acute{o} n }} \; { \color{Sepia} \mathrm{ Entonces }}$

${ \color{BlueViolet} \mathrm{ instrucciones_1; }}$

${ \color{Sepia} \mathrm{ Si \; no \; Entonces }}$

${ \color{BlueViolet} \mathrm{ instrucciones_2; }}$

${ \color{Sepia} \mathrm{ Fin \; Si }}$

La condición es una variable booleana o una función reducible a booleana (lógica, Verdadero/Falso). Si esta condición es cierta se ejecuta Instrucciones₁, si no es así, entonces se ejecuta Instrucciones₂.

Selectiva múltiple

También es común el uso de una selección múltiple que equivaldría a anidar varias funciones de selección.

${ \color{Sepia} \mathrm{ Si }} \; { \color{OliveGreen} \mathrm{ condici \acute{o} n_1 }} \; { \color{Sepia} \mathrm{ Entonces }}$

${ \color{BlueViolet} \mathrm{ instrucciones_1; }}$

${ \color{Sepia} \mathrm{ Si \; no \; si }} \; { \color{OliveGreen} \mathrm{ condici \acute{o} n_2 }} \; { \color{Sepia} \mathrm{ Entonces }}$

${ \color{BlueViolet} \mathrm{ instrucciones_2; }}$

${ \color{Sepia} \mathrm{ Si \; no \; si }} \; { \color{OliveGreen} \mathrm{ condici \acute{o} n_3 }} \; { \color{Sepia} \mathrm{ Entonces }}$

${ \color{BlueViolet} \mathrm{ instrucciones_3; }}$

$\cdots$

${ \color{Sepia} \mathrm{ Si \; no \; Entonces }}$

${ \color{BlueViolet} \mathrm{ instrucciones_{\it n}; }}$

${ \color{Sepia} \mathrm{ Fin \; Si }}$

En este caso hay una serie de condiciones que tienen que ser mutuamente excluyentes, si una de ellas se cumple las demás tienen que ser falsas necesariamente, hay un caso si no que será cierto cuando las demás condiciones sean falsas.

En esta estructura si Condición₁ es cierta, entonces se ejecuta solo Instrucciones₁. En general, si Condición_i es verdadera, entonces solo se ejecuta Instrucciones_i

Selectiva múltiple-Casos

Una construcción similar a la anterior (equivalente en algunos casos) es la que se muestra a continuación.

${ \color{Sepia} \mathrm{ Seg\acute{u}n }} \; { \color{OliveGreen} \mathrm{ variable }} \; { \color{Sepia} \mathrm{ Hacer }}$

${ \color{Sepia} \mathrm{ caso }} \; { \color{OliveGreen} \mathrm{ valor_1; }}$

${ \color{BlueViolet} \mathrm{ instrucciones_1; }}$

${ \color{Sepia} \mathrm{ caso }} \; { \color{OliveGreen} \mathrm{ valor_2; }}$

${ \color{BlueViolet} \mathrm{ instrucciones_2; }}$

${ \color{Sepia} \mathrm{ caso }} \; { \color{OliveGreen} \mathrm{ valor_3; }}$

${ \color{BlueViolet} \mathrm{ instrucciones_3; }}$

$\cdots$

${ \color{Sepia} \mathrm{ De \; Otro \; Modo}}$

${ \color{BlueViolet} \mathrm{ instrucciones_{\it n}; }}$

${ \color{Sepia} \mathrm{ Fin \; Seg\acute{u}n }}$

En este caso hay un Indicador es una variable o una función cuyo valor es comparado en cada caso con los valores "Valor_i", si en algún caso coinciden ambos valores, entonces se ejecutarán las Instrucciones_i correspondientes. La sección en otro caso es análoga a la sección si no del ejemplo anterior.

Estructuras iterativas

Las instrucciones iterativas representan la ejecución de instrucciones en más de una vez.

Bucle mientras

Artículo principal: Bucle while

El bucle se repite mientras la condición sea cierta, si al llegar por primera vez al bucle mientras la condición es falsa, el cuerpo del bucle no se ejecuta alguna vez.

Diagrama de flujo que muestra el funcionamiento de la instrucción mientras

${ \color{Sepia} \mathrm{ Mientras }} \; { \color{OliveGreen} \mathrm{ condici \acute{o} n }} \; { \color{Sepia} \mathrm{ Hacer }}$

${ \color{BlueViolet} \mathrm{ instrucciones; }}$

${ \color{Sepia} \mathrm{ Fin \; Mientras }}$

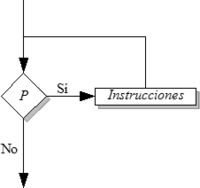
Bucle repetir

Existen otras variantes que se derivan a partir de la anterior. La estructura de control repetir se utiliza cuando es necesario que el cuerpo del bucle se ejecuten al menos una vez y hasta que se cumpla la condición:

${ \color{Sepia} \mathrm{ Repetir }}$

${ \color{BlueViolet} \mathrm{ instrucciones; }}$

${ \color{Sepia} \mathrm{ Hasta \; Que }} \; { \color{OliveGreen} \mathrm{ condici \acute{o} n }}$

La estructura anterior equivaldría a escribir:

${ \color{BlueViolet} \mathrm{ instrucciones; }}$

${ \color{Sepia} \mathrm{ Mientras }} \; { \color{BlueViolet} \mathrm{ \neg }} ( { \color{OliveGreen} \mathrm{ condici \acute{o} n }} ) \; { \color{Sepia} \mathrm{ Hacer }}$

${ \color{BlueViolet} \mathrm{ instrucciones; }}$

${ \color{Sepia} \mathrm{ Fin \; Mientras }}$

Bucle hacer

El Bucle hacer se utiliza para repetir un bloque de código mientras se cumpla cierta condición.

${\color{Sepia} \mathrm{ Hacer }} \;$

${\color{BlueViolet} \mathrm{ instrucciones; }} \;$

${\color{Sepia} \mathrm{ Mientras}} \; {\color{OliveGreen} \mathrm{ condici \acute{o} n }}$

Bucle para

Artículo principal: Bucle for

Una estructura de control muy común es el ciclo FOR, la cual se usa cuando se desea iterar un número conocido de veces, empleando como índice una variable que se incrementa (o decrementa):

${ \color{Sepia} \mathrm{ Para }} \; { \color{OliveGreen} \mathit{ i }} \; { \color{BlueViolet} \mathit{ \gets }} \; { \color{OliveGreen} \mathit{ x }} \; { \color{Sepia} \mathrm{ Hasta }} \; { \color{OliveGreen} \mathit{ n }} \; { \color{Sepia} \mathrm{ Con \; Paso }} \; { \color{OliveGreen} \mathit{ z}} \; { \color{Sepia} \mathrm{ Hacer }}$

${ \color{BlueViolet} \mathrm{ instrucciones; }}$

${ \color{Sepia} \mathrm{ Fin \; Para }}$

la cual se define como:

${ \color{OliveGreen} \mathit{ i}} \; { \color{BlueViolet} \mathrm{ \gets }} \; { \color{OliveGreen} \mathit{ x}}$

${ \color{Sepia} \mathrm{ Mientras }} \; { \color{OliveGreen} \mathit{ i }} \; { \color{BlueViolet} \mathit{ \leq }} \; { \color{OliveGreen} \mathit{ n }} \; { \color{Sepia} \mathrm{ Hacer }}$

${ \color{BlueViolet} \mathrm{ instrucciones; }}$

${ \color{OliveGreen} \mathit{ i }} \; { \color{BlueViolet} \mathrm{ \gets }} \; { \color{OliveGreen} \mathit{ i }} \; { \color{BlueViolet} \mathrm{ + }} \; { \color{OliveGreen} \mathit{ z; }}$

${ \color{Sepia} \mathrm{ Fin \; Mientras }}$

Bucle para cada

Por último, también es común usar la estructura de control para cada. Esta sentencia se usa cuando se tiene una lista o un conjunto 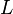$L$ y se quiere iterar por cada uno de sus elementos:

${ \color{Sepia} \mathrm{ Para \; Cada }} \; { \color{OliveGreen} \mathit{ x }} \; { \color{BlueViolet} \mathit{ \in }} \; { \color{OliveGreen} \mathit{ L }} \; { \color{Sepia} \mathrm{ Hacer }}$

${ \color{BlueViolet} \mathrm{ instrucciones; }}$

${ \color{Sepia} \mathrm{ Fin \; Para \; Cada }}$

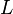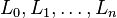Si asumimos que los elementos de $L$ son $L_0,L_1,\dots,L_n$ , entonces esta sentencia equivaldría a:

${ \color{Sepia} \mathrm{ Para }} \; { \color{OliveGreen} \mathit{ i}} \; { \color{BlueViolet} \mathit{ \gets }} \; { \color{OliveGreen} \mathrm{ 0}} \; { \color{Sepia} \mathrm{ Hasta }} \; { \color{OliveGreen} \mathit{ n}} \; { \color{Sepia} \mathrm{ Con \; Paso }} \; { \color{OliveGreen} \mathrm{ 1}} \; { \color{Sepia} \mathrm{ Hacer }}$

${ \color{OliveGreen} \mathit{ x }} \; { \color{BlueViolet} \mathit{ \gets}} \; { \color{OliveGreen} \mathit{ L_i }}$

${ \color{BlueViolet} \mathrm{ instrucciones; }}$

${ \color{Sepia} \mathrm{ Fin \; Para }}$

Que es lo mismo que:

${ \color{Sepia} \mathrm{ Para }} \; { \color{OliveGreen} \mathit{ i}} \; { \color{BlueViolet} \mathit{ \gets }} \; { \color{OliveGreen} \mathrm{ 0}} \; { \color{Sepia} \mathrm{ Hasta }} \; { \color{OliveGreen} \mathit{ n}} \; { \color{Sepia} \mathrm{ Hacer }}$

${ \color{OliveGreen} \mathit{ x }} \; { \color{BlueViolet} \mathit{ \gets}} \; { \color{OliveGreen} \mathit{ L_i }}$

${ \color{BlueViolet} \mathrm{ instrucciones; }}$

${ \color{Sepia} \mathrm{ Fin \; Para }}$

Sin embargo, en la práctica existen mejores formas de implementar esta instrucción dependiendo del problema.

Es importante recalcar que el seudocódigo no es un lenguaje estandarizado. Eso significa que diferentes autores podrían dar otras estructuras de control o bien usar estas mismas estructuras, pero con una notación diferente. Sin embargo, las funciones matemáticas y lógicas toman el significado usual que tienen en matemática y lógica, con las mismas expresiones.

El anidamiento

Cualquier instrucción puede ser sustituida por una estructura de control. El siguiente ejemplo muestra el seudocódigo del ordenamiento de burbuja, que tiene varias estructuras anidadas. Este algoritmo ordena de menor a mayor los elementos de una lista 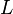$L$ .

Error al representar (La conversión a PNG ha fallado; comprueba que latex, dvips, gs, y convert estén instalados correctamente): \begin{array}{l} { \color{Sepia} \mathrm{Procedimiento} } \; { \color{BlueViolet} \mathrm{Ordenar} } \; ( { \color{OliveGreen} L} \; ) \\ \left \updownarrow \begin{array}{l} { \color{Gray} // Comentario: \; L=(L_1,L_2,\dots,L_n) \; es \; una \; lista \; con \; n \; elementos // } \\ { \color{OliveGreen} k } \; { \color{BlueViolet} \gets } \; { \color{OliveGreen} 0;} \\ { \color{Sepia} \mathrm{Repetir} } \\ \left \updownarrow \begin{array}{l} { \color{OliveGreen} \mathrm{intercambio} } \; { \color{BlueViolet} \gets } \; { \color{OliveGreen} \mathrm{Falso};} \\ { \color{OliveGreen} k } \; { \color{BlueViolet} \gets } \; { \color{OliveGreen} k + 1;} \\ { \color{Sepia} \mathrm{Para} } \; { \color{OliveGreen} i} \; { \color{BlueViolet} \gets } \; { \color{OliveGreen} 1} \; { \color{Sepia} \mathrm{Hasta} } \; { \color{OliveGreen} n - k} \; { \color{Sepia} \mathrm{Con \; Paso} } \; { \color{OliveGreen} 1} \; { \color{Sepia} \mathrm{Hacer} } \\ \left \updownarrow \begin{array}{l} { \color{Sepia} \mathrm{Si} } \; { \color{OliveGreen} L_i } \; { \color{BlueViolet} > } \; { \color{OliveGreen} L_{i+1} } \; { \color{Sepia} \mathrm{Entonces} } \; \\ \left \updownarrow \begin{array}{l} { \color{BlueViolet} \mathrm{intercambiar} } \; ( { \color{OliveGreen} L_i , L_{i+1} } \; ) \\ { \color{OliveGreen} \mathrm{intercambio} } \; { \color{BlueViolet} \gets } \; { \color{OliveGreen} \mathrm{Verdadero};} \end{array} \right . \\ { \color{Sepia} \mathrm{Fin \; Si} } \; \\ \end{array} \right . \\ { \color{Sepia} \mathrm{Fin \; Para} } \\ \end{array} \right . \\ { \color{Sepia} \mathrm{Hasta \; Que} } \; { \color{OliveGreen} \mathrm{intercambio} } \; { \color{bluet} = } \; { \color{OliveGreen} \mathrm{Falso};} \end{array} \right . \\ { \color{Sepia} \mathrm{Fin \; Procedimiento} } \; \\ \end{array}

En general, las estructuras anidadas se muestran indentadas, para hacer más sencilla su identificación a simple vista. En el ejemplo, además de la sangría, se ha conectado con flechas los pares de delimitadores de cada nivel de anidamiento.

Funciones y procedimientos

Muchas personas prefieren distinguir entre funciones y procedimientos. Una función, al igual que una función matemática, recibe uno o varios valores de entrada y regresa una salida mientras que un procedimiento recibe una entrada y no genera alguna salida aunque en algún caso podría devolver resultados a través de sus parámetros de entrada si estos se han declarado por referencia (ver formas de pasar argumentos a una función o procedimiento).

En ambos casos es necesario dejar en claro cuáles son las entradas para el algoritmo, esto se hace comúnmente colocando estos valores entre paréntesis al principio o bien declarándolo explícitamente con un enunciado. En el caso de las funciones, es necesario colocar una palabra como regresar o devolver para indicar cuál es la salida generada por el algoritmo. Por ejemplo, el seudocódigo de una función que permite calcular 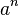$a^n$ (un número $a$ elevado a potencia $n$ ).

${ \color{Sepia} \mathrm{ Funci \acute{o} n }} \; { \color{BlueViolet} \mathrm{ potencia }} \; ( { \color{OliveGreen} \mathit{ a,n}} )$

${ \color{Gray} \mathit{ // Comentario: \; Este \; algoritmo \; calcula \; a^n \; con \; a \; y \; n \; n \acute{u} meros \; naturales // }}$

${ \color{OliveGreen} \mathit{ i }} \; { \color{BlueViolet} \mathit{ \gets }} \; { \color{OliveGreen} \mathit{ n; }}$

${ \color{OliveGreen} \mathit{ r }} \; { \color{BlueViolet} \mathit{ \gets }} \; { \color{Plum} \mathrm{ 1;}}$

${ \color{OliveGreen} \mathit{ x }} \; { \color{BlueViolet} \mathit{ \gets }} \; { \color{OliveGreen} \mathit{ a; }}$

${ \color{Sepia} \mathrm{ Mientras }} \; { \color{OliveGreen} \mathit{ i }} \; { \color{BlueViolet} \mathit{ > }} \; { \color{Plum} \mathrm{ 0 }} \; { \color{Sepia} \mathrm{ Hacer }}$

${ \color{Sepia} \mathrm{ Si }} \; { \color{OliveGreen} \mathit{ i }} \; { \color{BlueViolet} \mathit{ \% }} \; { \color{Plum} \mathrm{ 2}} { \color{BlueViolet} \mathit{ \neq }} \; { \color{Plum} \mathrm{ 0}} \; { \color{Sepia} \mathrm{ Entonces }} \; { \color{Gray} \mathit{ //\; Si \; i \; es \; impar \; (\% \; es \; resto)}}$

${ \color{OliveGreen} \mathit{ r }} \; { \color{BlueViolet} \mathit{ \gets }} \; { \color{OliveGreen} \mathit{ r }} \; { \color{BlueViolet} \mathit{ * }} \; { \color{OliveGreen} \mathit{ x; }}$

${ \color{Sepia} \mathrm{ Fin \; Si }}$

${ \color{OliveGreen} \mathit{ x }} \; { \color{BlueViolet} \mathit{ \gets }} \; { \color{OliveGreen} \mathit{ x }} \; { \color{BlueViolet} \mathit{ * }} \; { \color{OliveGreen} \mathit{ x; }}$

${ \color{OliveGreen} \mathit{ i }} \; { \color{BlueViolet} \mathit{ \gets }} \; { \color{OliveGreen} \mathit{ i }} \; { \color{BlueViolet} \mathit{ / }} \; { \color{Plum} \mathrm{ 2; }} \;$

${ \color{Sepia} \mathrm{ Fin \; Mientras }}$

${ \color{Sepia} \mathrm{ Escribir }} \; { \color{OliveGreen} \mathit{ r; }}$

${ \color{Sepia} \mathrm{ Fin \; Funci \acute{o} n }}$

Un ejemplo de procedimiento sería el algoritmo de ordenamiento de burbuja, por el que partiendo de una lista de valores estos se ordenan, nótese que en un procedimiento, no se calcula el valor de una función, sino que se realiza una acción, en este caso ordenar la lista.

${ \color{Sepia} \mathrm{ Procedimiento }} \; { \color{BlueViolet} \mathrm{ DeLaBurbuja }} \; ( { \color{OliveGreen} \mathit{ a }} { \color{Plum} \mathrm{ {}_0 }} , { \color{OliveGreen} \mathit{ a }} { \color{Plum} \mathrm{ {}_1 }} , { \color{OliveGreen} \mathit{ a }} { \color{Plum} \mathrm{ {}_2 }} , \ldots, { \color{OliveGreen} \mathrm{ a }} {}_( { \color{OliveGreen} \mathit{ {}_n }} { \color{BlueViolet} \mathit{ {}_- }} { \color{Plum} \mathrm{ {}_1}} {}_) )$

${ \color{Sepia} \mathrm{ Para }} \; { \color{OliveGreen} \mathit{ i}} \; { \color{BlueViolet} \mathit{ \gets }} \; { \color{Plum} \mathrm{ 2}} \; { \color{Sepia} \mathrm{ Hasta }} \; { \color{OliveGreen} \mathit{ n}} \; { \color{Sepia} \mathrm{ Hacer }}$

${ \color{Sepia} \mathrm{ Para }} \; { \color{OliveGreen} \mathit{ j}} \; { \color{BlueViolet} \mathit{ \gets }} \; { \color{Plum} \mathrm{ 0}} \; { \color{Sepia} \mathrm{ Hasta }} \; { \color{OliveGreen} \mathit{ n }} \; { \color{BlueViolet} \mathit{ - }} \; { \color{OliveGreen} \mathit{ i }} \; { \color{Sepia} \mathrm{ Hacer }}$

${ \color{Sepia} \mathrm{ Si }} \; { \color{OliveGreen} \mathit{ a }} {}_( { \color{OliveGreen} \mathit{ {}_j }} {}_) \; { \color{BlueViolet} \mathit{ < }} \; { \color{OliveGreen} \mathit{ a }} {}_( { \color{OliveGreen} \mathit{ {}_j }} { \color{BlueViolet} \mathit{ {}_+ }} { \color{Plum} \mathrm{ {}_1}} {}_) \; { \color{Sepia} \mathrm{ Entonces }}$

${ \color{OliveGreen} \mathrm{ aux }} \; { \color{BlueViolet} \mathit{ \gets }} \; { \color{OliveGreen} \mathit{ a }} {}_( { \color{OliveGreen} \mathit{ {}_j }} {}_) \;$

${ \color{OliveGreen} \mathit{ a }} {}_( { \color{OliveGreen} \mathit{ {}_j }} {}_) \; { \color{BlueViolet} \mathit{ \gets }} \; { \color{OliveGreen} \mathit{ a }} {}_( { \color{OliveGreen} \mathit{ {}_j }} { \color{BlueViolet} \mathit{ {}_+ }} { \color{Plum} \mathrm{ {}_1}} {}_)$

${ \color{OliveGreen} \mathit{ a }} {}_( { \color{OliveGreen} \mathit{ {}_j }} { \color{BlueViolet} \mathit{ {}_+ }} { \color{Plum} \mathrm{ {}_1}} {}_) \; { \color{BlueViolet} \mathit{ \gets }} \; { \color{OliveGreen} \mathrm{ aux }}$

${ \color{Sepia} \mathrm{ Fin \; Si }}$

${ \color{Sepia} \mathrm{ Fin \; Para }}$

${ \color{Sepia} \mathrm{ Fin \; Para }}$

${ \color{Sepia} \mathrm{ Fin \; Procedimiento }}$

Desarrollo de algoritmos

Con el seudocódigo se puede desarrollar cualquier algoritmo que:

Tenga un único punto de inicio.
Tenga un número finito de posibles puntos de término.
Halla un número finito de caminos, entre el punto de inicio y los posibles puntos de término.

Ventajas del seudocódigo sobre los diagramas de flujo

Los seudocódigos presentan los siguientes beneficios:

Ocupan mucho menos espacio en el desarrollo del problema.
Permite representar de forma fácil operaciones repetitivas complejas.
Es más sencilla la tarea de pasar de seudocódigo a un lenguaje de programación formal.
Si se siguen las reglas de sangría se puede observar claramente los niveles en la estructura del programa.
En los procesos de aprendizaje de los alumnos de programación, éstos están más cerca del paso siguiente (codificación en un lenguaje determinado, que los que se inician en esto con la modalidad Diagramas de Flujo).
Mejora la claridad de la solución de un problema.

Véase también

En inglés: Pseudocode Facts for Kids

PSeInt
Algoritmo
Programación
Resolución de problemas de programación
Diagrama de flujo
Estructuras de control

Bucle (programación)
Bucle for
Bucle do
Bucle while
Bucle repetir
Bucle infinito

Obtenido de «https://ninos.kiddle.co/index.php?title=Seudocódigo&oldid=4072612»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Seudocódigo para Niños. Enciclopedia Kiddle.