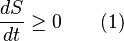Segundo principio de la termodinámica para niños
El segundo principio de la termodinámica es una regla fundamental de la física que nos ayuda a entender cómo funcionan los procesos naturales. Nos dice que la cantidad de entropía del universo siempre tiende a aumentar con el tiempo.
Este principio explica por qué muchos eventos en la naturaleza son "irreversibles", es decir, solo pueden ocurrir en una dirección. Por ejemplo, un vaso que se cae y se rompe no puede volver a unirse por sí solo. Fue propuesto por primera vez por Sadi Carnot en 1824 y luego desarrollado por otros científicos importantes como Rudolf Clausius, Lord Kelvin, Ludwig Boltzmann y Max Planck a lo largo del siglo XIX.
El segundo principio introduce el concepto de entropía, que podemos entender como una medida del desorden o la aleatoriedad en un sistema. En cualquier proceso real, la entropía de un sistema aislado siempre aumenta o se mantiene igual, nunca disminuye.
Contenido
¿Qué es el Segundo Principio de la Termodinámica?
El segundo principio de la termodinámica es una de las leyes más importantes de la física. Aunque se puede explicar de varias maneras, todas ellas nos llevan a comprender la idea de la irreversibilidad y el concepto de entropía.
Entropía: La Medida del Desorden
Cuando hablamos de entropía, especialmente en el campo de la mecánica estadística, nos referimos al grado de desorden de la materia y la energía en un sistema. Imagina tu habitación: si está muy ordenada, tiene poca entropía. Si está desordenada, tiene mucha entropía. La naturaleza tiende a ir de estados ordenados a estados más desordenados.
Por ejemplo, el agua en estado gaseoso (vapor) tiene más entropía que el agua líquida, porque sus moléculas están más dispersas y desordenadas. En cambio, en estado líquido, las moléculas están más juntas y ordenadas.
¿Cómo se Relaciona con el Primer Principio?
El primer principio de la termodinámica nos dice que la energía no se crea ni se destruye, solo se transforma. El segundo principio añade algo crucial: nos dice en qué dirección ocurren esas transformaciones. Sin embargo, es importante recordar que el segundo principio se aplica principalmente a sistemas que están en equilibrio o que se mueven hacia él.
Cuando un sistema pasa de un estado de equilibrio a otro, la cantidad de entropía en el nuevo estado será la máxima posible y siempre mayor que la del estado anterior. Esto significa que, en un sistema aislado, el desorden interno siempre aumenta.
El Destino del Universo y las Estrellas
Podemos aplicar este concepto a fenómenos naturales, como la vida de las estrellas. Las estrellas, como nuestro Sol, producen luz y calor al transformar hidrógeno en helio en su interior. Este proceso libera mucha energía. Sin embargo, cuando la estrella empieza a fusionar helio en elementos más pesados, no libera tanta energía. Con cada paso, la estrella usa un "combustible" que le es menos útil para producir energía. Finalmente, la estrella muere.
La materia que queda después de la muerte de una estrella ya no sirve para formar otra estrella de la misma manera. De esta forma, el segundo principio de la termodinámica se ha usado para explicar la idea de que el universo tiende hacia un estado de máximo desorden, donde ya no habrá energía útil para realizar procesos.
Entropía y su Definición Formal
La definición formal del segundo principio de la termodinámica dice que:
En un estado de equilibrio, los valores de las características de un sistema termodinámico aislado son tales que hacen que una magnitud llamada entropía sea lo más grande posible.
La entropía es una cantidad abstracta que, en la mecánica estadística, se relaciona con el nivel de desorden de las moléculas dentro de un sistema físico. En la termodinámica clásica, se define como la relación entre el calor transferido y la temperatura a la que se transfiere.
Los "parámetros característicos" de un sistema en equilibrio son su energía interna, su volumen y su composición. La entropía es una función de estos parámetros. El segundo principio establece que la entropía solo se puede definir para estados de equilibrio y que, de todos los estados posibles, el sistema siempre tenderá al que tenga la entropía más alta.
Esto significa que la entropía de un sistema aislado siempre aumenta. Si el universo comenzó en un estado de equilibrio y es un sistema aislado, entonces la cantidad de entropía del universo tiende a aumentar con el tiempo.
Matemáticamente, el cambio en la entropía (S) es siempre mayor o igual que la transferencia de calor (Q) dividida por la temperatura (T) del sistema:
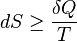 .
.
El signo de igualdad solo se da en procesos ideales y reversibles.
¿Por qué es tan Importante el Segundo Principio?

El segundo principio nos ayuda a distinguir qué procesos físicos son posibles y cuáles no. Por ejemplo, siempre vemos que para calentar algo, necesitamos una fuente de calor que esté a mayor temperatura. Nunca vemos que una caldera se caliente por sí sola tomando energía de su entorno y enfriándolo aún más. Esto es porque el calor siempre fluye de lo más caliente a lo más frío, nunca al revés de forma espontánea.
Esta ley fue muy importante durante la Revolución Industrial para entender cómo funcionaban las máquinas de vapor. Para que una máquina produzca trabajo, necesita combustible que aporte energía. La energía que se obtiene siempre es menor que la energía aportada, porque parte de ella se "pierde" como calor no utilizable, aumentando la entropía.
Enunciados Clásicos del Segundo Principio
El segundo principio se ha formulado de muchas maneras a lo largo de la historia. Aquí te presentamos algunas de las más conocidas:
- Enunciado de Clausius (1850): "Es imposible que una máquina que funciona por sí misma, sin ayuda externa, transfiera calor de un cuerpo frío a uno más caliente." Esto significa que un refrigerador, por ejemplo, necesita electricidad para funcionar, no puede enfriar las cosas por sí solo.
- Enunciado de Kelvin (1851): "Es imposible construir un dispositivo que, usando un fluido, pueda producir trabajo efectivo solo enfriando el cuerpo más frío disponible." Esto quiere decir que no podemos obtener energía útil de la nada, simplemente enfriando algo que ya está frío.
- Enunciado de Planck-Kelvin (1897): "Es imposible construir una máquina que funcione de forma regular y que solo haga una cosa: levantar un peso y, al mismo tiempo, enfriar una fuente de calor." Esto refuerza la idea de que siempre hay una "pérdida" de energía útil en forma de calor.
En resumen, el segundo principio nos dice que para que una máquina térmica funcione, siempre debe haber una diferencia de temperatura y siempre se necesitará energía adicional para producir trabajo útil.
Matemáticamente, la entropía (S) de un sistema aislado siempre aumenta o se mantiene igual:
El signo de igualdad solo se da cuando la entropía ya ha alcanzado su valor máximo, es decir, cuando el sistema está en equilibrio.
Entropía en la Mecánica Estadística
La termodinámica clásica no explica qué es la entropía a nivel físico, solo la define como una función matemática que alcanza su valor máximo en el equilibrio. Sin embargo, la mecánica estadística nos da una idea más clara: la entropía se relaciona con el número de formas en que las partículas de un sistema pueden organizarse.
Entropía y Microestados
Imagina un sistema con muchas partículas, como un gas en un recipiente. A nivel macroscópico (lo que podemos ver y medir), el gas tiene una cierta energía, volumen y cantidad de materia. Pero a nivel microscópico (los átomos y moléculas), estas partículas están en constante movimiento y pueden estar en muchísimos estados diferentes, llamados "microestados".
La mecánica estadística nos dice que un sistema macroscópico está cambiando muy rápidamente entre todos los microestados posibles. Como estos cambios son aleatorios, se asume que el sistema visita todos los microestados permitidos con la misma probabilidad.
Cuando un sistema alcanza el equilibrio, la entropía es máxima. Esto significa que el número de microestados posibles para ese sistema también es máximo. Si quitamos una restricción al sistema (por ejemplo, le damos más volumen), el sistema evolucionará hacia un nuevo estado de equilibrio con una entropía aún mayor. Esto sucede porque ahora hay más microestados posibles para las partículas.
Por lo tanto, la entropía se puede identificar con el logaritmo del número de microestados posibles (Ω). La fórmula es:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): S = k_B \ln \Omega \, ,
donde kB es la constante de Boltzmann, que es solo un número para ajustar las unidades.
¿Se Puede Violar el Segundo Principio?
Hay algunas situaciones especiales en las que el segundo principio de la termodinámica no se aplica de la misma manera. Esto ocurre generalmente en sistemas muy pequeños, a escala atómica, o en periodos de tiempo extremadamente cortos (como femtosegundos o picosegundos).
El Teorema de Fluctuación de la Entropía
Este teorema, de la mecánica estadística, nos dice que, aunque la entropía de un sistema aislado tiende a aumentar, existe una pequeña probabilidad de que disminuya espontáneamente por un corto tiempo. Esto es más probable en sistemas muy pequeños.
El teorema de fluctuación fue propuesto en 1993 y ha sido probado en muchos sistemas. Establece que la probabilidad de que la entropía aumente es mucho mayor que la probabilidad de que disminuya. Sin embargo, para sistemas grandes (macroscópicos) y durante periodos de tiempo largos, la probabilidad de que la entropía disminuya es prácticamente cero. Por eso, el segundo principio de la termodinámica sigue siendo válido para el mundo que vemos a diario.
El Teorema de Recurrencia de Poincaré
El teorema de recurrencia de Poincaré dice que ciertos sistemas, después de un tiempo muy largo pero finito, volverán a un estado muy parecido al inicial. Esto significa que, por ejemplo, un gas que inicialmente está en una parte de un recipiente, tarde o temprano, debido a las colisiones de sus moléculas, podría volver a un estado similar, lo que implicaría una disminución temporal de la entropía.
Este teorema es similar al de fluctuación de la entropía, pero más sencillo de demostrar. Se aplica a sistemas mecánicos aislados con algunas limitaciones, como que todas las partículas deben estar en un volumen finito.
Véase también
 En inglés: Second law of thermodynamics Facts for Kids
En inglés: Second law of thermodynamics Facts for Kids
- Fluctuación cuántica
- Principios de la termodinámica
- Transmisión de calor
- Demonio de Maxwell
- Criterio de signos termodinámico
- Colectividad canónica