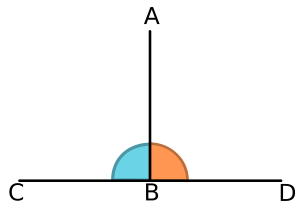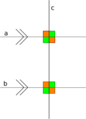Perpendicularidad para niños
En geometría, la perpendicularidad es una característica que tienen dos líneas o superficies cuando se cruzan formando un ángulo recto. Un ángulo recto mide exactamente 90 grados, como la esquina de un cuadrado. Esta idea es muy importante en el estudio de la geometría y la trigonometría, por ejemplo, en los triángulos rectángulos, que siempre tienen dos lados que son perpendiculares entre sí.
La perpendicularidad es una forma especial de una idea más general llamada ortogonalidad.
Contenido
¿Qué es la Perpendicularidad?
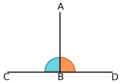
La perpendicularidad describe una relación especial entre dos elementos geométricos. Ocurre cuando se encuentran de tal manera que forman ángulos de 90 grados. Imagina las esquinas de una habitación o el cruce de dos calles que forman una "L" perfecta.
¿Entre qué elementos puede haber Perpendicularidad?
La relación de perpendicularidad puede darse entre diferentes tipos de elementos geométricos:
Perpendicularidad entre Rectas
- Rectas: Dos líneas que están en el mismo plano son perpendiculares si, al cruzarse, dividen ese plano en cuatro partes iguales. Cada una de estas partes es un ángulo recto. El punto donde se cruzan dos líneas perpendiculares se llama el "pie" de una línea sobre la otra.
- Semirrectas: Dos semirrectas (que son como "rayos" que salen de un punto y se extienden infinitamente en una dirección) son perpendiculares si forman ángulos rectos, sin importar si comparten el mismo punto de inicio o no.
Perpendicularidad entre Planos
- Planos: Dos planos (superficies planas e infinitas) son perpendiculares si, al cruzarse, forman cuatro ángulos diedros de 90 grados. Un ángulo diedro es como la "esquina" que se forma cuando dos planos se encuentran.
- Semiplanos: Dos semiplanos (que son la mitad de un plano, divididos por una línea) son perpendiculares si forman ángulos diedros de 90 grados. Generalmente, comparten la misma línea de origen.
Además, puede haber una relación de perpendicularidad entre una recta y un plano, o entre otros elementos combinados.
¿Cómo se construye una línea Perpendicular?
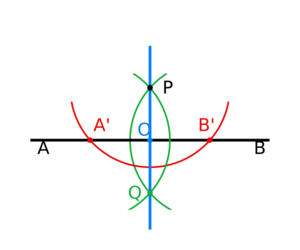
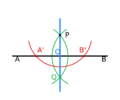
Puedes construir una línea perpendicular a otra usando solo una regla y compás. Aquí te explicamos cómo hacer una línea perpendicular a la línea AB que pase por un punto P:
- Paso 1 (rojo): Coloca la punta del compás en el punto P. Dibuja un círculo que corte la línea AB en dos puntos. Llama a estos puntos A' y B'. Estos puntos están a la misma distancia de P.
- Paso 2 (verde): Ahora, coloca la punta del compás en A' y dibuja un círculo que pase por P. Luego, coloca la punta del compás en B' y dibuja otro círculo que también pase por P. Estos dos nuevos círculos se cruzarán en dos puntos. Uno de ellos es P, y el otro lo llamaremos Q.
- Paso 3 (azul): Finalmente, une el punto P con el punto Q usando tu regla. La línea PQ que acabas de dibujar es perpendicular a la línea AB.
Esta construcción funciona porque los triángulos que se forman tienen lados y ángulos iguales, lo que garantiza que la línea PQ cruza AB formando un ángulo de 90 grados.
Propiedades de las líneas Perpendiculares
Las líneas perpendiculares tienen algunas propiedades interesantes:
- No es perpendicular a sí misma: Una línea no puede ser perpendicular a sí misma.
- Es simétrica: Si la línea A es perpendicular a la línea B, entonces la línea B también es perpendicular a la línea A. Es una relación mutua.
Perpendicularidad y Líneas Paralelas
Como puedes ver en la imagen, si dos líneas (como la línea a y la línea b) son perpendiculares a una tercera línea (la línea c), entonces todas las esquinas que se forman en la línea c son ángulos rectos. Esto significa que, en la Geometría euclidiana, cualquier par de líneas que son perpendiculares a una misma tercera línea, son paralelas entre sí. Esto se debe a una regla fundamental de la geometría.
Al revés, si una línea es perpendicular a una segunda línea, también será perpendicular a cualquier otra línea que sea paralela a esa segunda línea.
En la figura, todos los ángulos naranjas son iguales entre sí, y todos los ángulos verdes también son iguales entre sí. Esto ocurre porque los ángulos opuestos por el vértice son iguales, y los ángulos alternos internos que se forman cuando una línea cruza dos líneas paralelas también son iguales. Por lo tanto, si las líneas a y b son paralelas, cualquiera de estas afirmaciones es cierta si las demás también lo son:
- Uno de los ángulos del dibujo es un ángulo recto.
- Uno de los ángulos naranjas es igual a uno de los ángulos verdes.
- La línea c es perpendicular a la línea a.
- La línea c es perpendicular a la línea b.
Galería de imágenes
-
La semirrecta AB es perpendicular a la recta CD, porque los dos ángulos que conforma son de 90 grados (en naranja y azul, respectivamente).
-
Construcción de la perpendicular (azul) a la línea AB a través del punto P.
-
Las líneas a y b son paralelas, como se ve por los cuadrados, y están cortadas por la línea perpendicular c.
Véase también
En inglés: Right angle Facts for Kids
