Ley de los grandes números para niños
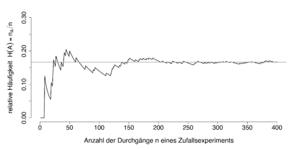
En la teoría de la probabilidad, la ley de los grandes números es un grupo de teoremas que explican cómo se comporta el promedio de una serie de eventos aleatorios cuando se repiten muchas veces.
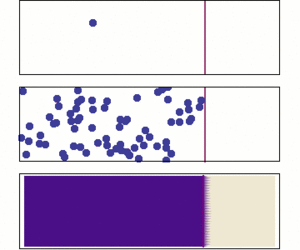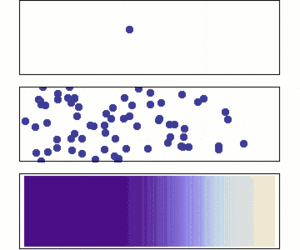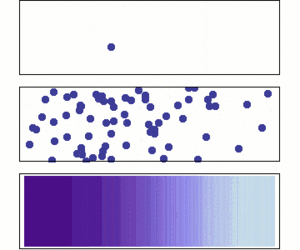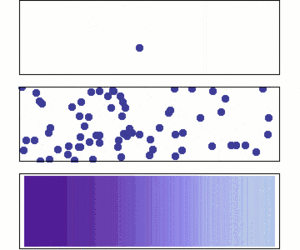
Estos teoremas nos dicen bajo qué condiciones el promedio de los resultados de muchos experimentos se acercará al valor esperado de esos eventos. El valor esperado es como el promedio que esperaríamos si el experimento se repitiera infinitas veces.
La ley de los grandes números nos ayuda a entender por qué el promedio de una muestra grande de algo (como las alturas de muchas personas) tiende a ser muy parecido al promedio de toda la población.
Cuando los eventos aleatorios tienen una variación limitada, el teorema central del límite nos ayuda a entender aún más cómo se comporta su promedio. Este teorema dice que, sin importar cómo se distribuyan los resultados individuales, la diferencia entre la suma de los resultados y su valor esperado se acerca a una distribución estándar.
A veces, la frase "ley de los grandes números" también se usa para explicar que la probabilidad de que un evento ocurra al menos una vez aumenta si se repite muchas veces. Por ejemplo, la probabilidad de que una persona gane la lotería es muy baja. Pero la probabilidad de que alguien gane la lotería es mucho más alta si muchas personas compran boletos.
Contenido
Historia de la Ley de los Grandes Números
El matemático italiano Gerolamo Cardano (1501–1576) fue uno de los primeros en decir, sin una prueba matemática, que las estadísticas que obtenemos de experimentos se vuelven más precisas cuantas más veces repetimos el experimento. Más tarde, esta idea se convirtió en la ley de los grandes números.
Una versión especial de esta ley fue demostrada por primera vez por Jacob Bernoulli. Le tomó más de 20 años desarrollar una prueba matemática muy precisa, que publicó en su libro Ars Conjectandi (El arte de la conjetura) en 1713. Bernoulli llamó a su descubrimiento su "Teorema Dorado".
En 1837, S.D. Poisson describió esta idea con más detalle y la llamó "la loi des grands nombres" (la ley de los grandes números). Desde entonces, se conoce con este nombre.
Después de Bernoulli y Poisson, otros matemáticos como Chebyshev, Markov, Borel, Cantelli, Kolmogorov y Khinchin también contribuyeron a mejorar y entender mejor esta ley. Gracias a ellos, ahora conocemos dos formas principales de la ley de los grandes números: la ley "débil" y la ley "fuerte".
Tipos de la Ley de los Grandes Números
Existen dos versiones principales de la ley de los grandes números, que describen cómo el promedio de muchos resultados se acerca al valor esperado.
Ley Débil
La ley débil de los grandes números dice que si tienes una serie muy larga de eventos aleatorios independientes que tienen el mismo valor esperado (promedio) y una variación limitada, entonces el promedio de esos eventos se acercará al valor esperado. Esto significa que la probabilidad de que el promedio de tus resultados esté muy cerca del valor esperado se vuelve casi 1 (o sea, casi seguro) a medida que haces más y más experimentos.
Ley Fuerte
La ley fuerte de los grandes números es una versión más estricta. Dice que si tienes una serie infinita de eventos aleatorios independientes e idénticamente distribuidos (es decir, que se comportan igual) y tienen un valor esperado finito, entonces el promedio de esos eventos no solo se acerca al valor esperado, sino que casi seguramente será igual a ese valor esperado a medida que el número de eventos se vuelve infinito.
Esta ley es la que justifica por qué podemos pensar en el valor esperado de un evento aleatorio como el "promedio a largo plazo" si repetimos el muestreo muchas veces.
Ejemplos de la Ley de los Grandes Números
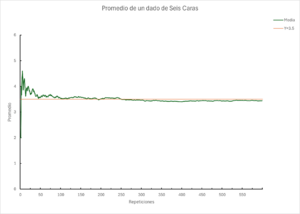
Imagina que lanzas un dado de seis caras. Cada cara (1, 2, 3, 4, 5 o 6) tiene la misma probabilidad de salir. El valor esperado del promedio de las tiradas es 3.5.
Según la ley de los grandes números, si lanzas el dado muchísimas veces, el promedio de todos los números que salgan se acercará a 3.5. Cuantas más veces lances el dado, más preciso será este promedio.
Otro ejemplo es lanzar una moneda "justa" (que tiene la misma probabilidad de caer cara o cruz). La probabilidad teórica de que salga cara es 1/2. Si lanzas la moneda un número "grande" de veces, la proporción de caras que obtengas "debería ser" aproximadamente 1/2. Es decir, la proporción de caras se acercará a 1/2 a medida que el número de lanzamientos sea muy grande.
Aunque la proporción de caras y cruces se acerca a la mitad, la diferencia en el número total de caras y cruces (por ejemplo, 500 caras y 490 cruces) puede aumentar a medida que lanzas más veces. Sin embargo, la relación entre esa diferencia y el número total de lanzamientos se acercará a cero. Esto significa que la diferencia esperada crece, pero más lentamente que el número de lanzamientos.
Un buen uso de la ley de los grandes números es el Método de Montecarlo. Estos métodos son programas de computadora que usan muestreos aleatorios repetidos para encontrar resultados numéricos. Cuantas más veces se repita el muestreo, mejor será la aproximación. Este método es muy útil cuando es difícil o imposible usar otras formas de cálculo.
Véase también
 En inglés: Law of large numbers Facts for Kids
En inglés: Law of large numbers Facts for Kids
- Teorema del límite central
- Teorema de Bernoulli
- Falacia del jugador
- Andréi Kolmogórov
- Andréi Márkov
- Aleksandr Jinchin
- Ley del logaritmo iterado
- Regresión a la media