Promedio para niños
Un promedio es un número que usamos para representar a un grupo de otros números. Imagina que tienes varias calificaciones en una materia; el promedio te da una idea general de cómo te fue. Hay diferentes tipos de promedios, y cada uno se usa en situaciones distintas.
El tipo de promedio más conocido es la media aritmética, que es lo que la mayoría de la gente piensa cuando dice "promedio". Para calcularla, sumas todos los números y luego divides el resultado entre la cantidad de números que sumaste.
En el mundo de la estadística, además de la media, existen otras formas de encontrar un valor central que represente a un grupo de datos, como la mediana y la moda. Estas se conocen como medidas de tendencia central.
Contenido
¿Cómo se calcula un promedio?
Existen varias maneras de calcular un promedio, dependiendo de lo que quieras representar. Aquí te explicamos las más comunes.
La Media Aritmética
La media aritmética es el promedio más común y fácil de entender. Para calcularla, sigue estos pasos:
- Suma todos los números de tu lista.
- Divide esa suma entre la cantidad total de números que hay en la lista.
Por ejemplo, si tienes las notas 7, 8 y 9 en tres exámenes, la media aritmética sería: (7 + 8 + 9) / 3 = 24 / 3 = 8. Así, tu promedio de notas es 8.
Si tienes solo dos números, como 2 y 8, la media aritmética es (2 + 8) / 2 = 5. Este número siempre estará entre el más pequeño (2) y el más grande (8).
La Media Geométrica
La media geométrica se usa a menudo cuando los números representan tasas de crecimiento o cambios porcentuales. Para calcularla con números positivos:
- Multiplica todos los números de tu lista.
- Calcula la raíz enésima de ese producto, donde "n" es la cantidad de números en tu lista.
Por ejemplo, la media geométrica de 2 y 8 es la raíz cuadrada de (2 * 8) = la raíz cuadrada de 16 = 4.
La Media Armónica
La media armónica es útil para calcular promedios de tasas o velocidades, especialmente cuando se recorren distancias iguales. Para calcularla:
- Toma el recíproco de cada número (1 dividido por el número).
- Calcula la media aritmética de esos recíprocos.
- Finalmente, toma el recíproco de ese resultado.
Por ejemplo, si viajas de un punto A a un punto B a 60 km/h y regresas de B a A a 40 km/h, la velocidad promedio no es 50 km/h. La media armónica sería: 2 / ((1/60) + (1/40)) = 2 / ( (2+3)/120 ) = 2 / (5/120) = 2 * (120/5) = 2 * 24 = 48 km/h.
Relación entre las Medias
Para cualquier grupo de números positivos, siempre se cumple una relación interesante: La Media Aritmética (AM) es mayor o igual que la Media Geométrica (GM), y la Media Geométrica (GM) es mayor o igual que la Media Armónica (HM). Es decir: AM ≥ GM ≥ HM.
Otras Medidas de Tendencia Central
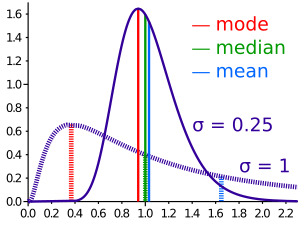
Además de la media aritmética, la mediana y la moda son otras formas de encontrar el "centro" de un grupo de datos.
| Tipo | Descripción | Ejemplo | Resultado |
|---|---|---|---|
| Media aritmética | Suma de valores de un conjunto de datos dividido por el número de valores. | (1 + 2 + 2 + 3 + 4 + 7 + 9) / 7 | 4 |
| Mediana | Valor central que divide el conjunto de datos en dos mitades iguales. | 1, 2, 2, 3, 4, 7, 9 | 3 |
| Moda | Valor que aparece con mayor frecuencia en un conjunto de datos. | 1, 2, 2, 3, 4, 7, 9 | 2 |
| Rango medio | La media aritmética del valor más alto y el más bajo de un conjunto. | (1 + 9) / 2 | 5 |
La Moda
La moda es el número que más se repite en una lista. Por ejemplo, en la lista (1, 2, 2, 3, 3, 3, 4), el número 3 es la moda porque aparece tres veces, más que cualquier otro número.
A veces, puede haber dos o más números que se repitan con la misma frecuencia y sean los que más aparecen. En esos casos, algunos dicen que todos esos números son la moda, mientras que otros dicen que no hay una moda única.
La Mediana
La mediana es el número que se encuentra justo en el medio de un grupo de datos cuando los ordenas de menor a mayor.
Para encontrar la mediana:
- Primero, ordena todos los números de tu lista de menor a mayor.
- Luego, ve eliminando un número de cada extremo (el más pequeño y el más grande) hasta que te quede solo uno o dos números en el centro.
- Si queda un solo número, esa es la mediana.
- Si quedan dos números, la mediana es la media aritmética de esos dos números (los sumas y los divides entre 2).
Por ejemplo, para la lista 1, 7, 3, 13: 1. Ordena: 1, 3, 7, 13. 2. Elimina el 1 y el 13. Te queda: 3, 7. 3. Como quedan dos números, la mediana es (3 + 7) / 2 = 5.
El Rango Medio
El rango medio es el promedio del valor más alto y el valor más bajo de un conjunto de datos. Se calcula sumando el número más grande y el más pequeño, y luego dividiendo entre 2.
Tipos de promedios en resumen
| Nombre | Descripción |
|---|---|
| Media aritmética | La suma de todos los valores dividida por la cantidad de valores. |
| Mediana | El valor central que divide el conjunto de datos en dos mitades. |
| Moda | El valor que aparece con mayor frecuencia en el conjunto de datos. |
| Media geométrica | La raíz enésima del producto de todos los valores. |
| Media armónica | El recíproco de la media aritmética de los recíprocos de los valores. |
| Media cuadrática (o RMS) | La raíz cuadrada de la media de los cuadrados de los valores. |
| Media ponderada | Una media donde algunos valores tienen más "peso" o importancia que otros. |
| Media truncada | La media aritmética después de quitar un cierto número de valores extremos (los más altos y los más bajos). |
| Rango medio | La media aritmética del valor más alto y el más bajo. |
Promedios en el tiempo
Media móvil
Imagina que tienes datos que cambian con el tiempo, como las temperaturas diarias o los precios de algo en el mercado. A veces, estos datos pueden tener muchos altibajos, y es difícil ver una tendencia clara. Para suavizar estos datos y ver mejor los patrones, se usa la media móvil.
Funciona así: eliges un número (por ejemplo, 7 para una semana). Luego, calculas la media aritmética de los primeros 7 valores. Después, te mueves un día, quitas el valor más antiguo y añades el valor más nuevo, y vuelves a calcular la media de esos 7 valores. Así, obtienes una nueva serie de datos más suave que te ayuda a ver las tendencias a largo plazo.
Historia de los promedios
Origen del concepto
La idea de usar la media aritmética para estimar un valor real a partir de varias mediciones comenzó a ser común en el XVI. En ese tiempo, los astrónomos la usaban para reducir los errores al medir cosas como la posición de los planetas o el tamaño de la luna. Pensaban que si sumaban muchos errores pequeños, estos se anularían entre sí, dando un resultado más preciso.
Antes de eso, ya había ideas similares. Por ejemplo, en la astronomía árabe de los siglos IX al XI, se usaba el "rango medio" (el promedio de los dos valores extremos).
Incluso hay registros más antiguos que sugieren el uso de promedios. Alrededor del año 700 a.C., los comerciantes y marineros acordaban que si la carga de un barco se dañaba en el mar, las pérdidas debían compartirse por igual entre todos. Esto podría haberse calculado usando algún tipo de promedio, aunque no hay registros directos de cómo lo hacían.
El origen de la palabra "promedio"
La palabra "promedio" (average en inglés) tiene una historia interesante que viene del comercio marítimo medieval en el Mediterráneo. La raíz de la palabra se encuentra en el árabe "awar", que significaba un defecto o algo dañado, especialmente mercancías.
En latín, en los siglos XII y XIII, "avaria" significaba "daños, pérdidas y gastos no normales de un viaje en barco". Este significado se extendió a otros idiomas como el francés y el inglés.
La gran transformación del significado en inglés ocurrió en los contratos de leyes marítimas. Si un barco en una tormenta tenía que tirar parte de su carga al mar para salvarse, todos los comerciantes con bienes en el barco compartían las pérdidas de forma proporcional. De ahí, la palabra "average" empezó a usarse para hablar de pérdidas repartidas de manera equitativa. A mediados del XVIII, el significado actual de "promedio" como la media aritmética se estableció en inglés.
Galería de imágenes
Véase también
 En inglés: Average Facts for Kids
En inglés: Average Facts for Kids