Autómata finito para niños
Un autómata finito (también conocido como máquina de estado finito) es como un pequeño robot o una máquina imaginaria que sigue reglas muy específicas para procesar información. Piensa en él como un sistema que puede estar en diferentes "estados" (como si tuviera diferentes modos de funcionamiento) y que cambia de un estado a otro según lo que recibe como entrada.
Este modelo está formado por:
- Un alfabeto: Es el conjunto de símbolos que la máquina puede leer (por ejemplo, letras, números, o 0 y 1).
- Un conjunto de estados: Son los diferentes modos en los que la máquina puede estar. Siempre hay un número limitado de estos estados.
- Una función de transición: Son las reglas que le dicen a la máquina a qué estado debe ir desde el estado actual, dependiendo del símbolo que lea.
- Un estado inicial: Es el estado donde la máquina siempre empieza.
- Un conjunto de estados finales (o de aceptación): Son los estados donde la máquina puede terminar su trabajo y decir que ha "aceptado" la entrada.
La máquina comienza en su estado inicial. Luego, lee una secuencia de símbolos (la "entrada") uno por uno. A medida que lee cada símbolo, usa la función de transición para decidir a qué nuevo estado moverse. Al final, si la máquina termina en uno de los estados finales, significa que la secuencia de símbolos que leyó es "válida" o "aceptada" por ella.
Los autómatas finitos se usan para reconocer patrones en secuencias de símbolos, como las que forman los "lenguajes regulares". Estos son los tipos de lenguajes más sencillos que se pueden describir con reglas.
Contenido
Historia de los autómatas finitos
Los autómatas finitos tienen una historia interesante que se mezcla con el desarrollo de las computadoras y la lógica.
Primeros pasos y conceptos clave
Se cree que la idea de los autómatas finitos ya estaba presente de forma indirecta en máquinas electromecánicas a principios del siglo XX. En 1907, un matemático ruso llamado Andréi Márkov desarrolló un concepto llamado "cadena de Márkov". En estas cadenas, la probabilidad de que ocurra un evento depende del evento anterior. Esta idea de "recordar" el paso anterior es similar a cómo funcionan los autómatas finitos, donde el estado actual depende del estado anterior y del símbolo leído.
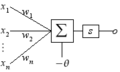
Más tarde, en 1943, surgió una idea más formal de los autómatas finitos con el modelo de Neurona de McCulloch-Pitts. Este modelo, que se inspira en cómo funcionan las neuronas, también usa diagramas con estados y transiciones, y los conceptos de entrada y salida.
Crecimiento y aplicaciones prácticas
Durante la década de 1950, el estudio de estas máquinas se hizo muy popular. A menudo se les llamaba "máquinas de secuencia". En esta época se descubrieron muchas de sus propiedades básicas, como su relación con los lenguajes regulares y su equivalencia con las expresiones regulares. Hacia el final de esta década, en 1959, los informáticos Michael O. Rabin y Dana Scott introdujeron el concepto de autómata finito no determinista, que veremos más adelante.
En la década de 1960, se encontró una conexión entre los autómatas finitos y otros sistemas. Pero fue en la década de 1970, con el desarrollo del sistema operativo Unix, cuando los autómatas finitos encontraron un uso masivo y práctico. Se usaron para diseñar "analizadores léxicos" (programas que leen código y lo dividen en partes más pequeñas) y para buscar y reemplazar texto en documentos. Desde entonces, también se han usado en sistemas dinámicos, que son sistemas que cambian con el tiempo.
¿Cómo se define un autómata finito?
Para entender mejor un autómata finito, podemos describirlo con cinco elementos clave:
- Q: Es el grupo de todos los estados posibles en los que puede estar la máquina.
- Σ: Es el alfabeto, es decir, todos los símbolos que la máquina puede leer.
- q0: Es el estado inicial, el punto de partida de la máquina.
- δ: Es la función de transición, que nos dice a qué estado se mueve la máquina desde un estado actual al leer un símbolo.
- F: Es el grupo de estados finales o de "aceptación". Si la máquina termina en uno de estos estados, la entrada es válida.
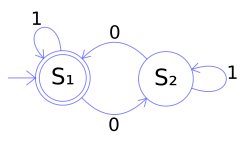
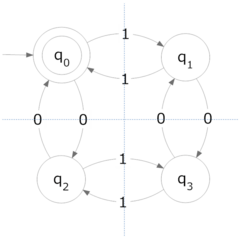
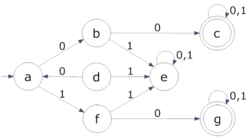
Representación con diagramas de estados
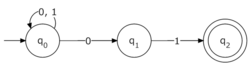
Una forma muy útil de visualizar los autómatas finitos es usando diagramas, que son como mapas de sus estados y transiciones:
- Los estados se dibujan como círculos, y dentro de cada círculo se escribe el nombre del estado.
- Las transiciones (los cambios de un estado a otro) se muestran con flechas que van de un círculo a otro. Sobre cada flecha se escribe el símbolo que la máquina debe leer para hacer esa transición.
- El estado inicial se indica con una flecha que llega a él "de la nada".
- Los estados finales se dibujan con un doble círculo.
Representación con tablas de transiciones
Otra forma de describir un autómata finito es usando una tabla. Esta tabla muestra de manera organizada cómo la máquina cambia de estado.
|
|
La primera tabla muestra cada regla de transición por separado. La segunda es más compacta y usa una flecha para el estado inicial y un asterisco para los estados finales.
¿Cómo funciona un autómata finito?
Cuando un autómata finito empieza a procesar una secuencia de símbolos, siempre se encuentra en su estado inicial. A medida que lee cada símbolo de la secuencia, la máquina usa su función de transición para decidir a qué nuevo estado debe moverse.
Cuando ha leído el último símbolo de la secuencia, la máquina se detiene en un estado final. Si ese estado final es uno de los "estados de aceptación" (los que tienen doble círculo en el diagrama), entonces la secuencia de símbolos es reconocida por el autómata. Si no termina en un estado de aceptación, la secuencia no es reconocida.
Es importante recordar que un autómata finito siempre tiene un único estado inicial. Sin embargo, puede tener uno o varios estados finales. Incluso, el estado inicial puede ser también un estado final.
Tipos de autómatas finitos
Existen dos tipos principales de autómatas finitos: los deterministas y los no deterministas.
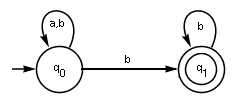
Autómata finito determinista (AFD)
Un autómata finito determinista (AFD) es un tipo de autómata finito donde las reglas son muy claras: para cada estado en el que se encuentre la máquina y para cada símbolo que lea, siempre hay una única transición posible a un siguiente estado.
En un AFD, no pueden ocurrir estas situaciones:
- Que desde un mismo estado, al leer el mismo símbolo, la máquina pueda ir a dos estados diferentes.
- Que la máquina pueda cambiar de estado sin leer ningún símbolo (a menos que sea un estado final sin más transiciones).
Autómata finito no determinista (AFND)
Un autómata finito no determinista (AFND) es diferente de un AFD. En un AFND, puede haber al menos un estado donde, al leer un símbolo, la máquina tiene varias opciones de a qué estado moverse.
En un AFND, pueden ocurrir estas situaciones:
- Que desde un mismo estado, al leer el mismo símbolo, la máquina pueda ir a dos o más estados diferentes.
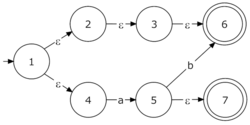
- Que la máquina pueda cambiar de estado sin leer ningún símbolo. A esto se le llama "transición vacía" o "transición ε". Si un AFND tiene estas transiciones, se le llama autómata finito no determinista con transiciones vacías (AFND-ε).
Cuando un AFND tiene varias opciones, podemos imaginar que la máquina "prueba" todos los caminos posibles al mismo tiempo, o que "adivina" cuál es el camino correcto. Los AFD son un caso especial de los AFND, donde simplemente no hay opciones múltiples.
Equivalencias entre autómatas finitos
Se dice que dos autómatas finitos son equivalentes si ambos reconocen exactamente el mismo conjunto de secuencias de símbolos.
Es interesante saber que cualquier patrón que pueda ser descrito por una expresión regular (que es una forma de escribir lenguajes regulares) puede ser reconocido por un autómata finito determinista, y viceversa.
El proceso para pasar de una expresión regular a un AFD suele ser así: 1. Primero, se construye un AFND-ε, que es el más fácil de crear porque tiene menos restricciones. 2. Luego, ese AFND-ε se transforma en un AFND equivalente, eliminando las transiciones vacías. 3. Finalmente, ese AFND se convierte en un AFD equivalente.
Esto significa que, aunque los AFND y AFND-ε parecen más complejos por sus múltiples opciones, siempre se puede encontrar un AFD que haga exactamente el mismo trabajo.
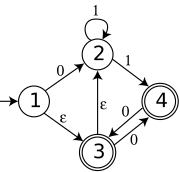
Conversión de un AFND-ε a un AFND
Para convertir un AFND-ε a un AFND, se usa un concepto llamado "clausura-ε". La clausura-ε de un estado es el conjunto de todos los estados a los que se puede llegar desde ese estado usando solo transiciones vacías.
El proceso es el siguiente: 1. Calcula la clausura-ε del estado inicial. Este será el estado inicial del nuevo AFND. 2. Para cada símbolo del alfabeto, mira a qué estados puedes llegar desde los estados de tu nuevo conjunto, y luego calcula la clausura-ε de esos nuevos estados. Si encuentras nuevos conjuntos de estados, estos serán los nuevos estados de tu AFND. 3. Repite el paso 2 hasta que no puedas encontrar más estados nuevos.
En el ejemplo de la imagen, el AFND-ε inicial se convierte en un AFD (que es un tipo de AFND) al eliminar las transiciones vacías.
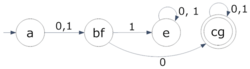
Conversión de un AFND a un AFD
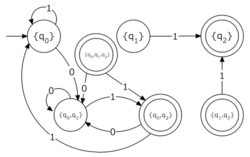
Cualquier AFND puede transformarse en un AFD equivalente. El proceso implica crear nuevos estados en el AFD que representen combinaciones de estados del AFND original.
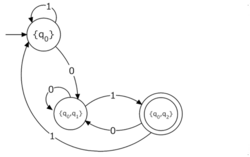
Los pasos son: 1. Los nuevos estados del AFD serán todos los posibles grupos de estados del AFND original. Los nuevos estados finales serán aquellos grupos que contengan al menos un estado final del AFND original. 2. Las nuevas transiciones se definen observando a qué estados se podía llegar en el AFND desde un grupo de estados, al leer un símbolo. 3. Finalmente, se eliminan los estados y transiciones que no se pueden alcanzar desde el estado inicial del nuevo AFD. Esto simplifica el autómata.
En las figuras del ejemplo, un AFND con tres estados se convierte en un AFD. Los estados del AFD son combinaciones de los estados del AFND. Al final, se eliminan los estados que no son accesibles desde el estado inicial, obteniendo un AFD más simple.
Minimización de un AFD
Minimizar un AFD significa encontrar el AFD más pequeño posible que reconozca el mismo lenguaje. Esto se hace combinando estados que son "equivalentes", es decir, que se comportan de la misma manera.
Un algoritmo para minimizar un AFD es: 1. Elimina cualquier estado al que no se pueda llegar desde el estado inicial. 2. Crea una tabla con todos los pares de estados restantes. 3. Marca en la tabla los pares donde un estado es final y el otro no lo es, ya que estos estados no pueden ser equivalentes. 4. Para cada par de estados sin marcar y para cada símbolo, observa a qué estados se mueven. Si esos nuevos estados ya están marcados como distinguibles, entonces el par original también es distinguible y se marca. Si no, se anota que dependen de ese par. 5. Agrupa los estados que no quedaron marcados. Estos son los estados equivalentes que se pueden unir.
Después de este proceso, obtendrás un AFD con el menor número de estados posible, pero que sigue reconociendo el mismo lenguaje.
Generalizaciones de autómatas finitos
Los autómatas finitos son la base de modelos más complejos que pueden hacer más cosas.
- Transductores de estados finitos: Son como autómatas finitos que no solo reconocen una entrada, sino que también producen una salida. Tienen un alfabeto de salida diferente al de entrada. Las máquinas de Moore y Mealy son ejemplos de estos transductores y se usan para modelar sistemas que cambian su salida según su estado y entrada.
- Autómatas con pila: Estos son más poderosos. Además de los estados y transiciones, tienen una "pila" (una especie de memoria temporal donde pueden guardar y sacar información). Esto les permite reconocer lenguajes más complejos que los lenguajes regulares.
Véase también
 En inglés: Automaton Facts for Kids
En inglés: Automaton Facts for Kids
- Lenguaje regular
- Teoría de autómatas
- Sistema combinacional
- Autómata con pila
- Máquina de Turing
- Máquina abstracta
Galería de imágenes