robot de la enciclopedia para niños

Notación matemática para niños

Enciclopedia para niños

La notación matemática es como un lenguaje especial que usan los matemáticos para escribir ideas, relaciones y operaciones de forma clara y precisa. Imagina que es un código secreto que todos los que estudian matemáticas pueden entender. En lugar de usar muchas palabras, se usan símbolos que representan conceptos, relaciones o fórmulas. Estos símbolos no son solo abreviaturas, ¡tienen su propio significado!

Algunas reglas básicas para escribir esta notación son:

  • Los símbolos que son una sola letra, como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \scriptstyle a, \, b, \, x, \,y , se escriben en letra cursiva.
  • Los símbolos que tienen varias letras, como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \scriptstyle \cos \alpha (que significa coseno de alfa) o Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \scriptstyle \exp x (que significa exponencial de x), se escriben en letra normal (redonda). Por ejemplo, para el logaritmo neperiano de x, se escribe Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \scriptstyle \ln x , no Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \scriptstyle lnx , porque esto último podría confundirse con la multiplicación de l, n y x.
  • Según una norma internacional llamada ISO/IEC 80000, algunas constantes matemáticas importantes (como 'e' e 'i') y operadores especiales también se escriben con letra normal.

¿Qué es la Teoría de Conjuntos?

La teoría de conjuntos es una parte de las matemáticas que estudia las colecciones de objetos. A estas colecciones las llamamos conjuntos. Los objetos dentro de un conjunto se llaman elementos.

Símbolos para Conjuntos

Aquí te mostramos algunos símbolos que se usan para hablar de conjuntos:

Relación Notación Se lee
Pertenencia 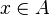x\in A x pertenece a A (x es un elemento del conjunto A)
Inclusión 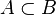A\subset B A está contenido en B (todos los elementos de A también están en B, pero A no es igual a B)
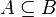A\subseteq B A está contenido en B o es igual que B
Inclusión 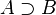A\supset B A contiene a B (todos los elementos de B también están en A, pero B no es igual a A)
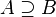A\supseteq B A contiene a B o es igual que B

Si ves una barra cruzada sobre un símbolo, significa lo contrario. Por ejemplo, 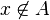x\not\in A se lee "x no pertenece a A".

Conjuntos de Números Importantes

En matemáticas, usamos símbolos especiales para representar grupos de números que usamos mucho. Estos símbolos suelen ser letras dobles o "blackboard bold":

Símbolo Significado en matemáticas
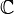\mathbb C \! Números complejos (números que incluyen una parte "imaginaria")
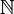\mathbb N\! Números naturales (los números que usamos para contar: 1, 2, 3, ...)
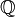\mathbb Q\! Números racionales (números que se pueden escribir como una fracción, como 1/2 o 3/4)
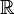\mathbb R\! Números reales (todos los números que puedes imaginar en una línea numérica, incluyendo decimales y fracciones)
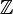\mathbb Z\! Números enteros (números completos, positivos, negativos y el cero: ..., -2, -1, 0, 1, 2, ...)

Ejemplos de Conjuntos Numéricos

  • Los números naturales (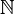\mathbb{N}) son: {1, 2, 3, ...}
  • Si incluimos el cero, se escribe 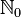\mathbb{N}_0 o Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbb{N}^{*} : {0, 1, 2, 3, ...}
  • Los números enteros (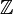\mathbb{Z}) son: {..., -3, -2, -1, 0, 1, 2, 3, ...}
  • Los números racionales (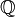\mathbb{Q}) son todas las fracciones 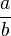\frac{a}{b} donde 'a' y 'b' son números enteros y 'b' no es cero.
  • Los números reales (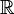\mathbb{R}) incluyen todos los números que no son imaginarios. Los números irracionales son los números reales que no se pueden escribir como fracción (como pi o la raíz cuadrada de 2).
  • Los números complejos (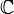\mathbb{C}) son números que tienen una parte real y una parte imaginaria.

Expresiones y Relaciones

La notación matemática también nos ayuda a mostrar cómo se relacionan los números o las cantidades.

Símbolos de Comparación

Relación Notación Se lee
Igualdad x = y x es igual que y
Menor que x < y x es menor que y
Mayor que x > y x es mayor que y
Aproximado 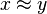x \approx y x es aproximadamente igual que y

Cuantificadores: ¿Cuántos hay?

Los cuantificadores nos dicen "cuántos" elementos cumplen una condición.

Cuantificador Notación Se lee
Cuantificador universal 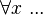\forall x\ ... Para todo x... (significa que la condición se cumple para cada x)
Cuantificador existencial 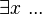\exists x\ ... Existe por lo menos un x... (significa que hay al menos un x que cumple la condición)
Cuantificador existencial con unicidad 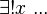\exists! x\ ... Existe un único x... (significa que solo hay un x que cumple la condición)
Tal que 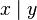x \mid y x, tal que y (se usa para especificar una condición)
Por lo tanto 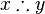x \therefore y x, por lo tanto y (se usa para indicar una conclusión)

Por ejemplo, el Teorema de Weierstrass dice que si tienes una función continua en un intervalo cerrado, esa función siempre tendrá un valor máximo y un valor mínimo en ese intervalo. En notación matemática, esto se puede escribir de forma muy compacta.

Lógica y Operadores

La lógica matemática usa símbolos para representar ideas como "y", "o" y "no". Esto es muy útil en la programación de computadoras y en la toma de decisiones.

Operadores Lógicos Básicos

Los operadores lógicos más comunes son la conjunción (y), la disyunción (o) y la negación (no). Si 'p' y 'q' son dos afirmaciones (proposiciones):

Operación Notación Se lee
Negación 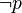\neg p no 'p' (significa lo contrario de 'p')
Conjunción 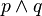p \land q 'p' y 'q' (es verdad solo si 'p' es verdad Y 'q' es verdad)
Disyunción 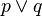p \lor q 'p' o 'q' (es verdad si 'p' es verdad O 'q' es verdad, o ambas)

Estos operadores nos ayudan a construir "declaraciones atómicas" que nos dicen cuándo una combinación de afirmaciones es verdadera.

Implicación: Si... Entonces...

Una combinación muy útil es la implicación. Se escribe 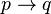p \to q o p \Rightarrow q y se lee "si 'p' entonces 'q'". Esto significa que si 'p' es verdad, entonces 'q' también debe ser verdad. Pero 'q' podría ser verdad por otras razones, incluso si 'p' no lo es.

Si p \Rightarrow q (si p, entonces q) y q \Rightarrow p (si q, entonces p), entonces se escribe p \Leftrightarrow q. Esto se lee "'p' si y solo si 'q'". Significa que 'p' y 'q' siempre son verdaderas o falsas al mismo tiempo.

Estos operadores lógicos se usan mucho en la programación de computadoras y en la vida diaria para tomar decisiones. Por ejemplo:

  • Si salgo tarde de mi casa y no tengo vehículo, entonces llegaré tarde al trabajo.
  • Si el libro está deteriorado o no lo uso, entonces lo donaré.

Cuantificadores en Lógica

Los cuantificadores que vimos antes también se usan en lógica para decir cuándo una afirmación es verdadera.

  • Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \forall x\ ,\ p se lee "para todo x, es verdad que p".
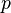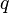  • Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \exists y \mid q se lee "existe por lo menos un y tal que q es verdad".

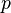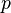Estos dos cuantificadores están relacionados. Por ejemplo, decir "no es para todo x que p es verdad" es lo mismo que decir "existe un x tal que p es falsa".

Galería de imágenes

Véase también

Kids robot.svg En inglés: Mathematical notation Facts for Kids

  • Anexo:Tabla de símbolos matemáticos
  • Anexo:Constantes matemáticas
Obtenido de «https://ninos.kiddle.co/index.php?title=Notación_matemática&oldid=5040087»
kids search engine
Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:
Notación matemática para Niños. Enciclopedia Kiddle.