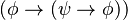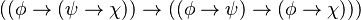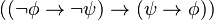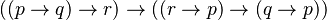Jan Łukasiewicz para niños
Jan Łukasiewicz (nacido el 21 de diciembre de 1878 y fallecido el 13 de febrero de 1956) fue un importante matemático, lógico y filósofo de Polonia. Nació en Leópolis, una ciudad que hoy forma parte de Ucrania.
Su trabajo principal se centró en la lógica, que es el estudio de cómo razonamos y pensamos de forma correcta. Łukasiewicz buscó nuevas formas de entender la lógica tradicional, especialmente en conceptos como el principio de no contradicción (que dice que algo no puede ser y no ser al mismo tiempo) y el principio del tercero excluido (que afirma que algo es verdadero o falso, sin una tercera opción).
También desarrolló la lógica plurivalente, que es un tipo de lógica donde las afirmaciones pueden tener más de dos valores de verdad (no solo verdadero o falso). Él creó una lógica con tres valores, lo que fue una idea muy novedosa. Además, se interesó por cómo las personas crean teorías científicas, con ideas parecidas a las de otro pensador llamado Karl Popper.
Entre sus libros más conocidos se encuentran Elementos de lógica matemática y La silogística de Aristóteles desde el punto de vista de la lógica formal moderna.
Contenido
¿Quién fue Jan Łukasiewicz?
Sus primeros años y educación
Jan Łukasiewicz nació en 1878. Desde 1890 hasta 1902, estudió con un profesor llamado Kazimierz Twardowski en Leópolis. En 1902, obtuvo su doctorado en matemáticas y filosofía de la Universidad de Leópolis con las más altas calificaciones. Se convirtió en profesor en 1906.
Su carrera y aportes importantes
En 1910, escribió ensayos sobre los principios de no contradicción y del tercero excluido. En 1911, fue nombrado profesor extraordinario en Leópolis. En 1915, fue invitado a la nueva Universidad de Varsovia.
Un año después, en 1916, se declaró el nuevo Reino de Polonia. En 1917, Łukasiewicz desarrolló su cálculo proposicional trivalente, que es una forma de lógica con tres valores de verdad, y también criticó el principio del tercero excluido.
En 1919, ocupó un cargo importante como Ministro Polaco de Educación. Entre 1920 y 1939, fue profesor en la Universidad de Varsovia. Allí, junto con Stanislaw Leśniewski, fundó la famosa escuela de lógica de Leópolis-Varsovia. Otros grandes pensadores como Alfred Tarski, Stefan Banach, Hugo Steinhaus, Zygmunt Janiszewski y Stefan Mazurkiewicz también formaron parte de esta escuela.
En 1928, se casó con Regina Barwinska.
Últimos años y legado
Después de la Segunda Guerra Mundial, en 1946, Łukasiewicz se exilió en Bélgica. Ese mismo año, le ofrecieron una cátedra en el University College Dublin en Irlanda. En 1953, escribió su autobiografía. Finalmente, Jan Łukasiewicz falleció en Dublín en 1956.
¿Qué es la axiomatización de la lógica proposicional?
Uno de los trabajos más conocidos de Łukasiewicz fue su forma de organizar la lógica proposicional usando axiomas. Los axiomas son como reglas básicas que se aceptan como verdaderas sin necesidad de demostración.
Los axiomas de Łukasiewicz
Una de sus formas de organizar la lógica proposicional usa solo tres axiomas. En la forma moderna, se pueden escribir así:
A partir de estas tres reglas básicas, se pueden deducir todas las afirmaciones válidas de la lógica proposicional usando solo dos métodos: la sustitución (cambiar una parte de la fórmula por otra) y el modus ponens (una regla de inferencia que permite sacar una conclusión si se cumplen ciertas condiciones).
Łukasiewicz también revisó un sistema axiomático anterior de Nicod, que usaba solo un tipo de conexión lógica y un solo axioma:
La notación polaca
Otro gran logro de Łukasiewicz fue crear una forma de escribir la lógica proposicional que no dejaba lugar a dudas. Esta forma de escribir se conoce como notación polaca. Con ella, no se necesitan paréntesis ni otros signos para saber el orden en que se aplican las operaciones lógicas. En la notación polaca, los símbolos de las operaciones lógicas se ponen antes de los elementos a los que afectan, en lugar de entre ellos. Esta notación es muy importante en las ciencias de la computación.
Véase también
 En inglés: Jan Łukasiewicz Facts for Kids
En inglés: Jan Łukasiewicz Facts for Kids
- Notación polaca
- Alfred Tarski
- Escuela de Leópolis-Varsovia
Galería de imágenes