Notación polaca para niños
La notación polaca, también conocida como notación de prefijo, es una forma especial de escribir operaciones en lógica, aritmética, álgebra y computación. Lo más importante de esta notación es que los operadores (como +, -, * o /) se colocan antes de los números o valores sobre los que actúan.
Esta notación fue inventada alrededor de 1920 por el lógico polaco Jan Łukasiewicz. Su objetivo era hacer más sencilla la lógica proposicional, eliminando la necesidad de usar paréntesis u otros signos de agrupación. Si cada operador siempre necesita el mismo número de valores (por ejemplo, la suma siempre necesita dos números), la notación polaca permite entender las operaciones sin confusiones.
Aunque ya no se usa mucho en lógica, la notación polaca es muy importante en las ciencias de la computación.
Contenido
¿Cómo funciona la notación polaca en aritmética?
En la notación polaca, el operador va primero. Por ejemplo, para sumar uno y dos, en lugar de escribir "1 + 2", se escribe "+ 1 2".
Ejemplos de operaciones aritméticas
Cuando las operaciones son más complicadas, el operador sigue yendo antes que sus valores. Estos valores pueden ser a su vez otras operaciones.
Por ejemplo, la expresión que normalmente escribiríamos como:
- (5 - 6) * 7
En notación polaca se escribiría así:
- * (- 5 6) 7
O de forma más sencilla, sin paréntesis:
- * - 5 6 7
Como los operadores aritméticos básicos (suma, resta, multiplicación, división) siempre trabajan con dos números, la notación polaca no necesita paréntesis para saber qué operación va primero.
Comparación con la notación normal
En la notación que usamos normalmente (llamada notación de infijo), los paréntesis son muy importantes. Si los movemos o los quitamos, el significado de la operación puede cambiar.
Por ejemplo, si cambiamos la expresión:
- 5 - (6 * 7)
O si quitamos los paréntesis:
- 5 - 6 * 7
El resultado sería diferente. Sin embargo, en notación polaca, la expresión para "5 - (6 * 7)" se escribiría así:
- - 5 * 6 7
Aquí, la resta se hace después de que se haya calculado la multiplicación de 6 y 7. En la notación polaca, el orden de las operaciones se entiende por la posición de los operadores, no por los paréntesis.
La notación polaca para operaciones aritméticas sencillas es interesante para aprender. Se ha usado en algunas calculadoras, como las de la marca HP. También es un concepto clave para entender cómo funcionan los programas que traducen código (llamados compiladores).
Notación polaca en la programación de computadoras
La notación de prefijo se usa mucho en lenguajes de programación como Lisp. En Lisp, se usan paréntesis, pero es porque los operadores pueden trabajar con diferentes cantidades de valores. Otros lenguajes de programación, como PostScript, usan una notación similar llamada notación polaca inversa, donde el operador va después de los valores.
Es importante recordar que en una expresión con operadores que trabajan con dos valores, siempre debe haber un número de valores que sea uno más que el número de operadores. Si no, la expresión no tendría sentido.
¿Cómo se determina el orden de las operaciones?
El orden en que se realizan las operaciones en la notación polaca es muy claro. Una regla importante es que la operación se aplica al primer valor por el segundo valor. Esto es clave para operaciones como la división o la resta, donde el orden importa.
Por ejemplo, la expresión:
- / 10 5
Significa "Divide 10 entre 5", lo que da como resultado 2. No es lo mismo que dividir 5 entre 10.
Ventajas de la notación polaca
La notación polaca es muy útil en sistemas que usan una "pila" (como una pila de platos, donde solo puedes añadir o quitar el de arriba). Permite saber el orden de las operaciones sin necesidad de paréntesis. No tienes que memorizar reglas de prioridad (como "primero multiplicaciones y divisiones, luego sumas y restas").
Para resolver una expresión en notación polaca, se lee de izquierda a derecha. Cuando encuentras un operador, buscas los dos valores que le siguen. Si encuentras otro operador antes de los dos valores, dejas el primer operador a un lado y resuelves el nuevo operador primero. Este proceso se repite hasta que se resuelve una operación. Cuando una operación se resuelve, el operador y sus dos valores se reemplazan por un solo resultado, y el proceso continúa hasta que toda la expresión se reduce a un único resultado final.
Aquí tienes un ejemplo de cómo se resuelve una expresión compleja en notación polaca:
La expresión normal `((15 / (7 - (1 + 1))) * 3) - (2 + (1 + 1))` se resuelve así en notación polaca:
- * / 15 - 7 + 1 1 3 + 2 + 1 1 = - * / 15 - 7 2 3 + 2 + 1 1 = - * / 15 5 3 + 2 + 1 1 = - * 3 3 + 2 + 1 1 = - 9 + 2 + 1 1 = - 9 + 2 2 = - 9 4 = 5
Notación polaca en lógica
Jan Łukasiewicz también usó esta notación para la lógica. Aquí te mostramos cómo se escriben algunas ideas lógicas en notación polaca, junto con su significado y la palabra polaca de la que provienen:
| Concepto | Notación convencional |
Notación polaca |
Palabra polaca |
|---|---|---|---|
| Negación |  φ φ |
Nφ | negacja |
| Conjunción (Y) | φ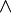 ψ ψ |
Kφψ | koniunkcja |
| Disyunción (O) | φ ψ ψ |
Aφψ | alternatywa |
| Condicional material (Si... entonces...) | φ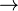 ψ ψ |
Cφψ | implikacja |
| Bicondicional (Si y solo si) | φ ψ ψ |
Eφψ | ekwiwalencja |
| Barra de Sheffer (Ni... ni...) | 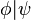 |
Dφψ | dysjunkcja |
| Posibilidad (Es posible que) |  φ φ |
Mφ | możliwość |
| Necesidad (Es necesario que) | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \Box</box>φ||Lφ||''konieczność'' |- |[[Cuantificador universal]] (Para todo)|| <math>\forall φ | Πφ | kwantyfikator ogólny |
| Cuantificador existencial (Existe al menos uno) | 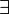 φ φ |
Σφ | kwantyfikator szczegółowy |
Notación polaca y las máquinas de pila
La notación polaca es muy útil para las máquinas que trabajan con una "pila" de datos. En estas máquinas, los operadores siempre van antes de los valores sobre los que actúan, y no se necesitan paréntesis.
- Ejemplo normal
Ejemplo 1: 2 * ( 3 + 5 ) Ejemplo 2: 2 * 3 + 5
- En notación polaca
Ejemplo 1: * 2 + 3 5 Ejemplo 2: + * 2 3 5
Véase también
 En inglés: Prefix notation Facts for Kids
En inglés: Prefix notation Facts for Kids
- Notación de infijo (la notación normal)
- Notación de postfijo, también llamada notación polaca inversa
- Lenguaje de programación LISP
- Expresión S


