Gran círculo para niños

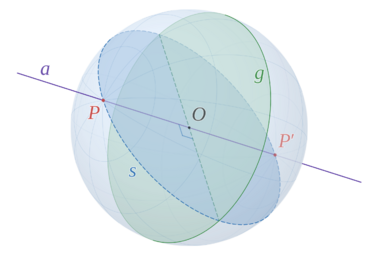
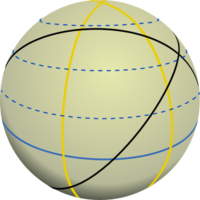
Un gran círculo, también llamado círculo mayor o círculo máximo, es un círculo que se forma cuando cortamos una esfera justo por su centro. Imagina que tienes una naranja y la cortas exactamente por la mitad: el borde del corte es un gran círculo. Este círculo tiene el mismo diámetro que la esfera.
La distancia más corta entre dos puntos en la superficie de una esfera siempre se encuentra siguiendo un arco de un gran círculo que los une. Piensa en un avión que viaja de un continente a otro: no vuela en línea recta sobre un mapa plano, sino que sigue una ruta curva que es parte de un gran círculo, porque esa es la forma más corta de llegar.
Los arcos de grandes círculos son como las "líneas rectas" en la superficie de una esfera. Para casi cualquier par de puntos diferentes en una esfera, solo hay un gran círculo que los conecta. Sin embargo, si los puntos están exactamente opuestos el uno del otro (como los polos Norte y Sur de la Tierra), hay infinitos grandes círculos que los unen. El camino más corto entre dos puntos en la superficie de una esfera es el arco más pequeño de un gran círculo que los une.
En contraste, un círculo pequeño en una esfera es el que se forma cuando cortamos la esfera con un plano que no pasa por su centro.
Contenido
¿Para qué sirven los círculos máximos?
Geometría y formas esféricas
En la geometría, los círculos máximos nos ayudan a entender cómo se comportan las distancias y las formas en superficies curvas como las esferas.
Triángulos en una esfera
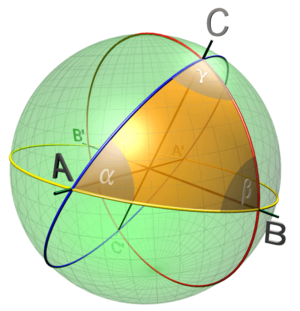
Si unimos tres puntos en la superficie de una esfera con arcos de grandes círculos que miden menos de 180 grados, formamos una figura llamada triángulo esférico. Los lados de este triángulo se miden como ángulos desde el centro de la esfera. En un triángulo esférico, la suma de sus tres ángulos siempre es mayor de 180 grados y menor de 540 grados.
Círculos máximos en la Tierra
En geografía y cartografía, los grandes círculos son muy importantes.
- Los meridianos (las líneas que van de polo a polo) son arcos de grandes círculos.
- El ecuador terrestre es el único gran círculo de latitud. Las otras líneas de latitud (los paralelos) son círculos pequeños, porque no pasan por el centro de la Tierra.
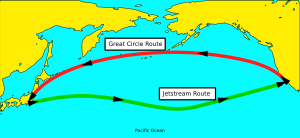
La trayectoria siguiendo una corriente en chorro (línea verde).
Los barcos y aviones usan rutas que siguen segmentos de grandes círculos para viajar la distancia más corta, siempre que el viento o las corrientes no los desvíen mucho. Por ejemplo, la duración de un vuelo entre dos aeropuertos se puede calcular usando la distancia de un gran círculo. A veces, para los aviones que viajan hacia el oeste en el hemisferio norte, la ruta más eficiente puede estar un poco al norte del gran círculo, y para los que van hacia el este, un poco al sur.
Cuando estas rutas de grandes círculos se muestran en un mapa plano (como los mapas de Mercator), a menudo se ven curvas. Esto es porque los mapas planos distorsionan la forma real de la Tierra. La ruta que parece una línea recta en un mapa plano en realidad es más larga que la ruta del gran círculo. Hay otros tipos de mapas, como la proyección gnomónica, donde los grandes círculos sí se ven como líneas rectas.
¿Cómo se usan los círculos máximos?
Los grandes círculos son muy útiles en la navegación. Por ejemplo, el horizonte celeste (la línea donde el cielo parece encontrarse con la Tierra), el ecuador celeste (la proyección del ecuador terrestre en el cielo) y la eclíptica (el camino aparente del Sol en el cielo) son ejemplos de grandes círculos en la esfera celeste.
Aunque la Tierra no es una esfera perfecta, los grandes círculos son una muy buena aproximación para calcular las rutas más cortas en la navegación aérea y marítima.
El ecuador de la Tierra es un gran círculo, y cualquier meridiano junto con su meridiano opuesto también forman un gran círculo. Un gran círculo siempre divide la Tierra en dos hemisferios. Si un gran círculo pasa por un punto, también pasará por el punto exactamente opuesto a él en la esfera (su punto antípoda).
Para la mayoría de los pares de puntos en la superficie de una esfera, hay un solo gran círculo que los une. La única excepción es cuando los puntos son antípodas (exactamente opuestos), en cuyo caso hay infinitos grandes círculos que los conectan. El arco más corto de un gran círculo entre dos puntos es el camino más corto en la superficie de la esfera.
Véase también
 En inglés: Great circle Facts for Kids
En inglés: Great circle Facts for Kids
- Trigonometría esférica
- Ortodrómica
- Loxodrómica
- Meridiano
- Paralelo
- Curso (navegación)
- Esfera celeste