Disyunción exclusiva para niños
Datos para niños Disyunción exclusiva |
||
|---|---|---|
 Diagrama de Venn de la conectiva
|
||
| Nomenclatura | ||
| Lenguaje natural | A o B pero no ambos | |
| Lenguaje formal |  |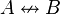
|
| Operador booleano |  |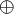
|
| Puerta lógica | ||
 |
||
| Tabla de verdad | ||
| Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{array}{c|c||c} A & B & A \nleftrightarrow B \ \hline V & V & F \ V & F & V \ F & V & V \ F & F & F \ \end{array} | ||
La disyunción exclusiva es un concepto importante en la lógica y las matemáticas. También se le conoce como "OR exclusivo" o "XOR". Imagina que tienes dos opciones y solo puedes elegir una de ellas, pero no ambas al mismo tiempo. Eso es lo que significa la disyunción exclusiva. Es un tipo especial de "o" que usamos para comparar dos ideas o afirmaciones.
Contenido
¿Qué es la Disyunción Exclusiva?
La disyunción exclusiva, o XOR, es una regla que nos dice cuándo una afirmación combinada es verdadera o falsa. Piensa en dos afirmaciones, A y B. La disyunción exclusiva de A y B solo es verdadera si A es verdadera y B es falsa, O si A es falsa y B es verdadera. Si ambas son verdaderas o ambas son falsas, entonces la disyunción exclusiva es falsa.
Para entenderlo mejor, podemos usar una tabla de verdad:
| Afirmación A | Afirmación B | A XOR B |
|---|---|---|
| Falso | Falso | Falso |
| Verdadero | Falso | Verdadero |
| Falso | Verdadero | Verdadero |
| Verdadero | Verdadero | Falso |
Aquí, "Verdadero" significa que la afirmación es cierta, y "Falso" significa que no lo es.
Diferencia con el "O" normal (Disyunción Inclusiva)
Es importante saber que la disyunción exclusiva es diferente del "o" que usamos normalmente, que se llama disyunción inclusiva.
- El "o" normal (inclusivo) es verdadero si al menos una de las afirmaciones es verdadera, o si ambas son verdaderas. Por ejemplo, "Voy al cine o leo un libro" es verdadero si vas al cine, si lees un libro, o si haces ambas cosas.
- La disyunción exclusiva (XOR) es verdadera solo si una de las afirmaciones es verdadera, pero no ambas. Por ejemplo, "Comeré una manzana o una pera" significa que comerás una, pero no las dos al mismo tiempo.
¿Para qué se usa la Disyunción Exclusiva?
Aunque la disyunción exclusiva no se usa tanto en la lógica diaria, es muy importante en el mundo de la informática y la tecnología.
- En la informática: Se usa en el Álgebra de Boole, que es la base de cómo funcionan los ordenadores.
- En la seguridad de la información: Es útil para crear y descifrar códigos secretos. Esto se debe a una propiedad especial: si aplicas XOR dos veces con la misma clave, recuperas la información original.
- En sistemas de almacenamiento de datos: Se utiliza en sistemas como RAID, que ayudan a guardar información de forma segura en varios discos duros. Si un disco falla, XOR permite reconstruir los datos perdidos.
Propiedades de la Disyunción Exclusiva
La disyunción exclusiva tiene algunas propiedades interesantes, como las operaciones matemáticas que conoces:
- Asociativa: No importa cómo agrupes las operaciones, el resultado es el mismo. Por ejemplo, (A XOR B) XOR C es igual a A XOR (B XOR C).
- Conmutativa: El orden de las afirmaciones no cambia el resultado. A XOR B es lo mismo que B XOR A.
- Su propia inversa: Si aplicas XOR a una afirmación consigo misma, el resultado es siempre falso. A XOR A es Falso.
- Distributiva: Se puede combinar con la operación "Y" (conjunción). Por ejemplo, A Y (B XOR C) es igual a (A Y B) XOR (A Y C).
Galería de imágenes
-
Símbolo de la puerta lógica XOR.
Véase también
En inglés: Exclusive disjunction Facts for Kids
- Álgebra booleana
- Puerta lógica
- Disyunción lógica
- Conjunción lógica
- Lógica proposicional
- Valor de verdad
- Operación matemática
- Cifrado XOR
