Puerta lógica para niños

Una puerta lógica o compuerta lógica es un dispositivo electrónico que funciona como un interruptor especial. Estas puertas toman una o más señales de entrada y producen una única señal de salida. Su funcionamiento se basa en reglas de Álgebra de Boole, que usan solo dos valores: 0 (apagado o falso) y 1 (encendido o verdadero).

Las compuertas lógicas son los bloques de construcción de todos los circuitos integrados modernos, como los que se encuentran en los chips de tu computadora o teléfono. Al combinar muchas de estas pequeñas puertas, se pueden crear sistemas muy complejos que realizan cálculos, almacenan información y controlan dispositivos.

Al principio, estas funciones se lograban con relés o interruptores electromagnéticos. Por ejemplo, para una compuerta "Y" (AND), se conectaban interruptores en circuito serie. Si uno estaba "abierto" (0), la salida era 0. Para una compuerta "O" (OR), se usaban interruptores en circuito paralelo.

Hoy en día, la microelectrónica permite que millones de transistores actúen como estos interruptores dentro de un pequeño circuito integrado. El cerebro de una computadora, la CPU, es un gran ejemplo de cómo se usan estas compuertas. Incluso se están investigando compuertas lógicas a nivel molecular para hacer los circuitos aún más pequeños.

Tipos de Compuertas Lógicas

Las compuertas lógicas se clasifican según la forma en que procesan las señales de entrada para producir una salida. Cada una tiene una regla específica.

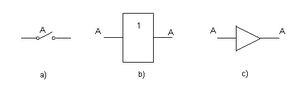
Compuerta SI o Buffer

La compuerta SI (también llamada buffer) es la más sencilla. Su función es simplemente pasar la señal de entrada a la salida sin cambiarla. Si la entrada es 0, la salida es 0. Si la entrada es 1, la salida es 1. Se usa a menudo para fortalecer una señal o para conectar diferentes partes de un circuito.

Símbolo de la función lógica SI

Su tabla de verdad muestra cómo funciona:

Tabla de verdad compuerta SI

Entrada	Salida
0	0
1	1

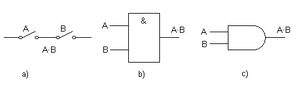
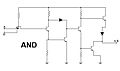
Compuerta Y (AND)

La compuerta Y (o AND) produce una salida de 1 solo si todas sus entradas son 1. Si alguna de sus entradas es 0, la salida será 0. Piensa en ella como una condición: "esto Y aquello deben ser verdaderos para que el resultado sea verdadero".

Símbolo de la función lógica Y

Su tabla de verdad para dos entradas (A y B) es:

Tabla de verdad compuerta AND

Entrada	Entrada	Salida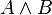
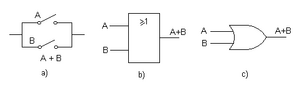
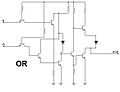
0	0	0
0	1	0
1	0	0
1	1	1

Compuerta O (OR)

La compuerta O (o OR) produce una salida de 1 si al menos una de sus entradas es 1. La salida solo será 0 si todas sus entradas son 0. Es como decir: "esto O aquello (o ambos) deben ser verdaderos para que el resultado sea verdadero".

Símbolo de la función lógica O

Su tabla de verdad para dos entradas (A y B) es:

Tabla de verdad compuerta OR

Entrada	Entrada	Salida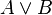
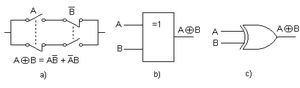
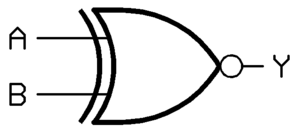
0	0	0
0	1	1
1	0	1
1	1	1

Compuerta O-Exclusiva (XOR)

La compuerta O-Exclusiva (o XOR) produce una salida de 1 si sus entradas son diferentes. Si las entradas son iguales (ambas 0 o ambas 1), la salida es 0. Piensa en ella como "esto O aquello, pero NO ambos".

Símbolo de la función lógica O-exclusiva

Su tabla de verdad para dos entradas (A y B) es:

Tabla de verdad compuerta XOR

Entrada	Entrada	Salida
0	0	0
0	1	1
1	0	1
1	1	0

Si tiene más de dos entradas, la compuerta XOR da una salida de 1 si el número de entradas en 1 es impar.

Lógica Negada

Las compuertas de lógica negada invierten el resultado de las compuertas directas.

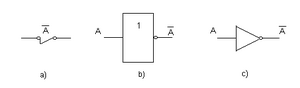
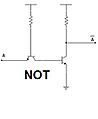
Compuerta NO (NOT)

La compuerta NO (o NOT) es un inversor. Toma una sola entrada y produce la salida opuesta. Si la entrada es 0, la salida es 1. Si la entrada es 1, la salida es 0.

Símbolo de la función lógica NO

Su tabla de verdad es:

Tabla de verdad compuerta NOT

Entrada	Salida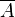
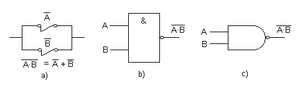
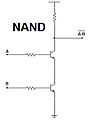
0	1
1	0

Compuerta NO-Y (NAND)

La compuerta NO-Y (o NAND) es como una compuerta AND seguida de una compuerta NOT. Su salida es 0 solo si todas sus entradas son 1. En cualquier otro caso, la salida es 1.

Símbolo de la función lógica NO-Y

Su tabla de verdad para dos entradas (A y B) es:

Tabla de verdad compuerta NAND

Entrada	Entrada	Salida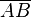
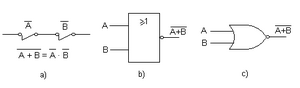
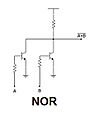
0	0	1
0	1	1
1	0	1
1	1	0

Compuerta NO-O (NOR)

La compuerta NO-O (o NOR) es como una compuerta OR seguida de una compuerta NOT. Su salida es 1 solo si todas sus entradas son 0. Si al menos una entrada es 1, la salida es 0.

Símbolo de la función lógica NO-O

Su tabla de verdad para dos entradas (A y B) es:

Tabla de verdad compuerta NOR

Entrada	Entrada	Salida
0	0	1
0	1	0
1	0	0
1	1	0

Compuerta NO-O Exclusiva (XNOR)

La compuerta NO-O Exclusiva (o XNOR) es el opuesto de la compuerta XOR. Su salida es 1 si sus entradas son iguales (ambas 0 o ambas 1). Si las entradas son diferentes, la salida es 0.

Símbolo de la compuerta lógica XNOR

Su tabla de verdad para dos entradas (A y B) es:

Tabla de verdad compuerta XNOR

Entrada	Entrada	Salida
0	0	1
0	1	0
1	0	0
1	1	1

Para más de dos entradas, la salida es 1 si el número de entradas en 1 es par.

Conjunto de Compuertas Lógicas Completo

Un conjunto de compuertas lógicas completo es un grupo de compuertas con el que se puede construir cualquier otra función lógica. Esto significa que, usando solo las compuertas de ese conjunto, podrías crear una compuerta AND, OR, NOT, o cualquier combinación que necesites.

Algunos ejemplos de conjuntos completos son:

• Compuertas AND, OR y NOT.
• Compuertas AND y NOT.
• Compuertas OR y NOT.
• ¡Solo la compuerta NAND!
• ¡Solo la compuerta NOR!

Es sorprendente que con solo las compuertas NAND o solo las compuertas NOR, se pueden construir todas las demás. Por eso se les llama "compuertas universales".

Galería de imágenes

• 

  Compuerta AND con transistores

• 

  Compuerta OR con transistores

• 

  Compuerta NOT con transistores

• 

  Compuerta NAND con transistores

• 

  Compuerta NOR con transistores