Distribución de Pareto para niños
Datos para niños Pareto |
||
|---|---|---|
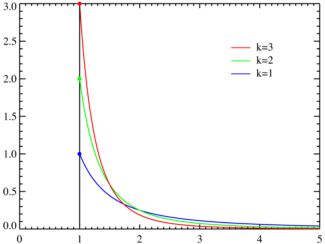 Funciones de densidad de probabilidad para diferentes α (k) con xm = 1. El eje horizontal es el parámetro x. Como α → ∞ la distribución se aproxima δ(x − xm) donde δ es la delta de Dirac. Función de densidad de probabilidad |
||
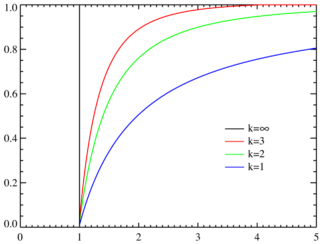 Funciones de densidad de distribución para diferentes α (k) con xm = 1. El eje horizontal es el parámetro x. Función de distribución de probabilidad |
||
| Parámetros | 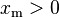 escala (real) escala (real)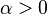 forma (real) forma (real) |
|
| Dominio | 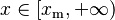 |
|
| Función de densidad (pdf) |
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{\alpha\,x_\mathrm{m}^\alpha}{x^{\alpha+1</td></tr><tr><td class="noprint" colspan="3" style="text-align:left;"></td></tr></table><!--IB_END-->\text{ for }x>x_m\! | cdf = La distribución de Pareto es una herramienta matemática que nos ayuda a entender cómo se reparten ciertas cosas en el mundo. Imagina que tienes un grupo de elementos y quieres saber cómo se distribuyen. Esta distribución nos muestra que, a menudo, una pequeña parte de esos elementos tiene la mayor cantidad de algo, mientras que la mayoría de los elementos tienen muy poco. Fue creada por un ingeniero, economista y sociólogo llamado Vilfredo Pareto. Él la usó para explicar cómo se distribuía la riqueza entre las personas. ContenidoLa Distribución de Pareto: ¿Qué es y para qué sirve?La distribución de Pareto es un tipo de distribución de probabilidad continua. Esto significa que se usa para describir eventos donde los resultados pueden ser cualquier número dentro de un rango, como la altura de las personas o la cantidad de lluvia. Se aplica en muchos campos, como la sociología, la geofísica y la economía. ¿Quién fue Vilfredo Pareto?Vilfredo Pareto fue un pensador italiano que vivió entre 1848 y 1923. Se interesó mucho en cómo funcionaba la sociedad y la economía. Observó que en muchos casos, una pequeña parte de la población poseía la mayor parte de la riqueza. Esta observación lo llevó a desarrollar la distribución que lleva su nombre. El Principio de Pareto o Regla del 80-20La idea principal de la distribución de Pareto se conoce a menudo como el Principio de Pareto o la Regla del 80-20. Esta regla dice que, en muchas situaciones, el 20% de las causas produce el 80% de los efectos. Por ejemplo, el 20% de los clientes de una empresa podría generar el 80% de sus ventas. O el 20% de tu ropa favorita es la que usas el 80% del tiempo. Es una forma sencilla de ver cómo las cosas no siempre se distribuyen de manera uniforme. ¿Dónde vemos la Distribución de Pareto en la vida real?La distribución de Pareto no solo se usa para hablar de la riqueza. Se ha visto que se aplica a muchos otros fenómenos. Aquí tienes algunos ejemplos:
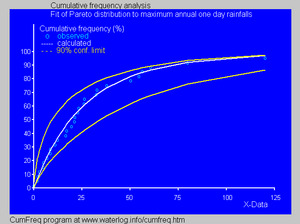
Herramientas para analizar datosExisten programas de computadora y software especiales que pueden ayudarte a ajustar una distribución de probabilidad, como la de Pareto, a un conjunto de datos. Esto permite a los expertos entender mejor cómo se comportan ciertos fenómenos y hacer predicciones. Galería de imágenesVéase también
|
|


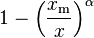 | mean =
| mean =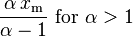 | median =
| median =![x_\mathrm{m} \sqrt[\alpha]{2}](/images/math/3/c/5/3c52a1728ced91e276d35d6e39be8ac3.png) | mode =
| mode =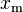 | variance =
| variance =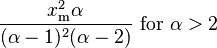 | skewness =
| skewness =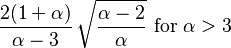 | kurtosis =
| kurtosis =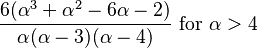 | entropy =
| entropy =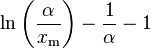 | mgf =No existe | char =
| mgf =No existe | char = 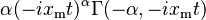 | fisher =
| fisher = 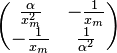 }}
}}

 En inglés:
En inglés: