Función de densidad de probabilidad para niños

Diagrama de caja y función de densidad de probabilidad de una distribución normal N(0, σ²).

En el mundo de la probabilidad, la función de densidad de probabilidad (a menudo llamada FDP o simplemente densidad) es una herramienta especial que nos ayuda a entender cómo se distribuyen las probabilidades para variables que pueden tomar cualquier valor dentro de un rango, como la altura de una persona o el tiempo que dura una batería.

Imagina que quieres saber la probabilidad de que una persona mida exactamente 1.65 metros. Para una variable continua como la altura, la probabilidad de un valor exacto es casi cero. En cambio, la FDP nos dice qué tan probable es que la variable caiga dentro de un rango específico de valores, por ejemplo, entre 1.64 y 1.66 metros.

La probabilidad de que una variable caiga en un rango determinado se calcula encontrando el "área" bajo la curva de la FDP en ese rango. Piensa en la FDP como una gráfica que muestra dónde es más probable que se encuentren los valores. Esta gráfica siempre es positiva o cero, y el área total debajo de toda la curva siempre suma 1, que representa el 100% de todas las posibilidades.

A veces, se usan otros nombres como "función de distribución de probabilidad", pero el término "función de densidad de probabilidad" es el más común y preciso para las variables continuas. Para las variables que toman valores específicos (como el número de caras al lanzar una moneda), se usa algo llamado "función de masa de probabilidad".

¿Qué es una Función de Densidad de Probabilidad?

Una función de densidad de probabilidad (FDP) nos ayuda a describir el comportamiento de una variable aleatoria continua. Nos dice qué tan probable es que esta variable tome un valor cercano a un punto específico.

Por ejemplo, si tenemos una variable aleatoria X (como la altura de los estudiantes), su FDP, que llamamos f_X, es una función que cumple dos cosas importantes:

• Siempre es mayor o igual a cero.
• Si sumamos (integramos) todos los valores de la función en todo su rango posible, el resultado es 1. Esto significa que la probabilidad total de que algo ocurra es del 100%.

La probabilidad de que la variable X esté entre dos valores, digamos a y b, se calcula como el área bajo la curva de f_X entre a y b.

Propiedades Clave de la FDP

Las funciones de densidad de probabilidad tienen propiedades importantes:

• La FDP, f_X(x), siempre es mayor o igual a 0 para cualquier valor de x. Esto significa que las probabilidades no pueden ser negativas.
• El área total bajo la curva de la FDP es siempre igual a 1. Esto representa que la suma de todas las probabilidades posibles es el 100%.
• La probabilidad de que la variable X tome un valor en un intervalo específico [a,b] es el área bajo la curva de la FDP en ese intervalo.

Ejemplos y Detalles Adicionales

A diferencia de las probabilidades que siempre están entre 0 y 1, una función de densidad de probabilidad puede tomar valores mayores que 1. Por ejemplo, si una variable se distribuye uniformemente en un rango muy pequeño (como entre 0 y 0.5), su densidad puede ser 2 en ese rango. Esto es porque la densidad se refiere a la "concentración" de probabilidad, no a la probabilidad directa de un punto.

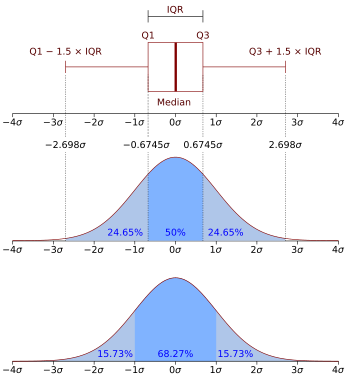
La distribución normal, que es muy común en la naturaleza (como la distribución de alturas o pesos), tiene una FDP con forma de campana.

No todas las distribuciones de probabilidad tienen una FDP. Las variables aleatorias discretas (como el número de veces que sale cara al lanzar una moneda) no tienen una FDP en el mismo sentido, ya que sus probabilidades se concentran en puntos específicos.

Si una distribución tiene una FDP, la probabilidad de que la variable tome un valor exacto es cero. Por ejemplo, la probabilidad de que una persona mida *exactamente* 1.7000000000 metros es cero, pero la probabilidad de que mida entre 1.69 y 1.71 metros sí se puede calcular.

Densidades para Múltiples Variables

Cuando tenemos varias variables aleatorias continuas al mismo tiempo (por ejemplo, la altura y el peso de una persona), podemos usar una función de densidad conjunta. Esta función nos dice la probabilidad de que todas esas variables caigan dentro de un rango específico en un espacio de varias dimensiones.

Por ejemplo, la probabilidad de que una persona mida entre 1.60 y 1.70 metros Y pese entre 50 y 60 kilogramos se calcularía usando esta función de densidad conjunta.

Densidad Marginal

Si tenemos una función de densidad conjunta para varias variables, podemos obtener la densidad marginal de una sola de esas variables. Esto significa que podemos "ignorar" las otras variables y ver cómo se distribuye solo una de ellas. Es como si tuviéramos un mapa de alturas y pesos, y quisiéramos ver solo la distribución de las alturas, sin importar los pesos.

Suma de Variables Aleatorias Independientes

Si tenemos dos variables aleatorias independientes (que no se afectan entre sí) y queremos saber la función de densidad de su suma, podemos combinar sus FDPs usando una operación matemática llamada "convolución". Esto nos da una nueva FDP para la suma de esas variables.

Familias de Densidades

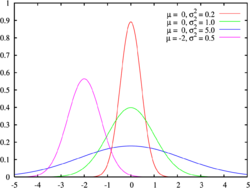
Muchas FDPs pertenecen a "familias" que se describen con parámetros. Por ejemplo, la distribución normal se define por dos parámetros: la media (el valor central) y la varianza (qué tan dispersos están los datos). Cambiando estos parámetros, podemos describir diferentes distribuciones normales, pero todas tienen la misma forma general de campana.

Estos parámetros son como "ajustes" que nos permiten adaptar la FDP a diferentes situaciones o conjuntos de datos, manteniendo la misma fórmula básica.

Ejemplo Práctico

Imagina que un tipo de bacteria vive normalmente entre 4 y 6 horas.

• La probabilidad de que una bacteria viva *exactamente* 5 horas es cero, porque el tiempo es una variable continua.
• Pero la probabilidad de que una bacteria viva entre 5 horas y 5.01 horas sí se puede calcular. Supongamos que es del 2% (0.02).
• Si el intervalo es más pequeño, por ejemplo, entre 5 horas y 5.001 horas (una décima parte del anterior), la probabilidad será aproximadamente una décima parte, es decir, 0.002.

En este caso, la relación (probabilidad de morir durante un intervalo) / (duración del intervalo) es aproximadamente constante. Si es 0.02 / 0.01 horas = 2 por hora, este valor de 2 horas^-1 es la densidad de probabilidad de morir alrededor de las 5 horas.

Esto significa que existe una función de densidad de probabilidad f donde f(5 horas) = 2 horas^-1. La integral de esta función f sobre cualquier período de tiempo nos dará la probabilidad de que la bacteria muera en ese período.

Función de densidad de probabilidad para la distribución normal.

Galería de imágenes

• 

  Diagrama de caja y función de densidad de probabilidad de una distribución normal.

• 

  Función de densidad de probabilidad para la distribución normal.

Véase también

En inglés: Probability density function Facts for Kids