Cuerpo (matemáticas) para niños
Un cuerpo en matemáticas es un tipo especial de conjunto de números o elementos donde puedes hacer sumas, restas, multiplicaciones y divisiones (excepto dividir por cero), ¡y estas operaciones se comportan de una manera muy ordenada y lógica! Piensa en los números que usas todos los días, como los números racionales (fracciones), los números reales (todos los números en la recta numérica) o los números complejos. Todos ellos son ejemplos de cuerpos.
Los cuerpos son muy importantes en muchas áreas de las matemáticas, como el álgebra abstracta, el análisis matemático y la teoría de números. Nos ayudan a entender cómo funcionan las operaciones matemáticas de forma más general. Por ejemplo, se usan para definir los espacios vectoriales y las matrices, que son herramientas clave en el álgebra lineal. También son fundamentales en la teoría de Galois, que estudia las relaciones de simetría en las ecuaciones.
Contenido
¿Qué es un cuerpo?
Un cuerpo es un conjunto de elementos, al que llamaremos K, donde se han definido dos operaciones: la suma (representada por +) y la multiplicación (representada por ·). Estas operaciones deben cumplir ciertas reglas, llamadas propiedades o axiomas:
Propiedades de un cuerpo
Para que un conjunto K sea un cuerpo, sus operaciones de suma y multiplicación deben seguir estas reglas:
Cierre
- Cuando sumas o multiplicas dos elementos de K, el resultado siempre debe estar también en K.
* Por ejemplo, si a y b están en K, entonces a + b y a · b también deben estar en K.
Asociatividad
- El orden en que agrupas los números para sumar o multiplicar no cambia el resultado.
* Para cualquier a, b, c en K: * a + (b + c) = (a + b) + c * a · (b · c) = (a · b) · c
Conmutatividad
- El orden de los números no cambia el resultado de la suma o la multiplicación.
* Para cualquier a, b en K: * a + b = b + a * a · b = b · a
Elementos neutros
- Existe un elemento especial para la suma, llamado cero (0), que no cambia ningún número al sumarlo.
* Para cualquier a en K: a + 0 = a.
- Existe un elemento especial para la multiplicación, llamado uno (1), que no cambia ningún número al multiplicarlo. Este 1 debe ser diferente de 0.
* Para cualquier a en K: a · 1 = a.
Elementos inversos
- Para cada elemento a en K, existe un opuesto (-a) tal que al sumarlos, el resultado es el cero.
* a + (-a) = 0.
- Para cada elemento a en K que no sea cero, existe un inverso multiplicativo (a-1) tal que al multiplicarlos, el resultado es el uno.
* a · a-1 = 1.
Distributividad
- La multiplicación se puede "distribuir" sobre la suma.
* Para cualquier a, b, c en K: a · (b + c) = (a · b) + (a · c).
Estas propiedades aseguran que las operaciones de resta y división (excepto por cero) siempre se puedan realizar dentro del cuerpo.
Reglas útiles
A partir de estas propiedades, podemos deducir otras reglas que ya conoces de la aritmética:
- El inverso de un producto es el producto de los inversos: (a·b)-1 = a-1 · b-1 (si a y b no son cero).
- -a = (-1) · a
- - (a · b) = (-a) · b = a · (-b)
- a · 0 = 0
Ejemplos de cuerpos
Números racionales
Los números racionales (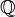 ) son todas las fracciones, como 1/2, -3/4, 5/1, etc. Este es un cuerpo porque puedes sumar, restar, multiplicar y dividir fracciones (excepto por cero) y el resultado siempre será otra fracción.
) son todas las fracciones, como 1/2, -3/4, 5/1, etc. Este es un cuerpo porque puedes sumar, restar, multiplicar y dividir fracciones (excepto por cero) y el resultado siempre será otra fracción.
Números reales
Los números reales (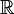 ) incluyen todos los números racionales y también los números irracionales (como
) incluyen todos los números racionales y también los números irracionales (como 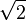 o
o  ). Con las operaciones de suma y multiplicación que conocemos, los números reales también forman un cuerpo.
). Con las operaciones de suma y multiplicación que conocemos, los números reales también forman un cuerpo.
Números complejos
Los números complejos (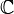 ) son números que se escriben como a + bi, donde a y b son números reales, e 'i' es la unidad imaginaria (un número especial que cumple que i2 = -1). Los números complejos también forman un cuerpo. Por ejemplo, para multiplicar:
) son números que se escriben como a + bi, donde a y b son números reales, e 'i' es la unidad imaginaria (un número especial que cumple que i2 = -1). Los números complejos también forman un cuerpo. Por ejemplo, para multiplicar:
- (a + bi)·(c + di) = ac + bci + adi + bdi2 = ac−bd + (bc + ad)i.
Cuerpos finitos
Existen cuerpos que tienen un número limitado de elementos. El cuerpo más pequeño tiene solo dos elementos: 0 y 1. Se le llama 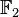 o
o 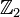 . Sus operaciones son:
. Sus operaciones son: 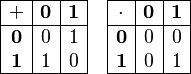 Este cuerpo es muy importante en la informática, la criptografía (para proteger información) y la teoría de la codificación (para enviar datos de forma segura).
Este cuerpo es muy importante en la informática, la criptografía (para proteger información) y la teoría de la codificación (para enviar datos de forma segura).
De manera más general, para cualquier número primo p, el conjunto de los números enteros "módulo p" (es decir, los restos al dividir por p) forma un cuerpo finito con p elementos. Se escribe como 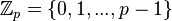 .
.
Cuerpos de funciones
También existen cuerpos formados por funciones. Por ejemplo, el conjunto de todas las funciones racionales (fracciones de polinomios) con coeficientes en un cuerpo dado, también forma un cuerpo.
Subcuerpos
Si tienes un cuerpo K, y un subconjunto E de K que también es un cuerpo con las mismas operaciones, entonces E es un subcuerpo de K. Por ejemplo, los números racionales (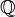 ) son un subcuerpo de los números reales (
) son un subcuerpo de los números reales (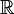 ).
).
Construcciones de cuerpos
Cuerpo de fracciones
A partir de un tipo especial de conjunto numérico llamado "dominio de integridad" (como los números enteros), se puede construir un cuerpo llamado su "cuerpo de fracciones". Por ejemplo, el cuerpo de los números racionales (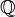 ) se construye a partir del anillo de los números enteros (
) se construye a partir del anillo de los números enteros (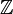 ).
).
Extensión de cuerpos
Una extensión de un cuerpo K es un cuerpo más grande que contiene a K y que se forma añadiendo las raíces de ciertos polinomios. Por ejemplo, los números complejos (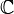 ) son una extensión de los números reales (
) son una extensión de los números reales (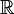 ), ya que se obtienen al añadir la raíz de la ecuación x2 + 1 = 0 (que es 'i').
), ya que se obtienen al añadir la raíz de la ecuación x2 + 1 = 0 (que es 'i').
Cuerpos con estructura adicional
Algunos cuerpos tienen propiedades extra que los hacen aún más interesantes:
Cuerpos ordenados
Un cuerpo es ordenado si puedes comparar sus elementos (decir si uno es mayor o menor que otro) de una manera que sea compatible con la suma y la multiplicación. Los números racionales y los números reales son cuerpos ordenados. Sin embargo, los números complejos no pueden ser ordenados de esta manera.
Cuerpos topológicos
Un cuerpo topológico es un cuerpo donde los elementos también forman un espacio topológico, lo que significa que puedes hablar de "cercanía" entre los elementos. Las operaciones de suma, multiplicación y sus inversas son "continuas", lo que significa que si los números de entrada están cerca, los resultados también lo estarán.
La "completación" de un cuerpo topológico es como "rellenar los huecos" en el cuerpo original. Por ejemplo, los números irracionales son "huecos" en los números racionales. Al "rellenar" esos huecos, obtenemos los números reales.
| Cuerpo | Métrica (distancia) | Completación | Ejemplo de secuencia que se acerca a cero |
|---|---|---|---|
| Q | | x − y | (valor absoluto usual) | R | 1/n |
|
Véase también
 En inglés: Field (mathematics) Facts for Kids
En inglés: Field (mathematics) Facts for Kids