Chiliágono para niños
Datos para niños Chiliágono |
||
|---|---|---|
 Un chiliágono regular
|
||
| Características | ||
| Tipo | Polígono regular | |
| Lados | 1000 | |
| Vértices | 1000 | |
| Grupo de simetría | 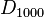 , orden 2x1000 , orden 2x1000 |
|
| Símbolo de Schläfli | {1000}, t{500}, tt{250}, ttt{125} (chiliágono regular) | |
| Diagrama de Coxeter-Dynkin | ||
| Polígono dual | Autodual | |
| Área | 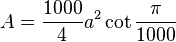 (lado  ) ) |
|
| Ángulo interior | 179.64° | |
| Propiedades | ||
| Convexo, isogonal, cíclico | ||
En geometría, un chiliágono es un polígono especial que tiene 1000 lados y 1000 vértices. Es una figura con muchísimos lados, lo que la hace parecerse mucho a un círculo si la dibujas.
Contenido
¿Qué es un Chiliágono?
Un chiliágono es un polígono con mil lados. La palabra "chiliágono" viene del griego, donde "chilioi" significa mil y "gon" significa ángulo.
Características de un Chiliágono Regular
Cuando un chiliágono es "regular", significa que todos sus lados miden lo mismo y todos sus ángulos interiores son iguales.
- Lados y vértices: Tiene exactamente 1000 lados y 1000 vértices (las esquinas).
- Ángulos interiores: Cada ángulo interior de un chiliágono regular mide 179.64 grados. Esto es muy cerca de 180 grados, que es el ángulo de una línea recta. Por eso, un chiliágono regular se ve casi como un círculo.
- Área: El área de un chiliágono regular es muy similar a la de un círculo que lo rodea. La diferencia es mínima, menos del 0.0004%.
¿Se puede dibujar un Chiliágono con regla y compás?
No, un chiliágono regular no se puede dibujar usando solo una regla y un compás. Esto se debe a una regla matemática que dice que solo ciertos polígonos con un número específico de lados pueden construirse de esta manera.
El Chiliágono en la Filosofía
Aunque es una figura geométrica, el chiliágono también ha sido usado por filósofos para explicar ideas importantes.
Pensar vs. Imaginar
El filósofo René Descartes usó el chiliágono como un ejemplo para mostrar la diferencia entre "entender" algo con la mente y "imaginar" algo.
- Imaginación: Descartes decía que cuando intentas imaginar un chiliágono, no puedes ver claramente los mil lados en tu mente. Tu imaginación crea una imagen borrosa, que no es muy diferente de la imagen de un polígono con 999 o 1001 lados.
- Entendimiento: Sin embargo, tu mente puede entender perfectamente lo que es un chiliágono. Sabes que tiene exactamente 1000 lados y puedes distinguirlo de otros polígonos, incluso si no puedes "verlo" claramente en tu imaginación.
Con este ejemplo, Descartes quería demostrar que nuestra capacidad de entender las cosas no depende solo de lo que podemos imaginar o ver.
Otros Filósofos y el Chiliágono
Otros pensadores también hablaron del chiliágono:
- Immanuel Kant y Gottfried Leibniz también usaron el chiliágono para explicar cómo podemos tener una idea clara de algo sin necesidad de tener una imagen mental perfecta de ello.
- Henri Poincaré lo usó para argumentar que la intuición (esa forma de entender las cosas sin un razonamiento consciente) no siempre se basa en lo que vemos o sentimos.
Simetría de un Chiliágono
Un chiliágono regular tiene mucha simetría. Esto significa que puedes girarlo o voltearlo de ciertas maneras y seguirá viéndose igual.
- Tiene 1000 líneas de simetría, lo que significa que puedes doblarlo por esas líneas y las dos mitades coincidirán perfectamente.
- También tiene simetría de rotación, lo que significa que puedes girarlo un poco y se verá igual que antes.
Chiliagrama: Una Estrella de Mil Puntas
Un chiliagrama es una estrella con 1000 puntas. Se forma conectando los vértices de un chiliágono de una manera especial.
- Existen muchas formas diferentes de chiliagramas, dependiendo de cómo se conecten los vértices.
- Algunos chiliagramas tienen puntas muy finas y se ven como patrones complejos.
Galería de imágenes
Véase también
 En inglés: Chiliagon Facts for Kids
En inglés: Chiliagon Facts for Kids