Unión de conjuntos para niños

La unión de los conjuntos A y B es otro conjunto A ∪ B que contiene todos los elementos de A y de B.

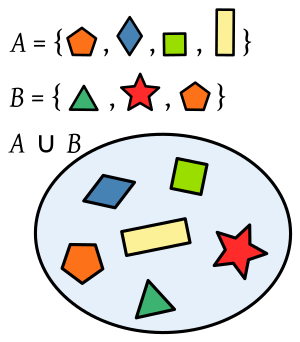
En el mundo de las matemáticas, especialmente en la teoría de conjuntos, la unión es una operación muy útil. Imagina que tienes dos grupos de cosas, como dos colecciones de juguetes. La unión de esos dos grupos sería una nueva colección que incluye todos los juguetes de ambos grupos, sin repetir ninguno.

Por ejemplo, si tenemos el grupo de los números naturales pares (2, 4, 6, ...) y el grupo de los números naturales impares (1, 3, 5, ...), la unión de estos dos grupos nos da el grupo de todos los números naturales (1, 2, 3, 4, ...).

El símbolo que usamos para la unión es ∪. Así, si llamamos al grupo de números pares P y al grupo de números impares I, podemos escribir:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbb{N} = P \cup I

Esto significa que el grupo de los números naturales (N) es la unión del grupo de los números pares (P) y el grupo de los números impares (I).

¿Qué es la Unión de Conjuntos?

La unión de dos grupos o conjuntos, digamos A y B, es un nuevo grupo que contiene todos los elementos que están en A, o en B, o en ambos. Es como juntar todo lo que tienes en dos cajas diferentes en una sola caja grande.

Por ejemplo, si el grupo A tiene los números {1, 2, 3, 4} y el grupo B tiene los números {5, 2, 1}, su unión sería {1, 2, 3, 4, 5}. Fíjate que los números 1 y 2, que estaban en ambos grupos, solo aparecen una vez en el grupo final. Esto es porque en los conjuntos, los elementos no se repiten.

Unión de dos conjuntos A o B.

Uniendo más de dos Conjuntos

Podemos unir no solo dos, sino muchos conjuntos. Si tienes varios grupos, por ejemplo, A₁, A₂, A₃, y así hasta A_n, la unión de todos ellos será un nuevo grupo que contiene todos los elementos de cada uno de esos grupos.

Por ejemplo, si tienes un grupo de frutas, otro de verduras y otro de lácteos, la unión de estos tres grupos sería un grupo que contiene todas las frutas, todas las verduras y todos los lácteos.

Propiedades de la Unión

La unión de conjuntos tiene algunas propiedades interesantes que nos ayudan a entender cómo funciona:

• Unir un conjunto consigo mismo: Si unes un grupo A con el mismo grupo A, el resultado es el mismo grupo A.

 :

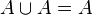
• Contener a los conjuntos originales: Los grupos originales A y B siempre son parte de su unión.

 :

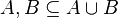
• Unir con un subconjunto: Si un grupo B ya está completamente dentro de otro grupo A (es un subconjunto), entonces la unión de A y B es simplemente A.

 :

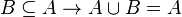
• Propiedad asociativa: No importa el orden en que unas tres o más grupos. El resultado siempre será el mismo.

 : Esto significa que puedes unir A con el resultado de unir B y C, o unir A y B primero y luego unir el resultado con C.

• Propiedad conmutativa: El orden de los grupos no cambia el resultado de la unión.

 : Es decir, unir A con B es lo mismo que unir B con A.

• Elemento neutro: El conjunto vacío (que no tiene ningún elemento, se representa con ∅) es como el "cero" de la unión. Si unes un grupo A con el conjunto vacío, el resultado es el mismo grupo A.

 :

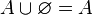
Unión e Intersección

La unión también se relaciona con otra operación llamada intersección (que es lo que tienen en común dos grupos). Hay unas reglas llamadas leyes distributivas:

• Si unes el grupo A con la intersección de B y C, es lo mismo que si primero unes A con B, y luego unes A con C, y finalmente encuentras la intersección de esos dos resultados.

 : Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A \cup (B \cap C) = (A \cup B) \cap (A \cup C)

• Si encuentras la intersección de A con la unión de B y C, es lo mismo que si primero encuentras la intersección de A con B, y luego la intersección de A con C, y finalmente unes esos dos resultados.

 : Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A \cap (B \cup C) = (A \cap B) \cup (A \cap C)

¿Cuántos Elementos hay en la Unión?

Cuando queremos saber cuántos elementos tiene la unión de dos grupos, debemos tener cuidado de no contar los elementos repetidos.

• Si los grupos no tienen elementos en común: Si los grupos A y B no comparten ningún elemento (se llaman disjuntos), entonces el número de elementos en su unión es simplemente la suma de los elementos de A y los elementos de B.

 : (El símbolo |A| significa "el número de elementos en el grupo A").

• Si los grupos tienen elementos en común: Si A y B comparten elementos, al sumar sus elementos por separado, estaríamos contando los elementos comunes dos veces. Para corregir esto, restamos el número de elementos que están en la intersección (los que tienen en común).

 : Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): |A \cup B| = |A| + |B| - |A \cap B| Por ejemplo, si A = {1, 2, 3} y B = {3, 4, 5}. |A| = 3, |B| = 3. La intersección A ∩ B = {3}, así que |A ∩ B| = 1. La unión A ∪ B = {1, 2, 3, 4, 5}, así que |A ∪ B| = 5. Usando la fórmula: 3 + 3 - 1 = 5. ¡Funciona!

Esta idea se puede extender para calcular el número de elementos cuando unes tres o más grupos, usando lo que se conoce como el principio de inclusión-exclusión.

El Axioma de la Unión

En la teoría axiomática de conjuntos, que es la base de cómo los matemáticos construyen los conjuntos, la existencia de la unión de conjuntos es tan fundamental que no se "demuestra", sino que se acepta como una regla básica o un axioma. Es como una de las reglas iniciales del juego de los conjuntos.

Galería de imágenes

• 

  La unión de los conjuntos A y B es otro conjunto A ∪ B que contiene todos los elementos de A y de B.

• 

  Unión de dos conjuntos A o B.

Véase también

• Álgebra de conjuntos
• Conjunto
• Teoría de conjuntos
• Intersección de conjuntos