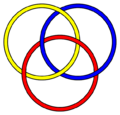
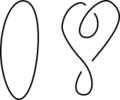Teoría de nudos para niños
La teoría de nudos es una parte de las matemáticas que estudia los nudos de una forma especial. Piensa en los cordones de tus zapatos, las cuerdas de un barco o incluso un cable enredado. Todos son ejemplos de nudos que vemos a diario.
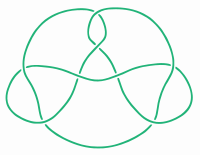
En matemáticas, un nudo es como una cuerda que ha sido atada y luego sus dos extremos se han unido para formar un círculo cerrado. Esto significa que no puedes desatarlo. El nudo más sencillo es un simple anillo, sin ningún cruce.
Los matemáticos estudian cómo se forman los nudos y cómo podemos saber si dos nudos son realmente el mismo, aunque se vean diferentes. Para esto, usan herramientas especiales que les ayudan a "describir" los nudos y compararlos.
Contenido
¿Qué es la Teoría de Nudos?
La teoría de nudos es una rama de la topología, que es una parte de las matemáticas que estudia las formas y los espacios. Se enfoca en entender los nudos matemáticos. Aunque se inspira en los nudos que usamos en la vida diaria, un nudo matemático tiene sus extremos unidos. Esto hace que no se pueda deshacer. El nudo más simple es un círculo sin cruces, al que llamamos "nudo trivial".
¿Qué es un Nudo Matemático?
Un nudo matemático es como un círculo que ha sido colocado en un espacio tridimensional. Imagina que tienes un aro de alambre. Ese es el nudo más simple. Si lo doblas y lo cruzas, pero luego unes sus puntas, tienes un nudo matemático.
Dos nudos matemáticos se consideran iguales si puedes transformar uno en el otro sin cortarlo ni pasarlo a través de sí mismo. Esto es como si tuvieras una cuerda anudada y pudieras moverla y estirarla en el aire hasta que se vea exactamente como otro nudo.
¿Cómo se Empezó a Estudiar los Nudos?
La gente ha usado nudos desde hace mucho tiempo, incluso antes de la historia escrita. Los usaban para guardar información, como los khipus, o para unir cosas. También les gustaban por su belleza y lo que simbolizaban. Por ejemplo, hay nudos muy antiguos en el arte chino y en el budismo tibetano. Los monjes celtas también crearon nudos muy complejos en libros antiguos como el Libro de Kells.
El estudio matemático de los nudos comenzó en el siglo XVIII con matemáticos como Alexandre-Théophile Vandermonde y Carl Friedrich Gauss. En el siglo XIX, un científico llamado Lord Kelvin pensó que los átomos podrían ser nudos formados por pequeñas corrientes. Esto llevó a Peter Guthrie Tait a hacer las primeras listas de nudos para clasificarlos. Aunque la idea de los átomos como nudos resultó ser incorrecta, el trabajo de Tait fue muy importante para el inicio de la teoría de nudos.
Más tarde, en el siglo XX, matemáticos como Max Dehn y James Waddell Alexander II estudiaron los nudos usando nuevas herramientas matemáticas. En las últimas décadas, la teoría de nudos ha encontrado aplicaciones en campos como el estudio del ADN y la construcción de ordenadores cuánticos.
¿Cuándo son Iguales Dos Nudos?
Un problema importante en la teoría de nudos es saber cuándo dos nudos son realmente el mismo. Imagina que tienes dos cuerdas anudadas. A simple vista, pueden parecer diferentes, pero quizás con un poco de movimiento y estiramiento, una se puede convertir en la otra.
En matemáticas, decimos que dos nudos son "equivalentes" si uno puede transformarse en el otro mediante movimientos suaves, sin cortar la cuerda ni hacer que se cruce a sí misma. Es como si pudieras mover el nudo en el espacio sin romperlo.
Existe un método para saber si dos nudos son iguales, pero a veces puede ser muy complicado y llevar mucho tiempo.
Dibujando Nudos: Diagramas y Movimientos
Para estudiar los nudos, los matemáticos suelen dibujarlos en un plano. A estos dibujos se les llama "diagramas de nudos". En un diagrama, se muestra cómo la cuerda se cruza a sí misma, indicando qué parte está por encima y cuál por debajo.
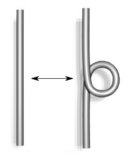
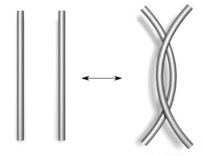
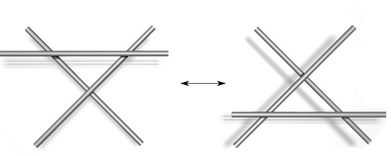
El mismo nudo puede tener muchos diagramas diferentes. Entonces, ¿cómo sabemos si dos diagramas representan el mismo nudo? En 1927, un matemático llamado Kurt Reidemeister descubrió que puedes transformar un diagrama de nudo en otro que represente el mismo nudo usando solo tres tipos de movimientos básicos. Estos se llaman "movimientos de Reidemeister":
Estos movimientos son muy útiles, pero no nos dicen cuántos movimientos se necesitan para transformar un diagrama en otro, ni si dos nudos no son equivalentes.
¿Cómo Distinguir Nudos? Los Invariantes
Para ayudar a distinguir los nudos, los matemáticos usan algo llamado "invariantes de nudos". Un invariante es una característica o "cantidad" que es la misma para todos los diagramas de un mismo nudo. Si calculas el invariante para dos nudos y obtienes valores diferentes, ¡sabes que son nudos distintos!
Algunos invariantes importantes son:
- La tricoloreabilidad: una forma de colorear el nudo con tres colores siguiendo ciertas reglas.
- El grupo de un nudo: una estructura matemática que describe cómo se "enreda" el espacio alrededor del nudo.
- Los polinomios de nudos: como el polinomio de Alexander o el polinomio de Jones, que son expresiones matemáticas que cambian según el nudo.
Estos invariantes son herramientas muy poderosas para clasificar y entender los nudos.
Nudos en Otras Dimensiones
Aunque normalmente pensamos en nudos en nuestro espacio tridimensional, los matemáticos también estudian nudos en dimensiones más altas. Por ejemplo, en un espacio de cuatro dimensiones, cualquier nudo hecho con un círculo puede deshacerse. Sin embargo, se pueden estudiar objetos más complejos, como esferas anudadas en espacios de más dimensiones. Esto ayuda a los matemáticos a entender mejor las formas y los espacios en general.
Galería de imágenes
-
Ejemplos de diferentes nudos, incluyendo el nudo trivial (arriba a la izquierda) y el nudo trébol (abajo).
-
Diagrama del nudo trébol, el nudo no trivial más sencillo
-
A la izquierda, el nudo deshecho y un nudo equivalente.
-
Puede resultar más difícil determinar si los nudos complejos, como el de la derecha, son equivalentes al nudo de deshacer.
-
Un enlace con tres componentes, cada uno de los cuales es un nudo trivial.
-
Friso formado por una 3-trenza
Véase también
En inglés: Knot theory Facts for Kids
- Enlace (teoría de nudos)
- Teoría de trenzas
- Los Quipus
- Cabuyería
