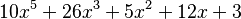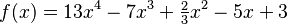Polinomio para niños

Enciclopedia para niños

En matemáticas, un polinomio es una expresión matemática formada por la suma de varios términos. Cada uno de estos términos se llama monomio.

Un monomio es el resultado de multiplicar:

Un número fijo, llamado coeficiente.
Una o varias variables (letras como "x", "y", "z").

Las variables pueden aparecer varias veces en un término, y en ese caso se escriben como una potencia. Por ejemplo, 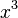$x^3$ significa Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x \cdot x \cdot x .

Cada monomio tiene un grado, que es la suma de los exponentes de sus variables. Por ejemplo, en el monomio 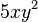$5xy^2$ , el exponente de x es 1 y el de y es 2. Sumando 1 + 2, el grado es 3.

El grado de un polinomio es el grado más alto de todos sus monomios.

Los polinomios son herramientas muy importantes en matemáticas y ciencias. Se usan para resolver problemas en física, química, economía y otras áreas. También son útiles para aproximar funciones complejas en cálculo.

Gráfica de una función polinomica de grado 7 en una variable.

Contenido

¿Qué es un polinomio?
Operaciones con polinomios
- Suma y resta de polinomios
- Multiplicación de polinomios
Funciones polinómicas
- Ejemplos de funciones polinómicas
Valor numérico de un polinomio
Factorización de polinomios
Historia de los polinomios
Proposiciones importantes sobre polinomios
Galería de imágenes
Véase también

¿Qué es un polinomio?

Los polinomios se construyen con un número limitado de variables y números fijos (coeficientes). Se usan las operaciones básicas de suma, resta y multiplicación, y las variables tienen exponentes que son números enteros positivos. Pueden tener una o varias variables.

Polinomios con una sola variable

Un polinomio con una sola variable, como x, se ve así:

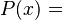
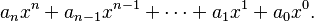
$P(x)_{}^{} =$ $a_n x^n + a_{n-1} x^{n - 1}+ \cdots + a_1 x^{1} + a_0 x^{0}.$

Aquí, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a_0, a_1, \ldots, a_n son los coeficientes (números).

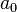$a_0$ es el término independiente (no tiene variable).
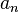$a_n$ es el coeficiente principal (el número que acompaña a la variable con el exponente más alto).

Si el coeficiente principal es 1, el polinomio se llama mónico.

Polinomios con varias variables

Los polinomios pueden tener más de una variable. Por ejemplo, los monomios Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 5xy o Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3xz^2 son parte de polinomios con varias variables.

Un ejemplo es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 4xy^2z . Este es un monomio con tres variables (x, y, z). Su coeficiente es 4, y los exponentes de x, y, z son 1, 2 y 1, respectivamente.

¿Cómo se calcula el grado de un polinomio?

El grado de un monomio es la suma de los exponentes de sus variables. El grado de un polinomio es el grado más alto de todos sus monomios. Se representa como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \text{gr}(p) .

Aquí tienes algunos ejemplos:

P(x) = 2: Es un polinomio de grado cero, porque solo tiene un término independiente.
P(x) = 3x + 2: Es un polinomio de grado uno.
P(x) = 3x² + 2x: Es un polinomio de grado dos.
P(x) = 2x³+ 3x + 2: Es un polinomio de grado tres.
P(x) = 4x⁴+ 4x + 2: Es un polinomio de grado cuatro.
P(x) = 2x⁵+ 3x + 1: Es un polinomio de grado cinco.

El polinomio nulo (o cero) es aquel donde todos sus coeficientes son cero. Su grado se define como 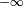$\scriptstyle -\infty$ .

Operaciones con polinomios

Podemos sumar, restar y multiplicar polinomios.

Suma y resta de polinomios

Para sumar o restar polinomios, agrupamos los términos que tienen las mismas variables con los mismos exponentes y luego los simplificamos.

Multiplicación de polinomios

Para multiplicar polinomios, multiplicamos cada término de un polinomio por cada término del otro. Después, simplificamos los términos semejantes.

Ejemplo de multiplicación

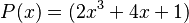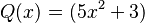Sean los polinomios: $P(x) = (2x_{}^3+4x+1)$ y $Q(x)_{}^{} = (5x^2+3)$ . El producto es:

P(x)Q(x)_{}^{} =

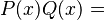Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (2x_{}^3+4x+1)(5x^2+3)

Multiplicamos cada parte:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (2x_{}^3+4x+1)(5x^2) + (2x^3+4x+1)(3)

Esto nos da:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (10x_{}^5 + 20x^3 + 5x^2) + (6x^3+12x+3)

Finalmente, sumamos los términos semejantes:

10x_{}^5 + 26x^3 + 5x^2 + 12x + 3

Una regla importante es que el grado del producto de dos polinomios es la suma de sus grados.

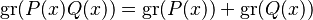
(*) $\mbox{gr}(P(x)Q(x)) = \mbox{gr}(P(x)) + \mbox{gr}(Q(x))\,$

Funciones polinómicas

Una función polinómica es una función matemática que se define usando un polinomio. Simplemente, sustituimos la variable del polinomio por un número para obtener un resultado.

Las funciones polinómicas son muy útiles porque son fáciles de calcular y se usan para aproximar funciones más complicadas en análisis numérico.

Ejemplos de funciones polinómicas

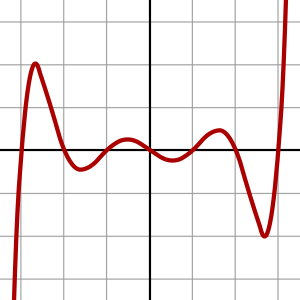
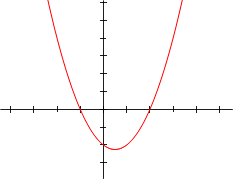
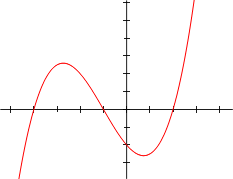
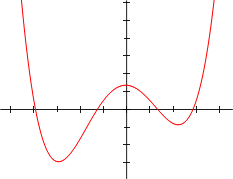
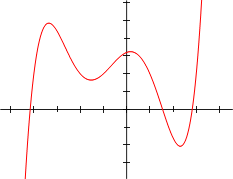
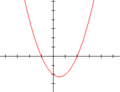
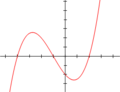
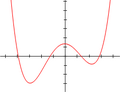
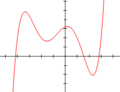
Las gráficas que ves a continuación muestran cómo se ven las funciones polinómicas. Recuerda que un polinomio es la expresión, y la función polinómica es lo que obtenemos al darle valores a la variable y graficar los resultados.

Polinomio de grado 2: f(x) = x² - x - 2= (x+1)(x-2).	Polinomio de grado 3: f(x) = x³/5 + 4x²/5 - 7x/5 - 2= 1/5 (x+5)(x+1)(x-2).
Polinomio de grado 4: f(x) = 1/14 (x+4)(x+1)(x-1)(x-3) + 0.5.	Polinomio de grado 5: f(x) = 1/20 (x+4)(x+2)(x+1)(x-1)(x-3) + 2.

Un ejemplo de función polinómica de cuarto grado es:

f(x)= 13x^4 - 7x^3 + \begin{matrix}\frac{2}{3}\end{matrix} x^2 - 5x + 3

Aquí, el coeficiente principal es 13 y el término independiente es 3.

Valor numérico de un polinomio

El valor numérico de un polinomio 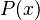$P(x)$ para un número específico, digamos $x=a$ , se obtiene al reemplazar la variable x por ese número y realizar todas las operaciones. El resultado se llama 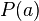$P(a)$ .

Por ejemplo, si tenemos 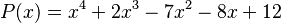$P(x) = x^4 + 2x^3 - 7x^2 - 8x + 12$ , para encontrar su valor cuando $x = 3$ , hacemos:

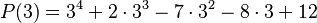
$P(3) = 3^4 + 2 \cdot 3^3 - 7 \cdot 3^2 - 8 \cdot 3 + 12$

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): P(3) = 81 + 2 \cdot 27 - 7 \cdot 9 - 24 + 12

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): P(3) = 81 + 54 - 63 - 24 + 12

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): P(3) = 147 - 87 + 12

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): P(3) = 60 + 12

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): P(3) = 72

Si al sustituir un valor a en el polinomio, el resultado es cero (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): P(a) = 0 ), entonces a se llama una raíz del polinomio. Esto significa que $(x - a)$ es un factor del polinomio.

Factorización de polinomios

Factorizar un polinomio significa escribirlo como una multiplicación de polinomios más simples.

Por ejemplo, el polinomio Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x^2 - 2 se puede factorizar como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (x + \sqrt{2})(x - \sqrt{2}) .

Historia de los polinomios

La idea de resolver ecuaciones con polinomios es muy antigua. Ya en el papiro de Moscú (alrededor del 1890 a.C.), un texto egipcio, se encuentra un problema que se resuelve con una fórmula polinómica.

La forma en que escribimos los polinomios hoy en día se desarrolló a partir del siglo XV.

Algunos polinomios, como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): P(x) = x^2 + 1 , no tienen raíces que sean números reales. Sin embargo, si consideramos los números complejos, ¡todo polinomio (que no sea una constante) tiene al menos una raíz! Esto es lo que dice el teorema fundamental del álgebra.

Durante mucho tiempo, los matemáticos buscaron fórmulas para encontrar las raíces de polinomios de diferentes grados. Se encontraron fórmulas para polinomios de hasta cuarto grado en el siglo XVI. Pero, para polinomios de quinto grado o mayores, fue mucho más difícil. En 1824, el matemático Niels Henrik Abel demostró que no existen fórmulas generales para resolver polinomios de quinto grado o más. Este descubrimiento fue muy importante y dio origen a la teoría de Galois.

Proposiciones importantes sobre polinomios

Teorema del resto (o de Bezout)

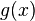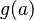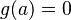Este teorema dice que si divides un polinomio $g(x)$ entre $(x-a)$ , el resto de esa división es igual a $g(a)$ . Si $g(a)=0$ , entonces a es una raíz del polinomio.

Ejemplo: Si Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): g(x) = x^4 -5x^3 + 5x^2-1 , y calculamos Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): g(1) :

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): g(1) = 1^4 - 5(1)^3 + 5(1)^2 - 1 = 1 - 5 + 5 - 1 = 0 . Como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): g(1) = 0 , el número 1 es una raíz de 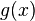$g(x)$ .

Teorema fundamental del álgebra

Este teorema establece que cualquier polinomio (que no sea una constante) siempre tiene al menos una raíz, que puede ser un número real o un número complejo.

Teorema de los factores lineales

Este teorema nos dice que un polinomio de grado n se puede escribir como la multiplicación de n factores lineales (de la forma Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x-r_i ) y el coeficiente principal del polinomio.

Galería de imágenes

Polinomio de grado 2: f(x) = x² - x - 2= (x+1)(x-2).
Polinomio de grado 3: f(x) = x³/5 + 4x²/5 - 7x/5 - 2=
1/5 (x+5)(x+1)(x-2).
Polinomio de grado 4: f(x) = 1/14 (x+4)(x+1)(x-1)(x-3) + 0.5.
Polinomio de grado 5: f(x) = 1/20 (x+4)(x+2)(x+1)(x-1)(x-3) + 2.

Véase también

En inglés: Polynomial Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Polinomio&oldid=5007835»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Polinomio para Niños. Enciclopedia Kiddle.