Proceso adiabático para niños
Un proceso adiabático es un cambio que ocurre en un sistema (como un gas o un líquido) donde no hay intercambio de calor con el ambiente que lo rodea. Imagina que tienes una botella térmica muy buena: si pones algo caliente dentro, el calor no sale; si pones algo frío, el calor no entra. Eso es una idea de lo que significa "adiabático": un aislamiento perfecto del calor.
Cuando un proceso adiabático es además "reversible" (lo que significa que puede volver a su estado original sin dejar cambios en el entorno), se le llama proceso isoentrópico. Por otro lado, si hay un intercambio máximo de calor y la temperatura se mantiene constante, se llama proceso isotérmico.
La palabra "adiabático" viene de una palabra griega que significa "impenetrable". Una pared muy bien aislada se parece mucho a un límite adiabático. Otro ejemplo es la temperatura que alcanza una llama si no pierde calor al ambiente. En los sistemas de aire acondicionado, algunos procesos para añadir humedad al aire son adiabáticos, porque no hay intercambio de calor, aunque la temperatura y la humedad del aire cambien.
El calentamiento y enfriamiento adiabático ocurren a menudo cuando cambia la presión de un gas. Esto hace que su volumen y temperatura también cambien. Podemos entender estos cambios usando la ley de los gases ideales.
Según la primera ley de la termodinámica, la energía interna de un sistema (su energía guardada) cambia si se realiza un trabajo sobre él o por él, siempre que no haya intercambio de calor. Si un sistema realiza trabajo, lo hace usando su propia energía interna, ya que no recibe calor de fuera.
Cuando hablamos de ondas, los procesos adiabáticos solo se dan en las ondas longitudinales.
Contenido
¿Qué es un proceso adiabático?
Un proceso se considera adiabático cuando no hay transferencia de calor hacia o desde un sistema. Esto significa que la cantidad de calor (Q) es igual a cero. Se dice que un sistema que experimenta un proceso adiabático está "adiabáticamente aislado".
A menudo, se simplifica la realidad y se asume que un proceso es adiabático. Por ejemplo, cuando un gas se comprime muy rápido dentro del cilindro de un motor, se considera que ocurre tan deprisa que casi no hay tiempo para que el calor se escape al exterior. Aunque los cilindros no están perfectamente aislados, para entender el proceso, se idealiza como adiabático. Lo mismo ocurre cuando el gas se expande.
Esta idea de aislamiento adiabático es muy útil para hacer cálculos y entender cómo se comportan los sistemas. Por ejemplo, el científico Pierre-Simon Laplace explicó que cuando el sonido viaja a través de un gas, no hay tiempo para que el calor se mueva, por lo que la propagación del sonido es un proceso adiabático.
Aplicaciones de la suposición adiabática
La primera ley de la termodinámica nos dice que el cambio en la energía interna de un sistema es igual al calor que se le añade menos el trabajo que el sistema realiza.
- Si un sistema tiene paredes muy rígidas que no permiten que se realice trabajo (W=0), y se le añade calor, su temperatura aumentará.
- Si las paredes son rígidas y no permiten trabajo, pero están aisladas (Q=0), y se le añade energía en forma de trabajo (como al agitar un líquido viscoso), la temperatura del sistema también aumentará.
- Si las paredes están aisladas (Q=0) pero no son rígidas, y se añade energía al sistema realizando trabajo (como al comprimir un gas sin fricción), la temperatura del sistema aumentará. Este proceso ideal se llama proceso isoentrópico y se considera "reversible". Si se invirtiera, la energía podría recuperarse.
En la naturaleza, los procesos adiabáticos reales no son perfectos y siempre hay algo de fricción o disipación de energía, lo que los hace "irreversibles".
Calentamiento y enfriamiento adiabáticos
Cuando un gas se comprime de forma adiabática, su temperatura aumenta. Por el contrario, cuando un gas se expande de forma adiabática, su temperatura disminuye.
¿Cómo funciona el calentamiento adiabático?
El calentamiento adiabático ocurre cuando la presión de un gas aumenta porque el entorno realiza trabajo sobre él. Un ejemplo claro es lo que sucede en los motores diésel: un pistón comprime el gas dentro de un cilindro tan rápidamente que el calor no tiene tiempo de escapar. Esto eleva la temperatura del combustible lo suficiente como para que se encienda sin necesidad de una chispa.
También vemos el calentamiento adiabático en la atmósfera terrestre. Cuando una masa de aire desciende (por ejemplo, en vientos como el viento foehn o el viento Chinook que bajan por una montaña), su presión aumenta. Al aumentar la presión, el volumen del aire disminuye y su temperatura sube. Esto ocurre porque se está realizando trabajo sobre esa masa de aire, lo que aumenta su energía interna. Como el aire solo puede liberar calor lentamente, se considera que está aislado adiabáticamente.
¿Cómo funciona el enfriamiento adiabático?
El enfriamiento adiabático ocurre cuando la presión sobre un sistema aislado disminuye, permitiéndole expandirse y realizar trabajo sobre su entorno. Cuando la presión sobre una masa de gas se reduce, el gas se expande. A medida que el volumen aumenta, la temperatura baja porque su energía interna disminuye.
Este tipo de enfriamiento se observa en la atmósfera cuando el aire asciende, como en las montañas (elevación orográfica) o en las ondas de sotavento. Este enfriamiento puede llevar a la formación de pileus o nubes lenticulares. De hecho, el enfriamiento adiabático en zonas montañosas es una de las razones por las que a veces nieva en partes del desierto del Sáhara.
El enfriamiento adiabático no solo ocurre con gases. Una técnica para alcanzar temperaturas extremadamente bajas (cercanas al cero absoluto) es la desmagnetización adiabática. En este proceso, se cambia el campo magnético de un material magnético para lograr un enfriamiento adiabático. Incluso el universo en expansión puede describirse como un fluido que se enfría adiabáticamente.
En la práctica, ningún proceso es perfectamente adiabático. Siempre hay alguna pérdida de calor, ya que no existen aislantes perfectos. Sin embargo, muchos procesos se aproximan a ser adiabáticos porque la transferencia de calor es muy lenta en comparación con la duración del proceso.
Representación gráfica de las curvas adiabáticas
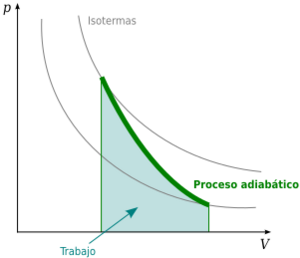
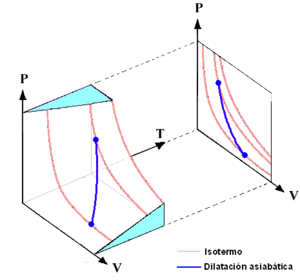
Las curvas adiabáticas se pueden dibujar en un gráfico que muestra la presión (P) y el volumen (V) de un gas. Estas curvas tienen algunas características interesantes:
- Se acercan mucho a los ejes del gráfico, pero nunca los tocan.
- Cada curva adiabática se cruza con cada curva de temperatura constante (isotermas) en un solo punto.
- Una curva adiabática se parece a una isoterma, pero es más inclinada (más vertical) porque durante una expansión, un proceso adiabático pierde más presión que uno isotérmico.
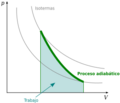
Cálculo del trabajo en un proceso adiabático
Para un gas ideal en un proceso adiabático reversible, la relación entre la presión (P) y el volumen (V) se describe con una fórmula especial: P Vγ = constante Aquí, P es la presión, V es el volumen, y γ (gamma) es el coeficiente adiabático. Este coeficiente es una relación entre el calor específico del gas a presión constante y a volumen constante.
Por ejemplo, para un gas ideal con un solo átomo (monoatómico), γ es 5/3. Para un gas con dos átomos (diatómico), como el nitrógeno o el oxígeno (que son los principales componentes del aire), γ es aproximadamente 7/5 o 1.4.
Como no hay calor que entre o salga del sistema, cualquier trabajo que se realice se hace a expensas de la energía interna del gas.
Enfriamiento adiabático del aire en la atmósfera
Cuando hablamos del enfriamiento adiabático del aire, hay tres conceptos importantes:
- La tasa ambiente de la atmósfera: Es la velocidad a la que el aire se enfría a medida que se gana altitud.
- La tasa seca adiabática: Es de aproximadamente -1°C por cada 100 metros de subida. Se aplica al aire que no está saturado de vapor de agua.
- La tasa húmeda adiabática: Es de aproximadamente -0.6°C a -0.3°C por cada 100 metros de subida. Se aplica al aire que ya ha alcanzado su punto de rocío (está saturado de vapor de agua).
La primera tasa describe la temperatura del aire que rodea una masa de aire que está subiendo. Las otras dos tasas se refieren a cómo se enfría la propia masa de aire a medida que asciende. El enfriamiento adiabático es una de las principales razones por las que se forman las nubes.
Galería de imágenes
Véase también
 En inglés: Adiabatic process Facts for Kids
En inglés: Adiabatic process Facts for Kids
- Motor adiabático
- Pistón de fuego
- Criterio de signos termodinámico
- Proceso termodinámico
- Sistema termodinámico