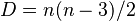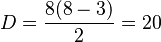Octógono para niños
Datos para niños Octágono |
||
|---|---|---|
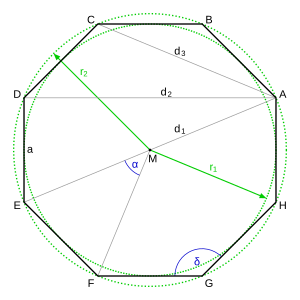
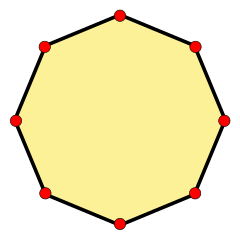 Un octágono regular
|
||
| Características | ||
| Tipo | Polígono regular | |
| Lados | 8 | |
| Vértices | 8 | |
| Grupo de simetría | 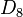 , orden 2x8 , orden 2x8 |
|
| Símbolo de Schläfli | {8}, t{4} (octágono regular) | |
| Diagrama de Coxeter-Dynkin | ||
| Polígono dual | Autodual | |
| Área | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A = 2(1+\sqrt{2})a^2 \simeq 4.83a^2 (lado  ) ) |
|
| Ángulo interior | 135° | |
| Propiedades | ||
| Convexo, isogonal, cíclico | ||
Un octágono u octógono es una figura geométrica plana que tiene ocho lados rectos y ocho esquinas (llamadas vértices). Es una forma común que puedes ver en muchas señales de tráfico o en el diseño de edificios.
Contenido
Propiedades del Octágono
Un octágono, sin importar si es regular o irregular, tiene algunas características que siempre se cumplen.
¿Cuántas diagonales tiene un octágono?
Un octágono tiene 20 diagonales. Una diagonal es una línea que conecta dos esquinas (vértices) que no están unidas por un lado. Puedes calcular el número de diagonales de cualquier polígono usando la fórmula:
Donde n es el número de lados del polígono. Para un octágono, n es 8, así que:
¿Cuál es la suma de los ángulos interiores de un octágono?
La suma de todos los ángulos interiores de cualquier octágono siempre es 1080 grados. Esto es cierto para todos los octágonos, ya sean regulares o irregulares.
Octágono Regular: Lados y Ángulos Iguales
Un octágono regular es especial porque todos sus ocho lados miden lo mismo y todos sus ocho ángulos también son iguales (congruentes).
Medida de los ángulos en un octágono regular
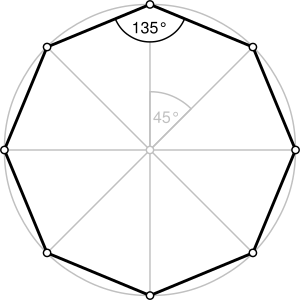
Cada ángulo interior de un octágono regular mide 135 grados. Esto significa que si mides las esquinas de un octágono regular, todas serán idénticas. Cada ángulo exterior (el ángulo que se forma al extender uno de los lados) de un octágono regular mide 45 grados.
Calcular el perímetro de un octágono regular
El perímetro es la medida de todo el contorno de una figura. Para encontrar el perímetro P de un octágono regular, solo tienes que multiplicar la longitud t de uno de sus lados por ocho (ya que tiene ocho lados iguales):
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): P = 8\cdot t
Si conoces la apotema (la distancia desde el centro del polígono hasta el punto medio de uno de sus lados) a, el perímetro se puede calcular con esta fórmula:
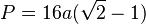
Calcular el área de un octágono regular
El área A de un octágono regular es el espacio que ocupa dentro de sus límites. Si conoces la longitud del lado t, puedes usar esta fórmula:
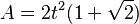
Si conoces la apotema a del octágono, otra forma de calcular el área es:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A = 8\cdot a^2 \cdot \tan(\pi/8) \simeq a^2 \cdot 3.31371
También, si conoces el perímetro P y la apotema a, el área es:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A = \frac{P\cdot a}{2}
El símbolo de Schläfli para un octágono regular es {8}. Este símbolo se usa en geometría para describir polígonos y poliedros regulares.
Octágono Irregular: Lados y Ángulos Diferentes
Un octágono irregular es una figura plana que también tiene ocho lados, pero a diferencia del regular, sus lados pueden tener diferentes longitudes y sus ángulos pueden ser desiguales. Esto significa que hay muchísimas formas diferentes de octágonos irregulares.
Calcular el perímetro de un octágono irregular
Para encontrar el perímetro P de un octágono irregular, simplemente sumas la longitud de cada uno de sus ocho lados:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): P = L_1 + L_2+L_3+L_4+L_5+L_6+L_7+L_8
Donde L1, L2, ..., L8 son las longitudes de cada lado del octágono.
Calcular el área de un octágono irregular
Para calcular el área de un octágono irregular, una forma común es dividirlo en ocho triángulos más pequeños. Luego, calculas el área de cada triángulo por separado y sumas todas esas áreas. La fórmula para el área de un triángulo es:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A = \frac {base \cdot altura}{2}
Después de calcular el área de cada uno de los ocho triángulos, las sumas para obtener el área total del octágono irregular.
Véase también
 En inglés: Octagon Facts for Kids
En inglés: Octagon Facts for Kids