Infinito para niños
El concepto de infinito (símbolo: ∞) se refiere a algo que no tiene límite ni final. Es lo opuesto a lo finito, que sí tiene un final o un límite. Esta idea aparece en diferentes áreas como las matemáticas, la filosofía y la astronomía.
En matemáticas, el infinito se usa de varias maneras. Por ejemplo, en geometría, existe el punto al infinito o el punto de fuga. En el análisis matemático, se habla de límites al infinito, que describen el comportamiento de funciones cuando los números se hacen muy, muy grandes. También, en la teoría de conjuntos, existen los números transfinitos, que son formas de contar elementos en conjuntos infinitos.
Contenido
¿Qué es un conjunto infinito?
En matemáticas, un conjunto es una colección de elementos. Un conjunto es finito si podemos contar todos sus elementos y llegar a un número. Por ejemplo, el conjunto de las frutas {manzana, pera, durazno} es finito y tiene 3 elementos.
Un conjunto es infinito si no podemos terminar de contar sus elementos. Una característica especial de los conjuntos infinitos es que pueden tener la misma cantidad de elementos que una parte de sí mismos. Esto suena extraño, ¡pero es lo que los hace infinitos!
¿Cómo se comparan los tamaños de los conjuntos?
Para saber si dos conjuntos tienen la misma cantidad de elementos, usamos algo llamado biyección. Imagina que tienes dos grupos de cosas y puedes emparejar cada cosa de un grupo con una cosa del otro grupo, sin que sobre nada en ninguno de los dos. Si puedes hacer eso, entonces ambos grupos tienen la misma cantidad de elementos.
Por ejemplo, si tienes el conjunto {manzana, pera, durazno} y el conjunto {0, 1, 2}, puedes emparejarlos así:
- Manzana con 0
- Pera con 1
- Durazno con 2
Como puedes hacer estas parejas "uno a uno", decimos que ambos conjuntos tienen la misma cantidad de elementos, o la misma cardinalidad.
El primer conjunto infinito
El matemático Georg Cantor fue quien dio una definición clara de conjunto infinito. Él observó que un conjunto es infinito si puedes encontrar una parte de ese conjunto que, aunque sea más pequeña, tiene la misma cantidad de elementos que el conjunto original.
Pensemos en los números naturales N = {1, 2, 3, 4, 5, ...}. Este es un conjunto infinito. Ahora, tomemos solo los números pares P = {2, 4, 6, 8, 10, ...}. El conjunto P es una parte de N.
¿Podemos emparejar cada número natural con un número par? ¡Sí! Podemos usar la regla de que a cada número natural n le corresponde el número par 2n.
- 1 se empareja con 2
- 2 se empareja con 4
- 3 se empareja con 6
- 4 se empareja con 8
...y así sucesivamente.
Esto significa que, aunque el conjunto de los números pares es solo una parte de los números naturales, ¡ambos tienen la misma cantidad de elementos! Por eso, el conjunto de los números naturales es un conjunto infinito.
Números ordinales infinitos
Los números ordinales nos ayudan a indicar la posición de algo en una lista ordenada (primero, segundo, tercero...). Los números naturales (0, 1, 2, 3...) son un ejemplo de ordinales finitos.
El primer número ordinal infinito se llama omega (ω). Representa el conjunto de todos los números naturales. Imagina una lista que nunca termina: 0, 1, 2, 3, ...ω. El omega es como el "final" de esa lista infinita de números naturales.
Después de omega, podemos tener ω+1, ω+2, y así. Esto significa que podemos seguir añadiendo elementos después de la infinidad de números naturales. Curiosamente, en los números ordinales, el orden importa mucho. Por ejemplo, ω+1 no es lo mismo que 1+ω. Esto es diferente a como sumamos los números normales, donde 2+3 es lo mismo que 3+2.
Números cardinales infinitos
Los números cardinales nos dicen cuántos elementos tiene un conjunto. Es diferente de los ordinales, que nos dicen la posición. Por ejemplo, "cinco" es un cardinal, mientras que "quinto" es un ordinal.
El cardinal del conjunto de los números naturales (ω) se llama álef-cero (ℵ₀). Es el cardinal infinito más pequeño.
Existen otros cardinales infinitos más grandes. Por ejemplo, el conjunto de todos los números reales (que incluyen decimales, fracciones, etc.) tiene un cardinal mayor que ℵ₀. Se le llama el cardinal del continuo.
Infinito en la tecnología
En algunos lenguajes de programación, existe un valor especial llamado "infinito". Este valor puede aparecer cuando se realizan operaciones matemáticas que no tienen un resultado numérico normal, como dividir un número entre cero. Es una forma de que el programa indique que el resultado es "demasiado grande" o "sin límite".
El infinito en la filosofía
Desde la filosofía, el infinito se piensa como algo que no tiene ninguna restricción. Es algo ilimitado y sin fin. Si algo no tiene límites, significa que lo contiene todo y que no hay nada fuera de ello.
El infinito según Aristóteles
El filósofo griego Aristóteles pensaba que el infinito no existía "en la realidad" (en acto), sino solo "en potencia". Esto significa que algo es infinito porque siempre podemos añadirle más, pero nunca llegamos a un final. Por ejemplo, los números son infinitos en potencia porque siempre podemos añadir uno más. El espacio es infinito en potencia porque siempre podemos dividirlo en partes más pequeñas. El tiempo también es infinito en potencia porque sigue y sigue sin fin.
Aristóteles creía que lo finito era perfecto y lo infinito era imperfecto. Por eso, él no consideraba que Dios fuera infinito, ya que para él, la perfección estaba en lo limitado.
Historia del símbolo de infinito

El símbolo del infinito (∞) fue introducido en las matemáticas por el matemático inglés John Wallis en el año 1656, en su libro Arithmetica Infinitorum. Más tarde, en 1694, Jacob Bernoulli también lo usó.
Se cree que la forma de este símbolo podría venir de otras ideas antiguas, como la serpiente uróboros, que se muerde la cola y representa un ciclo sin fin. Otra idea es que se parece al analema solar, que es la figura que dibuja el Sol en el cielo si lo fotografiamos a la misma hora todos los días durante un año. Esta figura tiene forma de ocho, lo que simboliza un ciclo anual que se repite infinitamente.
El símbolo de infinito se puede encontrar en los teclados y sistemas informáticos con el código Unicode U+221E.
| Año | Acontecimiento |
|---|---|
| 350 a.C. | Aristóteles dice que el infinito real no existe. |
| 1639 | Gérard Desargues introduce la idea del infinito en la geometría. |
| 1655 | Se atribuye a John Wallis el primer uso del símbolo 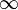 para el infinito. para el infinito. |
| 1874 | Georg Cantor describe diferentes tipos de infinito en la teoría de conjuntos. |
Galería de imágenes
-
El símbolo de infinito ∞ (Unicode U+221E), también llamado lemniscata, en diferentes tipos de letra.
Véase también
 En inglés: Infinity Facts for Kids
En inglés: Infinity Facts for Kids


