Media (matemáticas) para niños
En matemáticas y estadística, una media o promedio es un número que nos ayuda a entender el "centro" o el valor "típico" de un grupo de datos. Imagina que tienes varias calificaciones en un examen; el promedio te daría una idea de cómo te fue en general.
La media es un valor que se encuentra entre el número más pequeño y el más grande de un conjunto. Se calcula haciendo operaciones específicas con los números. Hay diferentes tipos de medias, como la media geométrica, la media ponderada y la media armónica. Sin embargo, cuando la gente habla de "la media" o "el promedio" en la vida diaria, casi siempre se refiere a la media aritmética.
Cada tipo de media busca resumir un grupo de datos, mostrando su tamaño y si son positivos o negativos. La elección de la media más útil depende de lo que estés midiendo y por qué.
Para un grupo completo de personas o cosas (llamado "población"), la media es el promedio de una característica específica de cada miembro. Por ejemplo, la altura promedio de una clase se calcula sumando las alturas de todos los estudiantes y dividiendo el resultado por el número total de estudiantes. Si solo tomas una parte de ese grupo (una "muestra"), la media de esa muestra puede ser un poco diferente de la media de toda la población, especialmente si la muestra es pequeña. Una regla importante en estadística dice que cuanto más grande sea tu muestra, más probable es que su media se parezca a la media de toda la población.
Contenido
Tipos de Medias y Cómo Calcularlas
Existen varias formas de calcular una media. Una característica que todas comparten es que la media siempre estará entre el valor más pequeño y el valor más grande del grupo de números. Además, si todos los números en un grupo son iguales, la media será ese mismo número.
Cómo calcular la Media Aritmética
La media aritmética es el tipo de promedio más común y el que usamos casi siempre. Para calcularla, simplemente sumas todos los números de tu grupo y luego divides esa suma por la cantidad total de números que tienes.
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \bar{x} = \frac{\text{Suma de todos los números}}{\text{Cantidad de números}}
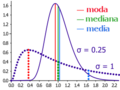
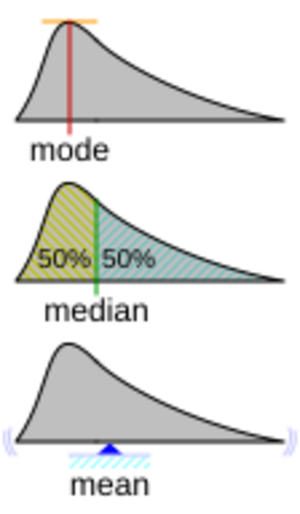
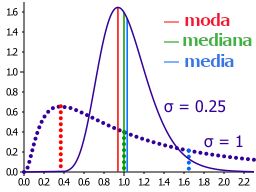
A veces, la media se confunde con la mediana o la moda. La media aritmética es el punto central de un conjunto de valores. Sin embargo, en grupos de datos donde los números no están distribuidos de manera uniforme (por ejemplo, si hay algunos valores muy altos o muy bajos que desequilibran el promedio), la media puede no ser igual a la mediana (el número del medio) o a la moda (el número que más se repite).
Por ejemplo, para calcular la media aritmética de los números 34, 27, 45, 55, 22 y 34 (hay seis números): Sumamos: 34 + 27 + 45 + 55 + 22 + 34 = 217 Dividimos por la cantidad de números (6): 217 / 6 ≈ 36.167 Así, la media aritmética es aproximadamente 36.167.
¿Cuándo usar la Media Aritmética Ponderada?
A veces, algunos datos son más importantes que otros. En esos casos, usamos la media ponderada. Imagina que en tu calificación final de una materia, el examen final vale más que una tarea. Para calcular tu promedio, le darías más "peso" o importancia a la calificación del examen final.
Para calcularla, multiplicas cada número por su "peso" (un valor que indica su importancia), sumas todos esos resultados y luego divides por la suma de todos los pesos.
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \bar{X}_w = \frac{\text{Suma de (cada número } \times \text{ su peso)}}{\text{Suma de todos los pesos}}
Cómo calcular la Media Geométrica
La media geométrica es útil cuando los números se relacionan por multiplicación, no por suma. Por ejemplo, se usa para calcular el crecimiento promedio de algo a lo largo del tiempo, como el crecimiento de una población o de una inversión.
Para calcularla, multiplicas todos los números de tu grupo y luego sacas la raíz enésima de ese producto, donde "n" es la cantidad de números.
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \bar{x} = \sqrt[n]{\text{Producto de todos los números}}
Por ejemplo, para los números 1, 2, 3, 4, 5 y 9 (seis valores): Multiplicamos: 1 × 2 × 3 × 4 × 5 × 9 = 1080 Sacamos la raíz sexta de 1080: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1080^{1/6} \approx 3.203 La media geométrica es aproximadamente 3.203.
Cómo calcular la Media Armónica
La media armónica es útil cuando los números representan tasas o velocidades. Por ejemplo, si calculas la velocidad promedio de un viaje donde recorres la misma distancia a diferentes velocidades.
Para calcularla, divides la cantidad total de números por la suma de los inversos de cada número (es decir, 1 dividido por cada número).
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \bar{x} = \frac{\text{Cantidad de números}}{\text{Suma de (1 / cada número)}}
Por ejemplo, para los números 34, 27, 45, 55, 22 y 34: Sumamos sus inversos: (1/34) + (1/27) + (1/45) + (1/55) + (1/22) + (1/34) ≈ 0.1817 Dividimos la cantidad de números (6) por esa suma: 6 / 0.1817 ≈ 33.018 La media armónica es aproximadamente 33.018.
La Media en la Vida Real
La Media en la Escuela
El promedio se usa mucho en la escuela para evaluar a los estudiantes. En muchos países, las calificaciones se dan con números. Por ejemplo:
- En España: de 0 a 10.
- En Francia, Túnez, Argelia y Marruecos: de 0 a 10 o de 0 a 20.
- En Suiza: del 1 al 6.
- En Alemania: de 6 a 1.
- En Canadá: de 0 a 100.
- En Dinamarca: de -3 a 12.
Podemos calcular el promedio de las calificaciones de una clase en una materia, o el promedio de las calificaciones de un estudiante en varias materias. Estos promedios nos dan información útil:
- El promedio de la clase puede mostrar el nivel general de los estudiantes en una materia.
- El promedio de las calificaciones de un estudiante en una materia ayuda a ver su rendimiento general, compensando si tuvo un mal día en un examen con un buen día en otro.
- El promedio de las calificaciones de un estudiante en varias materias ayuda a ver su rendimiento general en todas las asignaturas, donde sus puntos fuertes pueden compensar sus puntos débiles. Si algunas materias son más importantes, se usan medias ponderadas.
En estos casos, el promedio ayuda a "suavizar" los resultados y dar una visión más equilibrada.
La Media en Estadística
En estadística, la media es el valor que todos los individuos de un grupo (población o muestra) tendrían si su total no cambiara. Es una forma de saber dónde se "ubican" los datos.
Si el "total" de un grupo de datos se calcula sumando sus valores (que es lo más común), entonces la media que usamos es la media aritmética. Pero si el "total" se calcula de otra manera (por ejemplo, multiplicando los valores), entonces se usa otro tipo de media, como la media geométrica.
La media solo se puede calcular para números. No podemos calcular la media de cosas que no son números, como colores o tipos de animales.
La Media en Geometría
En geometría, el baricentro (o centro de masa) de un grupo de puntos se calcula usando la media aritmética ponderada de las coordenadas de esos puntos. Es como encontrar el punto de equilibrio de una figura.
La Media en Probabilidades
En probabilidad, la media de una muestra de números aleatorios es simplemente la media aritmética de esos números. Esta media nos ayuda a estimar el valor esperado de una variable aleatoria, que es el promedio que esperaríamos obtener si repitiéramos un experimento muchas veces.
La Media en Física
En física, las reglas que explican cómo se conservan ciertas cantidades (como la energía) nos llevan a usar diferentes tipos de promedios.
Por ejemplo, la capacidad promedio de varios condensadores conectados en serie se calcula con la media armónica de sus capacidades. De manera similar, la resistencia promedio de varios cables eléctricos conectados en paralelo también usa la media armónica.
La energía cinética (la energía del movimiento) depende del cuadrado de la velocidad. Por eso, la velocidad promedio de un grupo de partículas que se mueven por el calor se calcula con la media cuadrática de sus velocidades individuales.
Galería de imágenes
-
Visualisation mode median mean.svg?lang=es
Visualización geométrica de la moda, la mediana y de la media de una función arbitraria de densidad de probabilidad.
-
Comparación de la media aritmética (azul), la mediana (verde) y la moda (rojo) de dos distribuciones log-normal con diferente asimetría.
Véase también
En inglés: Mean Facts for Kids
