Distribución de Maxwell-Boltzmann para niños
La distribución de Boltzmann o distribución de Maxwell-Boltzmann es una forma especial de entender cómo se mueven las partículas en un gas. Imagina que tienes un montón de moléculas de gas volando por todas partes. Esta distribución nos ayuda a saber qué tan rápido se mueven esas moléculas a una temperatura específica.
Fue creada por dos científicos muy importantes: J. C. Maxwell y L. Boltzmann. Ellos querían responder a una pregunta clave: "¿Cómo se distribuyen las velocidades de las moléculas en un gas cuando tiene una temperatura determinada?".
En términos sencillos, la distribución de Maxwell-Boltzmann nos muestra que no todas las moléculas de un gas se mueven a la misma velocidad. Algunas van más rápido, otras más lento, y la mayoría se mueve a una velocidad intermedia. La distribución de Boltzmann, por otro lado, se usa más para hablar de la energía de esas partículas. Ambas están relacionadas, pero se enfocan en aspectos ligeramente diferentes.
Contenido
¿Cómo se distribuyen las velocidades en un gas?
Para entender cómo se distribuyen las velocidades de las moléculas en un gas, los científicos usan una fórmula matemática. Esta fórmula nos ayuda a calcular la probabilidad de que una molécula tenga una velocidad específica.
Piensa en la velocidad de una molécula como si tuviera tres partes: una velocidad en la dirección X, otra en la dirección Y y otra en la dirección Z. La velocidad total de la molécula es como la "suma" de estas tres partes.
La fórmula que describe esta distribución de velocidades es:
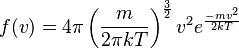
En esta fórmula:
- m es la masa de una sola partícula o molécula.
- k es la constante de Boltzmann, un número que ayuda a relacionar la energía de las partículas con la temperatura.
- T es la temperatura del gas, medida en una escala especial llamada Kelvin.
- v es la velocidad de la partícula.
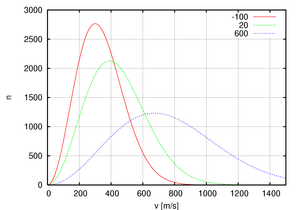
Esta fórmula nos dice que, a medida que la temperatura aumenta, las moléculas tienden a moverse más rápido. Por eso, en el gráfico, la curva se estira hacia velocidades más altas cuando la temperatura sube.
¿Cuáles son las velocidades importantes en un gas?
Cuando estudiamos la distribución de velocidades, hay algunas velocidades "típicas" que nos interesan:
La velocidad más común (velocidad más probable)
Esta es la velocidad a la que se mueven la mayor cantidad de moléculas en el gas. Es como la velocidad "favorita" de las partículas. Se calcula con la siguiente fórmula:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): v_p = \sqrt { \frac{2kT}{m} }
Por ejemplo, para el gas nitrógeno (N2) a una temperatura ambiente de 300 Kelvin (que es como 27 °C), la velocidad más común es de aproximadamente 422 metros por segundo. ¡Eso es muy rápido!
La velocidad promedio (velocidad media)
Esta es la velocidad que obtendrías si sumaras las velocidades de todas las moléculas y luego las dividieras por el número total de moléculas. Es un promedio de todas las velocidades.
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \langle v \rangle = \sqrt { \frac{8kT}{\pi m}}
La velocidad cuadrática media
Esta velocidad es un poco más compleja, pero es muy útil en física. Se calcula tomando el promedio de los cuadrados de las velocidades de todas las moléculas y luego sacando la raíz cuadrada de ese resultado. Nos da una idea de la energía cinética promedio de las moléculas.
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sqrt{\langle v^2 \rangle} = \sqrt { \frac{3kT}{m}}
Estas tres velocidades están relacionadas entre sí. Siempre se cumple que la velocidad más probable es un poco menor que la velocidad media, y la velocidad media es un poco menor que la velocidad cuadrática media.
Galería de imágenes
-
Distribución de velocidades de un conjunto de 1.000.000 moléculas de oxígeno a tres temperaturas diferentes: -100 °C; 20 °C y 600 °C. Cuando la temperatura es más alta, las moléculas se mueven más rápido.
Véase también
En inglés: 