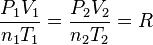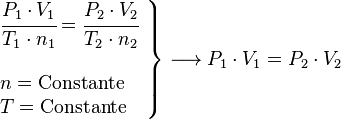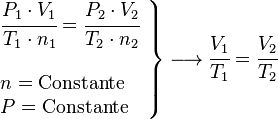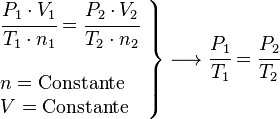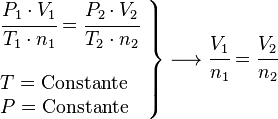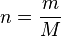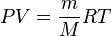robot de la enciclopedia para niños

Ley de los gases ideales para niños

Enciclopedia para niños

La ley de los gases ideales es una fórmula muy importante en la física y la química. Nos ayuda a entender cómo se comportan los gases en diferentes situaciones. Esta ley describe un "gas ideal", que es como un gas perfecto imaginario. En este gas, las partículas son muy pequeñas, no se atraen ni se repelen entre sí, y cuando chocan, lo hacen de forma elástica, como pelotas de goma que rebotan sin perder energía.

La energía de movimiento de las partículas en un gas ideal está directamente relacionada con su temperatura. Los gases que más se parecen a este gas ideal son los que tienen átomos solos (como el helio) cuando la presión es baja y la temperatura es alta.

Una idea clave de esta ley es que si mantienes la temperatura de un gas constante, su presión y su volumen se relacionan de forma inversa. Esto significa que si la presión aumenta, el volumen disminuye, y si la presión baja, el volumen aumenta.

Matemáticamente, esto se puede escribir así:

PV = k
Símbolo Nombre
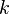k Una constante (un número fijo) si la temperatura y la cantidad de gas no cambian.

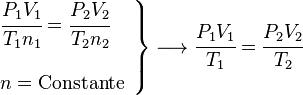
Si tienes un gas en dos situaciones diferentes (1 y 2), pero la cantidad de gas y la temperatura son las mismas, se cumple esta relación:

P_1V_1 = P_2V_2 \,

Las primeras ideas sobre las leyes de los gases surgieron a finales del siglo XVII. Científicos como August Krönig en 1856 y Rudolf Clausius en 1857 trabajaron en ellas. Más tarde, en 1874, Dmitri Mendeleev introdujo la constante universal de los gases, que es un número que funciona para todos los gases ideales.

Con el tiempo, los científicos se dieron cuenta de que la presión, el volumen y la temperatura de un gas en un recipiente cerrado se relacionaban de una manera que servía para todos los gases. Esto es porque las moléculas de los gases, al estar separadas, se comportan de forma similar. Hoy en día, la ecuación del gas ideal se explica con la teoría cinética de los gases. Las leyes más antiguas se consideran casos especiales de esta ecuación, donde una o más de las variables se mantienen fijas.

La ley de los gases ideales fue propuesta por primera vez por Émile Clapeyron en 1834, combinando las ideas de la ley de Boyle y la ley de Charles.

La Ecuación Principal de los Gases Ideales

El "estado" de un gas se define por su presión, volumen y temperatura. La ecuación moderna de los gases ideales conecta estas tres cosas con la cantidad de gas. Es importante saber que la temperatura que se usa en esta ecuación debe ser una temperatura absoluta, como los kelvin (K) en el sistema internacional.

La Fórmula Más Común

La ecuación que describe la relación entre la presión, el volumen, la temperatura y la cantidad de gas (medida en moles) es:

PV = nRT
Símbolo Nombre
P Presión absoluta (la fuerza que el gas ejerce por unidad de área)
V Volumen (el espacio que ocupa el gas)
n Moles de gas (la cantidad de gas)
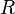R Constante universal de los gases ideales (un número fijo para todos los gases ideales)
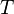T Temperatura absoluta (en Kelvin)

¿Qué dice la Teoría Cinética Molecular?

Esta teoría, desarrollada por Ludwig Boltzmann y James Clerk Maxwell, nos ayuda a entender cómo se comporta un gas ideal a nivel de sus partículas (átomos o moléculas):

  • Un gas ideal está hecho de muchísimas partículas muy pequeñas.
  • Estas partículas se mueven muy rápido, en línea recta y de forma desordenada.
  • El gas ejerce presión porque sus partículas chocan continuamente contra las paredes del recipiente.
  • Los choques entre las partículas son "elásticos", lo que significa que no pierden energía al chocar.
  • No se consideran las fuerzas de atracción o repulsión entre las partículas.
  • La energía de movimiento promedio de una partícula es directamente proporcional a la temperatura absoluta del gas.

Gases Reales vs. Gases Ideales

La ecuación de los gases ideales funciona muy bien para muchos gases en condiciones normales. Sin embargo, los gases "reales" no son exactamente como los gases ideales. Las partículas de los gases reales sí tienen un tamaño y sí se atraen o repelen un poco entre sí.

Para describir mejor a los gases reales, existe una ecuación más compleja llamada ecuación de Van der Waals. Esta ecuación añade correcciones a la fórmula del gas ideal para tener en cuenta el tamaño de las partículas y las fuerzas entre ellas.

Ecuación General de los Gases Ideales

Si partimos de la ecuación PV = nRT, podemos reordenarla para ver que 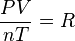\frac{PV }{nT} = R. Como R es una constante, esto significa que para dos estados diferentes (1 y 2) del mismo gas, se cumple:

\frac{P_1 V_1 }{n_1 T_1} = \frac{P_2 V_2 }{n_2 T_2} = R

Si la cantidad de gas (n) no cambia, la ecuación se simplifica a:

\left . \begin{array}{l} \cfrac{P_1 V_1}{T_1 n_1}= \cfrac{P_2 V_2}{T_2 n_2} \\ \; \\ n = \rm{Constante} \end{array} \right \} \longrightarrow \cfrac{P_1 V_1}{T_1} = \cfrac{P_2 V_2}{T_2}

Esto nos dice que el producto de la presión y el volumen es directamente proporcional a la temperatura del gas.

Procesos Gaseosos Particulares

Cuando una o más de las variables (cantidad de gas, presión, volumen, temperatura) se mantienen constantes, la ley de los gases ideales se simplifica y da lugar a otras leyes más específicas:

Ley de Boyle-Mariotte (Temperatura Constante)

También se le llama proceso isotérmico. Esta ley dice que, si la temperatura y la cantidad de gas no cambian, la presión de un gas es inversamente proporcional a su volumen. Es decir, si la presión sube, el volumen baja.

\left . \begin{array}{l} \cfrac{P_1 \cdot V_1}{T_1 \cdot n_1}=\cfrac{P_2 \cdot V_2}{T_2 \cdot n_2} \\ \; \\ n = \rm{Constante} \\ T = \rm{Constante} \end{array} \right \} \longrightarrow P_1 \cdot V_1 = P_2 \cdot V_2

Ley de Charles (Presión Constante)

Esta ley, parte de los trabajos de Jacques Charles y Louis Gay-Lussac, describe un proceso isobárico (presión constante). Dice que, si la presión y la cantidad de gas no cambian, el volumen de un gas es directamente proporcional a su temperatura. Si la temperatura sube, el volumen también.

\left . \begin{array}{l} \cfrac{P_1 \cdot V_1}{T_1 \cdot n_1}=\cfrac{P_2 \cdot V_2}{T_2 \cdot n_2} \\ \; \\ n = \rm{Constante} \\ P = \rm{Constante} \end{array} \right \} \longrightarrow \cfrac{V_1}{T_1}= \cfrac{V_2}{T_2}

Ley de Gay-Lussac (Volumen Constante)

También se le llama proceso isocórico (volumen constante). Esta ley establece que, si el volumen y la cantidad de gas no cambian, la presión de un gas es directamente proporcional a su temperatura. Si la temperatura sube, la presión también.

\left . \begin{array}{l} \cfrac{P_1 \cdot V_1}{T_1 \cdot n_1}=\cfrac{P_2 \cdot V_2}{T_2 \cdot n_2} \\ \; \\ n = \rm{Constante} \\ V = \rm{Constante} \end{array} \right \} \longrightarrow \cfrac{P_1}{T_1}= \cfrac{P_2}{T_2}

Principio de Avogadro (Presión y Temperatura Constantes)

Este principio fue propuesto por Amedeo Avogadro en 1811. Dice que, si la presión y la temperatura se mantienen constantes, el volumen de cualquier gas es directamente proporcional al número de moles (la cantidad) de gas presente.

\left . \begin{array}{l} \cfrac{P_1 \cdot V_1}{T_1 \cdot n_1}=\cfrac{P_2 \cdot V_2}{T_2 \cdot n_2} \\ \; \\ T = \rm{Constante} \\ P = \rm{Constante} \end{array} \right \} \longrightarrow \cfrac{V_1}{n_1}=\cfrac{V_2}{n_2}

Una forma sencilla de entenderlo es que un mol de cualquier gas ideal siempre ocupa el mismo volumen si la temperatura y la presión son las mismas.

Otras Formas de la Ecuación

A veces, en lugar de usar el número de moles (n), es útil usar la masa (m) del gas. Sabemos que el número de moles se puede calcular como la masa (m) dividida por la masa molar (M) del gas:

n = {\frac{m}{M}}
Símbolo Nombre
n Número de moles
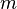m Masa del gas
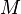M Masa molar del gas

Si sustituimos "n" en la ecuación principal, obtenemos:

PV = \frac{m}{M}RT

Esta forma es muy útil porque relaciona la presión, la densidad (que es la masa dividida por el volumen, ρ = m/V) y la temperatura en una sola fórmula, sin importar la cantidad total de gas.

Galería de imágenes

  • Several isotherms of an ideal gas on a P, T, V-diagram

    Isotermas de un gas ideal en un gráfico de Presión, Temperatura y Volumen.

Véase también

Kids robot.svg En inglés: Ideal gas law Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Ley_de_los_gases_ideales&oldid=5063113»
kids search engine
Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:
Ley de los gases ideales para Niños. Enciclopedia Kiddle.