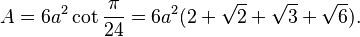Icositetrágono para niños
Datos para niños Icositetrágono |
||
|---|---|---|
 Un icositetrágono regular
|
||
| Características | ||
| Tipo | Polígono regular | |
| Lados | 24 | |
| Vértices | 24 | |
| Grupo de simetría | 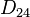 , orden 2x24 , orden 2x24 |
|
| Símbolo de Schläfli | {24}, t{12}, tt{6}, ttt{3} (icositetrágono regular) | |
| Diagrama de Coxeter-Dynkin | ||
| Polígono dual | Autodual | |
| Área | 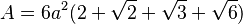 (lado  ) ) |
|
| Ángulo interior | 165° | |
| Propiedades | ||
| Convexo, isogonal, cíclico | ||
En geometría, un icositetrágono (también llamado icosikaitetrágono o 24-gono) es una figura plana que tiene veinticuatro lados y veinticuatro vértices. La suma de todos los ángulos que están dentro de un icositetrágono siempre es de 3960 grados.
Contenido
¿Qué es un Icositetrágono Regular?
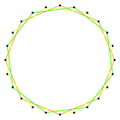
Un icositetrágono regular es un tipo especial de icositetrágono donde todos sus lados miden lo mismo y todos sus ángulos interiores son iguales. Se representa con el símbolo de Schläfli {24}. Este símbolo es una forma abreviada de describir polígonos y otras figuras geométricas.
Cómo se forma un Icositetrágono Regular
Un icositetrágono regular se puede crear de varias maneras a partir de otros polígonos:
- Se puede formar al "truncar" un dodecágono (una figura de 12 lados). Truncar significa cortar las esquinas de una figura.
- También se puede obtener truncando un hexágono (6 lados) dos veces.
- O incluso truncando un triángulo (3 lados) tres veces.
Medidas de los Ángulos y el Área
Cada ángulo interior de un icositetrágono regular mide 165 grados. Esto significa que el ángulo exterior (el que se forma al extender uno de sus lados) mide 15 grados.
Para calcular el área de un icositetrágono regular, si conoces la longitud de uno de sus lados (llamémosla a), puedes usar la siguiente fórmula:
El icositetrágono fue una de las figuras que el famoso matemático Arquímedes usó para calcular una aproximación del número π. Él lo hizo usando polígonos regulares con cada vez más lados, como el hexágono (6 lados), el dodecágono (12 lados), el tetracontaoctágono (48 lados) y el eneacontahexágono (96 lados).
¿Cómo se construye un Icositetrágono?
Un icositetrágono regular se puede construir usando herramientas de geometría. Esto es posible porque el número 24 se puede descomponer en 23 × 3. Se puede construir a partir de un dodecágono regular dividiendo sus lados por la mitad.
Simetría de un Icositetrágono Regular
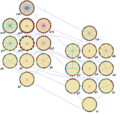
Un icositetrágono regular tiene una simetría muy especial llamada Dih24. Esto significa que si lo giras o lo volteas de ciertas maneras, se verá exactamente igual. En total, tiene 48 formas de simetría diferentes.
Existen varios tipos de simetrías para esta figura:
- Simetrías diédricas: Son como si pudieras doblar el polígono por una línea y ambas mitades coincidieran. Algunas líneas de simetría pasan por los vértices y otras por el centro de los lados.
- Simetrías cíclicas: Son simetrías de giro, donde el polígono se ve igual después de girarlo un cierto ángulo.
¿Cómo se puede dividir un Icositetrágono?
 regular |
 Isotoxal |
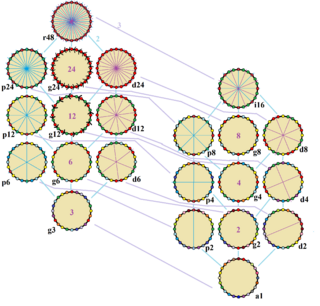
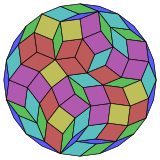
El matemático Harold Scott MacDonald Coxeter descubrió que ciertos polígonos, llamados zonágonos (que tienen un número par de lados y sus lados opuestos son paralelos), se pueden dividir en paralelogramos. Un icositetrágono regular es un zonágono.
Un icositetrágono regular se puede dividir en 66 rombos (que son un tipo de paralelogramo). De estos, 6 son cuadrados y los otros 60 se agrupan en 5 conjuntos de 12 rombos.
 |
 |
 |
 |
Polígonos relacionados con el Icositetrágono
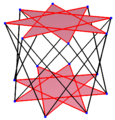
Un icositetragrama es una figura de estrella que también tiene 24 "puntas" o lados. Hay diferentes tipos de icositetragramas regulares, que se nombran con símbolos como {24/5}, {24/7} y {24/11}. También hay otras figuras de estrellas que comparten los mismos puntos (vértices) que un icositetrágono.
También existen icositetragramas isogonales. Estos se forman al "truncar" más profundamente un dodecágono regular {12} o un dodecagrama {12/5}.
| Truncamientos isogonales de dodecágono y dodecagrama regulares | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Cuasiregular | Isogonal | Cuasiregular | |||||||||
 t{12}={24} |
 |
 |
 |
 |
 |
 t{12/11}={24/11} |
|||||
 t{12/5}={24/5} |
 |
 |
 |
 |
 |
 t{12/7}={24/7} |
|||||
Icositetrágono Oblicuo
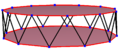
Un icositetrágono oblicuo es un polígono alabeado. Esto significa que tiene 24 vértices y lados, pero no todos se encuentran en el mismo plano (como si estuvieran en 3D y no en una hoja de papel). Su interior no está definido de la misma manera que un polígono plano.
Un tipo especial es el icositetrágono en zig-zag oblicuo. Sus vértices se alternan entre dos planos que son paralelos entre sí.
Un icositetrágono oblicuo regular tiene todos sus lados de la misma longitud y es una figura isogonal. En el espacio tridimensional, se ve como un icositetrágono en zig-zag. Puedes encontrarlo en las aristas de un antiprisma dodecagonal, que es una figura geométrica con dos bases de 12 lados y caras triangulares que las conectan.
Polígonos de Petrie
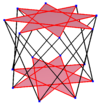
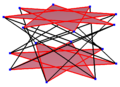
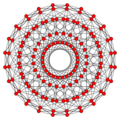
El icositetrágono regular es un polígono de Petrie para muchas figuras geométricas de dimensiones superiores, llamadas politopos. Un polígono de Petrie es una secuencia de aristas de un politopo que forma un camino cerrado y no se cruza.
| 2F4 | ||
|---|---|---|
 24-celdas bitruncado |
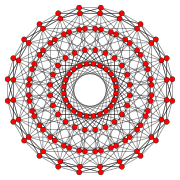 24-celdas runcinado |
 24-celdas omnitruncado |
| E8 | ||
|---|---|---|
 421 |
 241 |
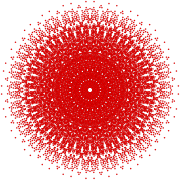 142 |
Galería de imágenes
Véase también
 En inglés: Regular polygon Facts for Kids
En inglés: Regular polygon Facts for Kids