Horizonte para niños

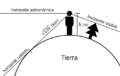
El horizonte es la línea que parece separar el cielo y la Tierra. Para nosotros, que estamos en la superficie, esta línea se ve como un círculo a nuestro alrededor.

En ciencia, el horizonte también se puede definir de otras maneras. Por ejemplo, el horizonte astronómico es un plano imaginario que pasa por el centro de la Tierra y es perpendicular a una línea que va desde el centro de la Tierra hasta justo encima de nuestra cabeza. Aunque parezca complicado, para nosotros en la superficie, este plano es casi el mismo que un plano que pasa por nuestros ojos y es paralelo al suelo.

Existen diferentes tipos de horizontes, dependiendo de cómo los observemos:

• Horizonte aparente: Es el plano ideal que toca la superficie de la Tierra justo donde estamos.
• Horizonte sensible o horizonte real: Este es el horizonte que vemos en la vida diaria, afectado por montañas, edificios o árboles.
• Horizonte geométrico: Es una superficie con forma de cono que tiene su punta en el observador y toca la superficie de la Tierra.
• Horizonte físico o horizonte óptico: Este horizonte se ve afectado por cómo la luz se dobla en la atmósfera (refracción atmosférica), lo que nos permite ver un poco más allá del horizonte real.
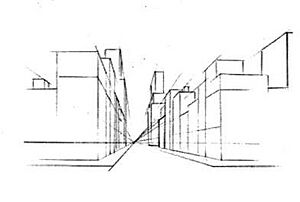
• Línea del horizonte: En el dibujo y la perspectiva, es la línea donde el suelo parece terminar en el plano de la imagen. Cuando estamos al nivel del mar, esta línea es muy parecida al horizonte aparente. Es muy importante para dibujar, porque es el punto donde todas las líneas horizontales parecen unirse.

Casi todos los tipos de horizontes que vemos (excepto el astronómico y el aparente) son "ópticos", porque la luz se dobla al pasar por el aire.

El horizonte es muy importante para la navegación y para ubicar objetos en el cielo, como estrellas o planetas. Cuando medimos la altura de una estrella sobre el horizonte, primero lo hacemos con el horizonte que vemos (aparente) y luego hacemos ajustes por cómo se dobla la luz en el aire y por la distancia a la Tierra.

La forma en que la luz se dobla en la atmósfera hace que veamos el Sol un poco más alto de lo que realmente está. Por eso, cuando el Sol parece tocar el mar al atardecer, en realidad ya está un poco por debajo de nuestro horizonte real.

¿De dónde viene la palabra "horizonte"?

Ocaso sobre el horizonte en Gran Canaria.

La palabra "horizonte" viene del griego antiguo horízōn kýklos, que significa "círculo que limita" o "círculo que separa". La palabra horízōn viene del verbo griego horízō, que significa "dividir" o "separar", y esta a su vez viene de hóros, que significa "límite".

¿Cómo se ve el horizonte?

Los dibujos en perspectiva tienen una línea análoga al horizonte donde las líneas paralelas convergen en un punto de fuga.

Saber la distancia al horizonte visible fue muy importante en el pasado para la supervivencia y la navegación, especialmente en el mar. Esto ayudaba a saber hasta dónde se podía ver y comunicarse. Aunque hoy tenemos la radio y el telégrafo, el horizonte sigue siendo útil. Por ejemplo, los pilotos de aviones lo usan para controlar la aeronave y no perder la orientación.

Cuando dibujamos en perspectiva, a menudo no consideramos la curvatura de la Tierra. En ese caso, el horizonte es una línea teórica donde todas las líneas paralelas parecen unirse a medida que se alejan del observador. Para alguien cerca del nivel del mar, la diferencia entre este horizonte de dibujo (que asume una Tierra plana) y el horizonte real (que asume una Tierra redonda) es casi imposible de notar. Sin embargo, si estás en una montaña alta, el horizonte real se verá un poco más abajo que una línea perfectamente horizontal.

En la astronomía, el horizonte es un plano horizontal que pasa por los ojos del observador. Es la base para ubicar objetos en el cielo, donde los objetos que están en este plano tienen una altura de cero grados.

Distancia al horizonte

¿Cómo se calcula la distancia al horizonte?

Teorema de la tangente-secante.

Si imaginamos que la Tierra es una esfera perfecta y no consideramos cómo la atmósfera dobla la luz, podemos calcular la distancia al horizonte de forma sencilla.

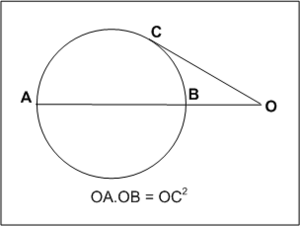
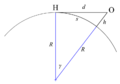
Podemos usar un teorema de geometría llamado el teorema de la tangente-secante. Si llamamos d a la distancia al horizonte, D al diámetro de la Tierra y h a la altura del observador sobre el nivel del mar, la fórmula es:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): d = \sqrt{h(D+h)}

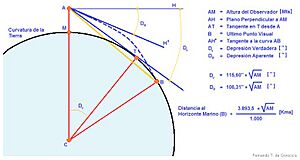
También podemos usar el teorema de Pitágoras. Imagina un triángulo rectángulo donde la línea de visión al horizonte es un lado, el radio de la Tierra es otro lado, y la hipotenusa es el radio de la Tierra más tu altura. La fórmula sería:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): d^2+R^2 = (R+h)^2

Si despejamos d, obtenemos:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): d = \sqrt{2 R h + h^2}

Donde R es el radio de la Tierra (aproximadamente 6378,1 kilómetros).

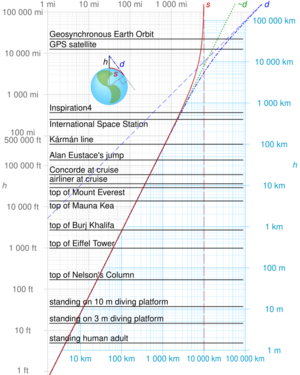
Por ejemplo, si un satélite está a 2000 kilómetros de altura, la distancia a su horizonte es de unos 5430 kilómetros.

Una forma más sencilla de calcularlo

Representación logarítmica de distancias del horizonte verdadero en la Tierra para una altura h dada, donde s es la distancia a lo largo de la superficie de la Tierra, d es la distancia en línea recta y ~d es la distancia aproximada en línea recta suponiendo que h es mucho menor que el radio de la Tierra, 6371 km.

Si el observador está cerca de la superficie de la Tierra (por ejemplo, en una montaña o en un avión), podemos usar una fórmula más sencilla. La fórmula se convierte en:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): d \approx \sqrt{2Rh}

Si usas kilómetros para la distancia d y el radio R, y metros para la altura h, la distancia al horizonte es aproximadamente:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): d \approx 3.570\sqrt{h}

Esto significa que si estás a 1.5 metros del suelo, el horizonte está a unos 4.4 kilómetros. Si estás en un avión a 10,000 metros de altura, el horizonte está a casi 360 kilómetros. Y desde la Estación Espacial Internacional a 420 kilómetros de altura, el horizonte está a más de 2300 kilómetros.

Estas fórmulas son muy precisas para alturas que son mucho menores que el radio de la Tierra.

Distancia máxima para ver entre dos lugares elevados

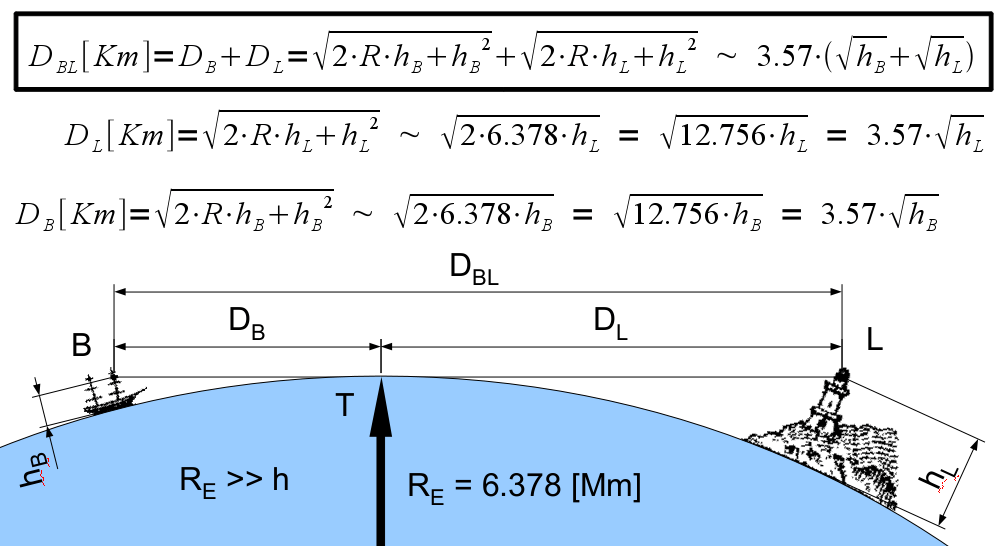
Si tienes dos lugares elevados, como un barco y un faro, puedes calcular la distancia máxima a la que se pueden ver el uno al otro. Esta distancia es la suma de la distancia al horizonte desde cada uno de ellos.

Por ejemplo, si una persona en un barco está a una altura hB sobre el mar y otra persona en un faro está a una altura hL, la distancia visible entre ellos es:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): D_B + D_L < 3.57\,(\sqrt{h_\mathrm{B}} + \sqrt{h_\mathrm{L}})

Donde las distancias están en kilómetros y las alturas en metros.

Imagina que un navegante en un barco está a 6 metros sobre el mar y ve la parte superior de un faro de 20 metros de altura. Como solo ve la parte de arriba, sabe que la parte de abajo está oculta por la curvatura de la Tierra. Puede calcular la distancia al faro:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): D_{BL}=3.572\,(\sqrt{6} + \sqrt{20})

Esto da aproximadamente 25 kilómetros.

De manera similar, puedes calcular cuánto de un objeto distante es visible sobre el horizonte. Si estás a 10 metros sobre el mar y ves un barco a 20 kilómetros de distancia, tu horizonte está a unos 11.3 kilómetros. El barco está 8.7 kilómetros más allá de tu horizonte. La altura del barco que apenas puedes ver se calcula así:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): h\approx\left(\frac{8.7}{3.57}\right)^2

Esto da casi 6 metros. Significa que solo puedes ver la parte del barco que está a más de 6 metros sobre el agua. La parte de abajo está oculta por la curvatura de la Tierra. A esto se le llama que el barco está "casco abajo".

Efecto de la refracción atmosférica

Cálculo de la Depresión del Horizonte. Depresión Verdadera y Aparente que se mide en el horizonte marino.

Si la Tierra no tuviera atmósfera, la luz viajaría en línea recta y los cálculos anteriores serían exactos. Pero la Tierra tiene aire, y la densidad del aire cambia con la temperatura y la presión. Esto hace que la luz se doble (se refracte). Generalmente, el aire es más denso cerca de la superficie, lo que hace que la luz se curve hacia abajo. Por eso, la distancia real al horizonte es un poco mayor de lo que calculamos con las fórmulas geométricas. En condiciones normales, esta diferencia es de aproximadamente un 8%.

Cuando las condiciones atmosféricas son inusuales, esta aproximación puede no ser correcta. Por ejemplo, si el aire caliente está sobre agua fría, la luz puede seguir la superficie de la Tierra por cientos de kilómetros. En los desiertos, el aire caliente cerca del suelo puede hacer que la luz se curve hacia arriba, creando espejismos y haciendo que el concepto de horizonte sea confuso.

Para calcular la distancia al horizonte considerando la refracción, se usa un "radio efectivo" de la Tierra que es un poco más grande que el real. Por ejemplo, en topografía, se suele usar un radio de 7681 km o 7433 km en lugar de los 6371 km reales.

Una forma sencilla de calcular la distancia al horizonte con refracción es usando un radio de la Tierra multiplicado por 7/6. La fórmula sería:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): d=\sqrt{2 R^\prime h}

Donde R' es el radio ajustado. Si d está en kilómetros y h en metros, la fórmula es:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): d \approx 3.86 \sqrt{h}

Curvatura del horizonte

La curvatura del horizonte se ve fácilmente en esta fotografía de 2008, tomada desde un transbordador espacial a una altitud de 226 km (140 mi).

Desde un punto alto sobre la Tierra, el horizonte no se ve como una línea recta, sino ligeramente curvo, como un arco. Cuanto más alto estés, más notoria será esta curvatura. Por ejemplo, desde un avión a 10 kilómetros de altura, la curvatura es pequeña, pero se puede calcular. Sin embargo, la curvatura que vemos es menor de lo que debería ser debido a cómo la luz se dobla en la atmósfera y a las nubes altas que pueden ocultar parte del horizonte.

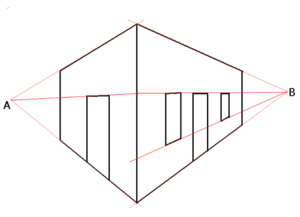
Punto de fuga

Dos puntos en el horizonte están en las intersecciones de las líneas que extienden los segmentos que representan los bordes del edificio en primer plano. La línea del horizonte coincide aquí con la línea en la parte superior de las puertas y ventanas.

En el dibujo en perspectiva, el horizonte es una parte clave. Si el dibujo está en una superficie vertical al suelo, el horizonte es una línea horizontal que pasa por un punto especial llamado "punto de fuga". Este punto de fuga es donde todas las líneas que son perpendiculares a la imagen parecen unirse. Si hay otro punto en el horizonte, también es un punto de fuga para todas las líneas paralelas a la línea que conecta el ojo del observador con ese punto.

La idea de que las líneas paralelas se encuentran en la distancia en el horizonte ayudó a desarrollar una rama de las matemáticas llamada geometría proyectiva.

Galería de imágenes

• 

  Representación artística del horizonte por computador.

• 

  Diagrama de tres tipos de horizontes.

• 

  Una vista del horizonte desde la costa de España. En el que se puede ver la curvatura de la Tierra. Los tanques se encuentran en un muelle de Port de Sagunt (Saggas) a una distancia de unos 20 kilómetros de Valencia.

• 

  Distancia geométrica al horizonte mediante el teorema de Pitágoras.

• 
• 

Véase también

En inglés: Horizon Facts for Kids

• Cenit
• Nadir
• Acimut
• Tierra esférica