Representación logarítmica para niños
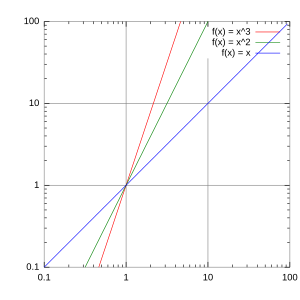
Una representación logarítmica es una forma especial de dibujar gráficas donde los números en los ejes no están espaciados de manera uniforme. En lugar de eso, se usa una escala logarítmica. Esto significa que la distancia entre 1 y 10 es la misma que entre 10 y 100, o entre 100 y 1000. Es como si cada paso multiplicara por 10 en lugar de sumar una cantidad fija.
Cuando se hacen estas gráficas a mano, se usa un papel especial llamado papel logarítmico. Este papel ya tiene las marcas listas para que sea más fácil dibujar. Generalmente, se usan logaritmos de base 10, que son los más comunes.
Contenido
¿Para qué se usan las Gráficas Logarítmicas?
Las representaciones logarítmicas son muy útiles cuando los datos que queremos mostrar cambian mucho, cubriendo un rango muy grande de números. Por ejemplo, si tienes números que van desde 1 hasta 1.000.000, una gráfica normal sería muy difícil de leer. Con una escala logarítmica, todos esos números caben bien.
También son muy usadas en ciencia e ingeniería para mostrar relaciones donde una cantidad crece o decrece muy rápido, como las funciones potenciales (por ejemplo, y=a·xn). Lo interesante es que, si tus datos siguen una relación de este tipo, al graficarlos en una escala logarítmica, ¡se ven como una línea recta! Esto hace que sea mucho más fácil entender la relación entre los datos.
Un Ejemplo con los Planetas
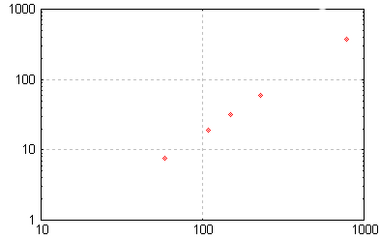
Un buen ejemplo de dónde se usan las gráficas logarítmicas es para mostrar los datos de los planetas. Vamos a ver cómo el tiempo que tarda un planeta en dar la vuelta al Sol (su periodo de revolución) se relaciona con la distancia promedio al Sol (su semieje mayor). Esto sigue las leyes de Kepler.
Aquí tienes una tabla con algunos datos:
| Planeta | Semieje mayor en 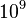 m m |
Periodo de revolución en 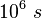 |
| Mercurio | 57,9 | 7,58 |
| Venus | 108,2 | 19,36 |
| Tierra | 149,6 | 31,47 |
| Marte | 227,9 | 59,19 |
| Júpiter | 778,3 | 373,32 |
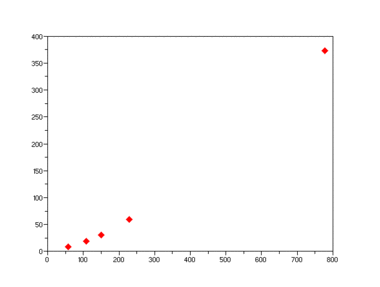
Si intentáramos dibujar estos datos en una gráfica normal, los primeros planetas (Mercurio, Venus, Tierra, Marte) estarían muy juntos, y Júpiter estaría muy lejos. Sería difícil ver la relación. Pero en una gráfica logarítmica, ¡se ve una línea recta! Esto nos ayuda a entender mejor cómo se relacionan estas dos cantidades.
| Representación logarítmica | Representación lineal |
|---|---|
| Esta gráfica logarítmica muestra el periodo de revolución de los planetas frente a su semieje mayor. Los puntos forman una línea recta, lo que facilita ver la relación. | La misma información en una gráfica normal (cartesiana) haría que los primeros puntos se amontonaran y el último punto quedara muy lejos, formando una curva difícil de analizar. |
¿Cómo se leen los Puntos en una Gráfica Logarítmica?
Leer valores en una gráfica logarítmica es un poco diferente a leerlos en una gráfica normal, pero no es complicado. Se llama interpolación.
Imagina que tienes una gráfica logarítmica donde la distancia entre el 100 y el 1000 es de 50 milímetros. Si un punto está a 29 milímetros por encima del 100, ¿qué valor representa?
Para resolverlo, usamos la idea de que la proporción de distancias en la gráfica es igual a la proporción de los logaritmos de los números.
1. Calcula la proporción lineal: Divide la distancia desde el número más bajo (100) hasta tu punto (29 mm) entre la distancia total de la "década" (50 mm). * Proporción lineal = 29 mm / 50 mm = 0,58
2. Usa los logaritmos: La misma proporción debe ser cierta para los logaritmos de los números. * Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{\log(X) - \log(100)}{\log(1000) - \log(100)} * Donde X es el valor que buscamos.
3. Iguala las proporciones: * 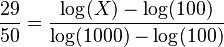
4. Resuelve la ecuación: * Sabemos que Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \log(1000) - \log(100) = \log(1000/100) = \log(10) = 1 . * Entonces, la ecuación se simplifica a: 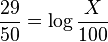 * Esto es: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 0,58 = \log \frac {X}{100} * Para quitar el logaritmo, usamos la potencia de 10: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 10^{0,58} = \frac {X}{100} * Calculamos Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 10^{0,58} , que es aproximadamente 3,802. * Entonces: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3,802 = \frac {X}{100} * Finalmente, multiplicamos por 100: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): X = 380,2
* Esto es: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 0,58 = \log \frac {X}{100} * Para quitar el logaritmo, usamos la potencia de 10: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 10^{0,58} = \frac {X}{100} * Calculamos Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 10^{0,58} , que es aproximadamente 3,802. * Entonces: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3,802 = \frac {X}{100} * Finalmente, multiplicamos por 100: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): X = 380,2
Así, el punto que está a 29 mm por encima del 100 en esa escala logarítmica representa el valor 380,2.
Véase también
 En inglés: Log–log plot Facts for Kids
En inglés: Log–log plot Facts for Kids
- representación semilogarítmica