Teorema de Lagrange (teoría de grupos) para niños

El teorema de Lagrange es una idea importante en una parte de las matemáticas llamada teoría de grupos. Imagina que tienes un conjunto de cosas y una forma de combinarlas, como sumar números o girar objetos. Si este conjunto y su forma de combinar cumplen ciertas reglas, lo llamamos un "grupo".

Este teorema nos dice algo especial sobre los grupos que tienen un número finito de elementos (es decir, que podemos contarlos). Si tienes un grupo grande llamado G y dentro de él hay un grupo más pequeño llamado H (al que llamamos "subgrupo"), el teorema de Lagrange afirma que el número de elementos de H siempre divide al número de elementos de G.

En otras palabras, si el grupo G tiene 10 elementos y el subgrupo H tiene 2 elementos, entonces 2 divide a 10. Si H tuviera 3 elementos, no podría ser un subgrupo de G si G tiene 10 elementos, porque 3 no divide a 10.

El teorema se escribe así:

Donde:

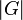• es el número de elementos del grupo G.
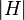• es el número de elementos del subgrupo H.
• es el "índice" de H en G, que es cuántas veces cabe H en G.

Aunque el teorema de Lagrange es siempre cierto, lo contrario no siempre lo es. Es decir, si un número divide al tamaño de un grupo, no significa que siempre exista un subgrupo de ese tamaño. Por ejemplo, hay un grupo llamado 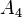que tiene 12 elementos, y aunque 6 divide a 12, este grupo no tiene ningún subgrupo con 6 elementos. Sin embargo, para algunos tipos especiales de grupos, como los grupos abelianos (donde el orden de las operaciones no importa) o los grupos cíclicos (que se generan a partir de un solo elemento), lo contrario sí es cierto.

Este teorema lleva el nombre del matemático italiano Joseph-Louis de Lagrange, quien lo dio a conocer en 1771.

¿Quién fue Joseph-Louis de Lagrange?

Joseph-Louis de Lagrange (1736-1813) fue un matemático y astrónomo muy importante. Nació en Italia, pero pasó gran parte de su vida en Francia y Prusia. Hizo contribuciones fundamentales en muchas áreas de las matemáticas, incluyendo el cálculo, la mecánica y la teoría de números. Su trabajo en la teoría de grupos, donde se encuentra este teorema, fue muy influyente y ayudó a sentar las bases para el desarrollo de las matemáticas modernas.

¿Cómo se demuestra el Teorema de Lagrange?

Para entender por qué el teorema de Lagrange es cierto, podemos imaginar que "dividimos" el grupo grande G en partes iguales usando el subgrupo H.

Pasos clave de la demostración

1. Definir una relación especial: Se crea una forma de relacionar los elementos de G entre sí, basada en el subgrupo H. Si tomas dos elementos, x e y, decimos que están relacionados si al combinar el inverso de x con y, el resultado está en H. 2. Formar "clases" o "cosets": Esta relación divide al grupo G en grupos más pequeños llamados "clases de equivalencia" o "cosets". Cada una de estas clases se forma multiplicando cada elemento de H por un elemento fijo de G. Por ejemplo, si g es un elemento de G, la clase Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): gH contiene todos los elementos que se obtienen al multiplicar g por cada elemento de H. 3. Tamaño de las clases: Se demuestra que todas estas clases tienen exactamente el mismo número de elementos que el subgrupo H. Si H tiene n elementos, entonces cada clase Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): gH también tiene n elementos. 4. Unión de las clases: El grupo G es como un rompecabezas formado por estas clases. Todas las clases son distintas y juntas cubren todo el grupo G sin superponerse. 5. Conclusión: Si G está formado por m de estas clases, y cada clase tiene el mismo número de elementos que H, entonces el número total de elementos en G es igual a m multiplicado por el número de elementos en H. Es decir, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): |G| = m \times |H| . Esto significa que 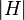siempre divide a 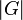, y m es el índice .

¿Qué consecuencias tiene el Teorema de Lagrange?

El teorema de Lagrange tiene varias consecuencias interesantes en la teoría de grupos:

• Orden de un elemento: Si tomas cualquier elemento de un grupo finito, el número de veces que necesitas combinarlo consigo mismo para volver al punto de partida (lo que se llama su "orden") siempre divide al número total de elementos del grupo.
• Grupos con número primo de elementos: Si un grupo tiene un número de elementos que es un número primo (como 5, 7, 11, etc.), entonces ese grupo es siempre un grupo cíclico. Esto significa que puedes encontrar un solo elemento en el grupo que, al combinarlo repetidamente consigo mismo, genera todos los demás elementos del grupo.
• Relación entre subgrupos: El teorema también ayuda a entender la relación entre el tamaño de dos subgrupos y su intersección (los elementos que tienen en común). Por ejemplo, si H y K son subgrupos de G, el tamaño del conjunto de todos los productos de un elemento de H y un elemento de K se puede calcular usando los tamaños de H, K y su intersección.
• Grupos de permutaciones: El teorema es útil para entender el tamaño de grupos importantes como el grupo simétrico (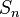), que contiene todas las formas posibles de ordenar n objetos. El tamaño de 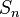es 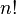(n factorial). También nos ayuda a saber que el subgrupo alternante (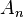), que es un subgrupo de 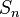, tiene exactamente la mitad de los elementos que .

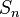¿Es el Teorema de Lagrange parte de algo más grande?

Sí, el teorema de Lagrange es un caso especial de una idea más general. Esta idea dice que si tienes un grupo G y dos subgrupos, H y K, donde K es un subgrupo de H, entonces la forma en que se relacionan sus índices es:

Esta fórmula es válida incluso si los grupos son infinitos. El teorema de Lagrange que conocemos se obtiene de esta fórmula general si consideramos que K es el subgrupo más pequeño posible, que solo contiene el elemento "neutro" del grupo (el que no cambia nada al combinarlo).

Véase también

En inglés: Lagrange's theorem (group theory) Facts for Kids