Distribución de Poisson para niños
Datos para niños Distribución de Poisson. |
||
|---|---|---|
=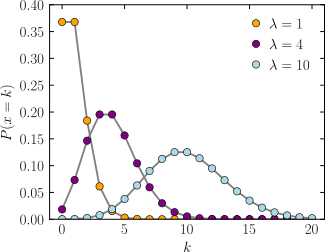 El eje horizontal es el índice x. La función solamente está definida en valores enteros de k. Las líneas que conectan los puntos son solo guías visuales y no indican continuidad. Función de densidad de probabilidad |
||
=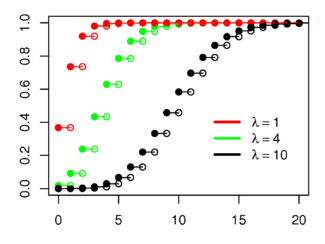 El eje horizontal es el índice k. Función de distribución de probabilidad |
||
| Parámetros | 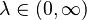 |
|
| Dominio | 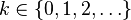 |
|
| Función de probabilidad (fp) | 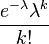 |
|
| Función de distribución (cdf) | 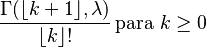 (donde Γ(x, y) es la función gamma incompleta) (donde Γ(x, y) es la función gamma incompleta) |
|
| Media | 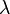 |
|
| Mediana | 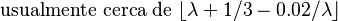 |
|
| Moda |  |
|
| Varianza | 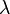 |
|
| Coeficiente de simetría | 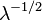 |
|
| Curtosis | 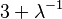 |
|
| Entropía | ![\lambda[1\!-\!\ln(\lambda)]\!+\!e^{-\lambda}\sum_{k=0}^\infty \frac{\lambda^k\ln(k!)}{k!}](/images/math/3/6/f/36f5766e9855c58b14b1b542b27c7812.png) |
|
| Función generadora de momentos (mgf) | 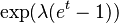 |
|
| Función característica | 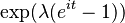 |
|
En teoría de probabilidad y estadística, la distribución de Poisson es una herramienta matemática que nos ayuda a calcular la probabilidad de que un evento ocurra un cierto número de veces en un período de tiempo específico. Es muy útil para eventos que suceden de forma rara o poco frecuente. También se puede usar para contar eventos en un área o volumen determinado.
Esta distribución fue presentada por Siméon-Denis Poisson en 1838. Él la dio a conocer en su trabajo Recherches sur la probabilité des jugements en matières criminelles et matière civile, donde investigaba la probabilidad de ciertos sucesos.
Por ejemplo, imagina un centro de llamadas que recibe un promedio de 180 llamadas por hora. Las llamadas llegan de forma independiente, es decir, una llamada no afecta la llegada de la siguiente. Si queremos saber cuántas llamadas se reciben en un minuto, podemos usar la distribución de Poisson. En este caso, el promedio sería de 3 llamadas por minuto. Los números más probables serían 2 o 3 llamadas, pero también es posible recibir 1 o 4, y hay una pequeña probabilidad de recibir 0 o incluso 10 llamadas.
Otro ejemplo es contar el número de eventos de cambio que ocurren en una fuente de energía durante un tiempo determinado.
Contenido
Historia de la Distribución de Poisson
La distribución de Poisson fue introducida por primera vez por el matemático Siméon Denis Poisson (1781-1840). La publicó junto con su teoría de la probabilidad en su obra Recherches sur la probabilité des jugements en matière criminelle et en matière civile en 1837. En este trabajo, Poisson estudió cómo contar el número de sucesos discretos (eventos) que ocurren en un intervalo de tiempo específico.
Curiosamente, un resultado similar ya había sido presentado en 1711 por Abraham de Moivre en su obra De Mensura Sortis seu; de Probabilitate Eventuum in Ludis a Casu Fortuito Pendentibus. Por esta razón, algunos expertos sugieren que la distribución de Poisson también debería llevar el nombre de Moivre.
En 1860, Simon Newcomb aplicó la distribución de Poisson para contar el número de estrellas en una unidad de espacio. Más tarde, en 1898, Ladislaus Bortkiewicz la usó para investigar el número de accidentes poco comunes en el ejército prusiano. Este estudio ayudó a que la distribución de Poisson se aplicara en campos como la ingeniería de la fiabilidad.
¿Qué es la Distribución de Poisson?
La distribución de Poisson es muy popular porque nos ayuda a modelar cuántas veces ocurre un evento en un período de tiempo o en un espacio.
Notación Matemática
Cuando decimos que una variable aleatoria (un valor que puede cambiar)  sigue una distribución de Poisson con un parámetro
sigue una distribución de Poisson con un parámetro  (lambda, que es un número mayor que 0), lo escribimos así:
(lambda, que es un número mayor que 0), lo escribimos así: 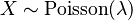 o
o 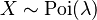 .
.
Función de Probabilidad
La fórmula principal para calcular la probabilidad de que un evento ocurra 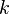 veces en una distribución de Poisson es:
veces en una distribución de Poisson es:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(k; \lambda) = \operatorname{P}(X{=}k)= \frac{\lambda^k e^{-\lambda}}{k!},
donde:
- k es el número de veces que ocurre el evento (puede ser 0, 1, 2, y así sucesivamente).
- e es el número de Euler, que es aproximadamente 2.71828.
- ! es la función factorial, que significa multiplicar un número por todos los enteros positivos menores que él (por ejemplo, 5! = 5 × 4 × 3 × 2 × 1).
Ejemplos de Uso
La distribución de Poisson puede ser útil para modelar situaciones como:
- El número de meteoritos de más de 1 metro de diámetro que chocan contra la Tierra en un año.
- El número de fotones de luz que llegan a un detector en un tiempo específico.
- El número de estudiantes que obtienen una nota muy baja o muy alta en un examen.
Cuándo Usar la Distribución de Poisson
La distribución de Poisson es un buen modelo si se cumplen estas condiciones:
- El número de veces que ocurre un evento (k) se puede contar (0, 1, 2, etc.).
- Que un evento ocurra no cambia la probabilidad de que ocurra otro. Los eventos son independientes.
- La velocidad promedio a la que ocurren los eventos es constante.
- No pueden ocurrir dos eventos exactamente al mismo tiempo. En un período muy pequeño, o ocurre un evento, o no ocurre ninguno.
Si estas condiciones se cumplen, entonces el número de eventos k puede ser modelado con una distribución de Poisson.
Esta distribución también es un caso especial de la distribución binomial cuando el número de intentos es muy grande y la probabilidad de éxito en cada intento es muy pequeña.
Propiedades Clave de la Distribución de Poisson
Si una variable aleatoria  sigue una distribución de Poisson con parámetro
sigue una distribución de Poisson con parámetro  , tiene algunas características importantes.
, tiene algunas características importantes.
Media (Promedio)
La media o el promedio de eventos que esperamos que ocurran es igual a  .
.
Esto significa que  no solo es un parámetro, sino también el valor promedio esperado de los eventos.
no solo es un parámetro, sino también el valor promedio esperado de los eventos.
Varianza
La varianza (que mide cuánto se dispersan los datos alrededor de la media) de una distribución de Poisson también es igual a  .
.
Esto es una característica especial de la distribución de Poisson: su media y su varianza son iguales.
Moda
La moda es el valor que tiene la mayor probabilidad de ocurrir. En la distribución de Poisson, la moda es el número entero más grande que es menor o igual a  . Se escribe como
. Se escribe como 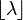 .
.
Relación con Otras Distribuciones
Suma de Variables de Poisson
Si sumamos varias variables aleatorias de Poisson que son independientes, el resultado es otra variable aleatoria de Poisson. El nuevo parámetro  será la suma de los parámetros de las variables originales.
será la suma de los parámetros de las variables originales.
Conexión con la Distribución Binomial
La distribución de Poisson es un caso especial de la distribución binomial. Esto ocurre cuando tenemos muchos intentos (n tiende a infinito) y la probabilidad de éxito en cada intento (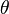 ) es muy pequeña, pero el producto de n y
) es muy pequeña, pero el producto de n y 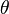 (que es
(que es  ) se mantiene constante.
) se mantiene constante.
Aproximación a la Distribución Normal
Cuando el valor de  es grande, la distribución de Poisson se parece mucho a una distribución normal (la famosa "campana de Gauss"). Esto es una consecuencia del teorema central del límite.
es grande, la distribución de Poisson se parece mucho a una distribución normal (la famosa "campana de Gauss"). Esto es una consecuencia del teorema central del límite.
Ejemplo Práctico
Imagina que el 2% de los libros encuadernados en un taller tienen un defecto. Si queremos saber la probabilidad de que 5 de 400 libros encuadernados tengan defectos, podemos usar la distribución de Poisson.
Aquí,  (el número de libros defectuosos que nos interesa). El valor esperado de libros defectuosos (
(el número de libros defectuosos que nos interesa). El valor esperado de libros defectuosos ( ) es el 2% de 400, que es 8. Entonces, la probabilidad se calcula así:
) es el 2% de 400, que es 8. Entonces, la probabilidad se calcula así:
Esto significa que hay aproximadamente un 9.2% de probabilidad de que 5 de esos 400 libros tengan defectos.
Procesos de Poisson
La distribución de Poisson se usa para modelar muchos fenómenos que ocurren en la naturaleza o en la vida diaria. Estos son eventos que se pueden contar (0, 1, 2, 3, etc.) en un tiempo o área definida, y donde la probabilidad de que ocurran es constante. Algunos ejemplos son:
- El número de coches que pasan por un punto en una carretera en un tiempo determinado.
- El número de errores de ortografía en una página escrita.
- El número de llamadas telefónicas que llegan a una central telefónica por minuto.
- El número de veces que se accede a un servidor web por minuto.
- El número de cambios en una cadena de ADN después de cierta exposición.
- El número de núcleos atómicos inestables que se transforman en un período dado.
- El número de estrellas en un volumen específico del espacio.
|
Véase también
 En inglés: Poisson distribution Facts for Kids
En inglés: Poisson distribution Facts for Kids



![\operatorname{E}[X]=\lambda](/images/math/f/6/0/f60e2b602e8d8c561f3d2ba28f853030.png)
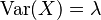
![\operatorname{P}[X=5]= \frac{8^5e^{-8}}{5!}=0.092](/images/math/1/6/1/161c9b2dce7fd2378d8bfccff2292bb0.png)