Esperanza (matemática) para niños
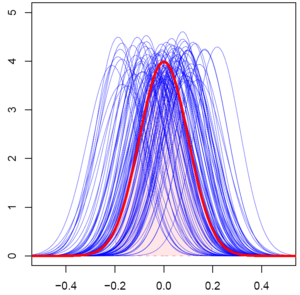
En matemática, especialmente en la rama de la estadística, la esperanza (también conocida como valor esperado o media) de una variable aleatoria es un número que nos ayuda a entender cuál es el valor promedio que se espera obtener de un evento que depende del azar. Es como calcular el promedio de un grupo de datos, pero aplicado a situaciones donde los resultados no son seguros.
Imagina que lanzas un dado de seis caras. Cada cara tiene la misma probabilidad de salir (1 de 6). Si lanzas el dado muchas veces, ¿qué número esperarías obtener en promedio? La esperanza matemática nos ayuda a calcular esto. Para un dado, la esperanza es 3.5. Aunque no puedes sacar un 3.5 en un dado, este número representa el promedio a largo plazo si lanzaras el dado muchísimas veces.
La esperanza matemática es muy útil en diferentes campos, como en los juegos de azar, para entender si un juego es "justo" o si tiende a favorecer a alguien a largo plazo.
Contenido
¿Qué es la Esperanza Matemática?
La esperanza matemática es el valor promedio que se espera de un resultado cuando un evento aleatorio se repite muchas veces. Es una forma de predecir el resultado más probable a largo plazo.
¿Cómo se calcula la Esperanza?
Para calcular la esperanza de una variable aleatoria discreta (que tiene un número limitado de resultados posibles, como un dado o una moneda), se multiplica cada posible resultado por la probabilidad de que ocurra, y luego se suman todos esos productos.
Por ejemplo, para el dado de 6 caras:
- El número 1 tiene una probabilidad de 1/6.
- El número 2 tiene una probabilidad de 1/6.
- Y así sucesivamente hasta el número 6.
La esperanza se calcula así: (1 * 1/6) + (2 * 1/6) + (3 * 1/6) + (4 * 1/6) + (5 * 1/6) + (6 * 1/6) = 3.5
Este cálculo nos da el valor promedio esperado.
Esperanza en los Juegos de Azar
En los juegos de azar, la esperanza matemática ayuda a saber si un juego es equilibrado. Por ejemplo, en un juego de ruleta con 37 casillas, si apuestas 1 euro a un solo número y ganas, recibes 35 euros. La esperanza matemática de tu beneficio por apostar 1 euro es aproximadamente -0.027 euros. Esto significa que, en promedio, por cada euro que apuestas, esperarías perder unos 2.7 céntimos. Un juego donde el beneficio esperado es cero se considera un "juego justo".
Historia de la Esperanza Matemática
La idea de la esperanza matemática surgió a mediados del siglo XVII a partir de un problema llamado "el problema de los puntos". Este problema buscaba cómo repartir las ganancias de un juego entre dos jugadores si el juego se detenía antes de tiempo.
Los Pioneros de la Probabilidad
El problema fue planteado por el escritor francés Chevalier de Méré al matemático Blaise Pascal en 1654. Pascal, junto con Pierre de Fermat, otro gran matemático, trabajaron en el problema. Ambos llegaron a la misma idea fundamental: el valor de una ganancia futura debe ser proporcional a la posibilidad de obtenerla.
Aunque no publicaron sus hallazgos de inmediato, compartieron sus ideas con otros científicos. Poco después, en 1657, el matemático neerlandés Christiaan Huygens publicó un libro llamado "De ratiociniis in ludo aleæ" (Sobre los cálculos en los juegos de azar). Este libro amplió el concepto de la esperanza y se considera uno de los primeros intentos exitosos de establecer las bases de la teoría de la probabilidad.
El Término "Esperanza Matemática"
Ni Pascal ni Huygens usaron la palabra "esperanza" en el sentido moderno. Fue más de cien años después, en 1814, cuando Pierre-Simon Laplace publicó su obra "Théorie analytique des probabilités", donde definió explícitamente el concepto de "esperanza matemática". Él explicó que es el producto de la suma esperada por la probabilidad de obtenerla.
Símbolos para la Esperanza
Para representar la esperanza matemática, se usa comúnmente la letra E. Esta letra viene de la palabra "Expectation" en inglés, "Erwartungswert" en alemán, y "Esperanza" en español.
Puedes verla escrita de varias maneras, como:
- E(X)
- E[X]
![\mathbb{E}[X]](/images/math/2/7/f/27f660bfd70f4a5d381949da7bcc5a85.png)
También se usa a veces la letra griega Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mu_X (mu sub X) o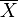 
(X con una barra encima), especialmente en física.
Propiedades de la Esperanza
La esperanza matemática tiene algunas propiedades importantes que la hacen muy útil en los cálculos:
- Esperanza de una constante: Si tienes un número fijo (una constante), su esperanza es ese mismo número. Por ejemplo, E[5] = 5.
- Multiplicación por una constante: Si multiplicas una variable aleatoria por un número, la esperanza de ese resultado es el número multiplicado por la esperanza de la variable. Por ejemplo, E[2X] = 2 * E[X].
- Suma de esperanzas: La esperanza de la suma de dos variables aleatorias es igual a la suma de sus esperanzas individuales. E[X + Y] = E[X] + E[Y]. Esto se llama linealidad y es una propiedad muy poderosa.
- Independencia: Si dos variables aleatorias son independientes (es decir, el resultado de una no afecta a la otra), la esperanza de su producto es el producto de sus esperanzas. E[XY] = E[X] * E[Y].
Es importante saber que no todas las variables aleatorias tienen un valor esperado. Algunas distribuciones de probabilidad, por su naturaleza, no tienen una esperanza definida.
Galería de imágenes
-
En matemática, la esperanza de una variable aleatoria X, es el número que formaliza la idea de valor medio de un fenómeno aleatorio.
Véase también
En inglés: Expected value Facts for Kids
