Distribución uniforme continua para niños
Datos para niños Uniforme |
||
|---|---|---|
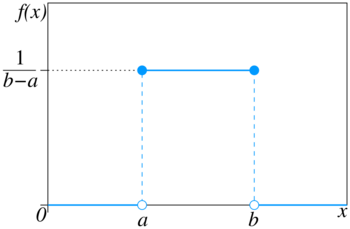 Utilizando convención de máximo Función de densidad de probabilidad |
||
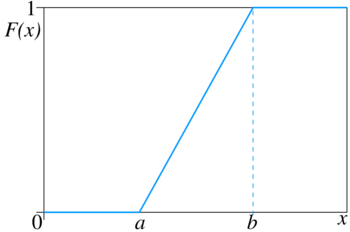 Función de distribución de probabilidad |
||
| Parámetros | 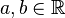 |
|
| Dominio | ![x\in[a,b]](/images/math/8/2/9/8290bddba5acf9822dcbf61f4ac67d1b.png) |
|
| Función de densidad (pdf) | 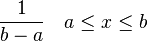 |
|
| Función de distribución (cdf) | 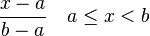 |
|
| Media | 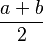 |
|
| Mediana | 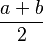 |
|
| Moda | cualquier valor en ![[a,b] \,\!](/images/math/8/b/5/8b596d04e319e05cadcc7dcf251a9815.png) |
|
| Varianza | 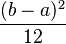 |
|
| Coeficiente de simetría | 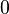 |
|
| Curtosis |  |
|
| Entropía | 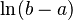 |
|
| Función generadora de momentos (mgf) |
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{e^{tb}-e^{ta</td></tr><tr><td class="noprint" colspan="3" style="text-align:left;"></td></tr></table><!--IB_END-->{t(b-a)} \,\! |car = En el mundo de la teoría de probabilidad y la estadística, la distribución uniforme continua es un tipo de distribución de probabilidad para números que pueden tomar cualquier valor dentro de un rango. Imagina que tienes un juego donde todos los resultados posibles entre un valor mínimo y uno máximo tienen la misma oportunidad de ocurrir. Eso es una distribución uniforme continua. Esta distribución se define por dos números: `a` (el valor más bajo) y `b` (el valor más alto). El rango puede incluir o no incluir `a` y `b`. A menudo se escribe como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): U(a,b) , donde la `U` significa "uniforme". La idea principal es que cualquier parte del rango que tenga la misma longitud es igual de probable. Contenido¿Qué es la distribución uniforme continua?Notación y cómo se representaCuando hablamos de una variable aleatoria continua que sigue una distribución uniforme, lo escribimos así: Función de densidad de probabilidad (FDP)La función de densidad de probabilidad (FDP) nos dice qué tan probable es encontrar un valor en un punto específico dentro del rango. Para una distribución uniforme continua, esta función es muy sencilla:
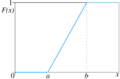
Esto es válido para cualquier valor `x` que esté entre `a` y `b`. Fuera de ese rango, la probabilidad es cero. Piensa en la FDP como un rectángulo. La base de este rectángulo es la distancia entre `a` y `b` (es decir, `b-a`), y la altura es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{1}{b-a} . Si el rango es más grande, la altura del rectángulo es más pequeña, lo que significa que la probabilidad de caer en un punto exacto es menor. Función de distribución acumulada (FDA)La función de distribución acumulada (FDA) nos dice la probabilidad de que una variable aleatoria sea menor o igual a un valor específico. Para la distribución uniforme continua, se calcula así: Esto significa que si `x` es menor que `a`, la probabilidad es 0. Si `x` es mayor o igual que `b`, la probabilidad es 1 (es decir, es seguro que el valor estará dentro o antes de ese punto). Y si `x` está entre `a` y `b`, la probabilidad aumenta de forma constante. Ejemplo 1: Calcular una probabilidadImagina que tienes una variable `X` que sigue una distribución uniforme entre 0 y 23, es decir, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): X \sim U(0,23) . ¿Cuál es la probabilidad de que `X` esté entre 2 y 18?
Esto significa que hay una probabilidad de 16/23 (aproximadamente 0.696) de que `X` caiga en ese intervalo. En un gráfico, esto sería el área de un rectángulo con base 16 y altura 1/23. Ejemplo 2: Probabilidad condicionalAhora, con la misma variable Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): X \sim U(0,23) , ¿cuál es la probabilidad de que `X` sea mayor que 12, sabiendo que ya es mayor que 8? Esto se llama probabilidad condicional.
Aquí, el rango de posibilidades cambia. Como ya sabemos que `X` es mayor que 8, nuestro nuevo punto de inicio es 8. Así, el nuevo rango va de 8 a 23. La probabilidad es 11/15. Características importantesMedia (promedio)La media o promedio de una variable aleatoria `X` con distribución uniforme entre `a` y `b` es simplemente el punto medio del intervalo: Si dibujas la función de densidad, verás que la media está justo en el centro del rectángulo. Varianza (dispersión)La varianza nos dice qué tan dispersos están los datos alrededor de la media. Para una distribución uniforme, la varianza de `X` es: Cuanto mayor sea la diferencia entre `b` y `a`, mayor será la varianza, lo que significa que los datos están más extendidos. UniformidadUna característica clave de esta distribución es que la probabilidad de que un valor caiga en un intervalo de cierta longitud es siempre la misma, sin importar dónde esté ese intervalo, siempre y cuando esté dentro del rango `[a,b]`. Por ejemplo, la probabilidad de que un valor esté entre 1 y 3 es la misma que entre 5 y 7, si ambos intervalos tienen la misma longitud y están dentro del rango total. Distribución uniforme estándarUn caso especial muy importante es cuando `a=0` y `b=1`. A esto se le llama distribución uniforme estándar, y se escribe Para esta distribución, las cosas se simplifican mucho:
SimetríaSi tienes una variable `X` que sigue una distribución uniforme estándar Transformada integral de probabilidadUn uso muy útil de la distribución uniforme estándar es para simular valores aleatorios de otras distribuciones. Si tienes una variable aleatoria `Y` con una función de distribución `F_Y`, puedes transformar `Y` para obtener una variable `X` que sigue una distribución uniforme estándar. Esto es muy útil en simulaciones por computadora. Aplicaciones prácticasMuestreo de una distribución uniformeEn la estadística y la simulación, a menudo necesitamos generar números aleatorios. Muchos lenguajes de programación tienen funciones que crean números pseudoaleatorios que se distribuyen de manera uniforme estándar (entre 0 y 1). Si tienes un número `u` generado de una distribución uniforme estándar, puedes transformarlo para que siga cualquier otra distribución uniforme `U(a,b)` usando la fórmula: `a + (b - a) * u`. Muestreo de una distribución cualquieraLa distribución uniforme es la base para generar números aleatorios que sigan casi cualquier otra distribución. Un método común es el método de muestreo de transformación inversa. Este método usa la función de distribución acumulada de la distribución que quieres simular. Por ejemplo, para la distribución normal, que es muy común, existe un método llamado Método de Box-Muller que usa dos variables aleatorias uniformes para generar dos variables aleatorias normales. Error de cuantificaciónCuando se convierte una señal analógica (como el sonido) a digital, se produce un pequeño error llamado error de cuantificación. Este error se debe a que los valores se redondean. Si la señal original es mucho más grande que el paso de redondeo, este error se distribuye de forma aproximadamente uniforme. Historia de la distribución uniformeAunque no se sabe con exactitud cuándo se empezó a hablar de la distribución uniforme, se cree que la idea de "uniforme" o "equiprobable" (que todos los resultados tienen la misma probabilidad) viene de los juegos de dados. En el siglo XVI, Gerolamo Cardano escribió un manual llamado Liber de Ludo Aleae donde hablaba de la probabilidad en los juegos de dados, lo que sentó las bases para entender la equiprobabilidad. Galería de imágenesVéase también |
|


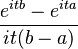 }}
}}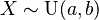 o Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): X\sim\operatorname{Unif}(a,b) . Esto significa que la variable `X` puede tomar cualquier valor entre `a` y `b` con la misma probabilidad.
o Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): X\sim\operatorname{Unif}(a,b) . Esto significa que la variable `X` puede tomar cualquier valor entre `a` y `b` con la misma probabilidad.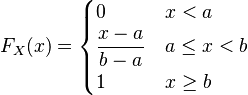
![\operatorname{E}[X]=\frac{a+b}{2}](/images/math/8/2/1/8214baf512a8f65405d8bcc829e8cc0c.png)
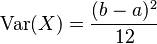
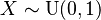 .
.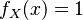 para cualquier `x` entre 0 y 1.
para cualquier `x` entre 0 y 1.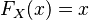 para `x` entre 0 y 1.
para `x` entre 0 y 1. .
.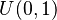 , entonces `1-X` también sigue una distribución uniforme estándar
, entonces `1-X` también sigue una distribución uniforme estándar 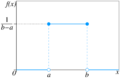
 En inglés:
En inglés: