Distribución uniforme discreta para niños
La distribución uniforme discreta es un concepto de la probabilidad y la estadística que nos ayuda a entender situaciones donde todos los resultados posibles tienen la misma oportunidad de ocurrir. Imagina que tienes un grupo de cosas y quieres elegir una al azar; si cada una de esas cosas tiene exactamente la misma probabilidad de ser elegida, entonces estás frente a una distribución uniforme discreta.
Un ejemplo muy sencillo es lanzar un dado de seis caras. Los números que pueden salir son 1, 2, 3, 4, 5 o 6. Cada vez que lanzas el dado, la probabilidad de que salga cualquiera de esos números es la misma: 1 de 6. Esto significa que el dado sigue una distribución uniforme discreta.
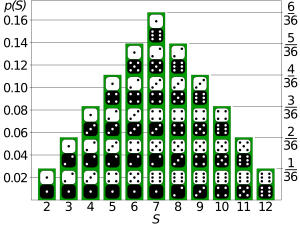
Pero, si lanzas dos dados y sumas los números que salen, la situación cambia. Por ejemplo, es más fácil obtener un 7 (sumando 1+6, 2+5, 3+4, etc.) que un 2 (solo 1+1). En este caso, la suma de los dos dados ya no sigue una distribución uniforme, porque no todos los resultados tienen la misma probabilidad.
Aunque a menudo hablamos de la distribución uniforme discreta con números enteros (como los de un dado), también puede aplicarse a cualquier grupo finito de elementos. Por ejemplo, si tienes una baraja de cartas bien mezclada, la probabilidad de sacar cualquier carta específica es la misma.
Contenido
¿Qué es una Distribución Uniforme Discreta?
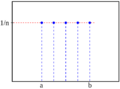
Una distribución uniforme discreta ocurre cuando tienes un número limitado de resultados posibles y cada uno de ellos tiene exactamente la misma probabilidad de suceder. Es como si la "suerte" se repartiera de manera igual entre todas las opciones.
¿Cómo se representa?
Cuando hablamos de una variable aleatoria (algo cuyo valor es un resultado de un evento al azar) que sigue una distribución uniforme discreta, podemos escribirlo de una forma especial. Si tenemos un conjunto de resultados posibles, por ejemplo, {x1, x2, ..., xn}, y cada uno tiene la misma probabilidad, decimos que la variable sigue una distribución uniforme.
La probabilidad de cada resultado
En una distribución uniforme discreta, la probabilidad de que ocurra cualquiera de los resultados es siempre la misma. Si hay 'n' resultados posibles, la probabilidad de que ocurra uno específico es 1 dividido por 'n'. Por ejemplo, en un dado de 6 caras, n=6, así que la probabilidad de que salga un 3 es 1/6.
Características Importantes
Las variables que siguen una distribución uniforme discreta tienen algunas características especiales que nos ayudan a entenderlas mejor.
El promedio (Media)
La media, o el promedio, de una distribución uniforme discreta es el valor central de todos los resultados posibles. Si sumas todos los resultados y los divides por la cantidad de resultados, obtendrás la media. Por ejemplo, para un dado (1, 2, 3, 4, 5, 6), la media es (1+2+3+4+5+6)/6 = 3.5.
La dispersión (Varianza)
La varianza nos dice qué tan dispersos o separados están los resultados de la media. Si los resultados están muy juntos, la varianza es pequeña. Si están muy separados, la varianza es grande. En una distribución uniforme discreta, la varianza se calcula de una manera específica, pero lo importante es saber que nos da una idea de la variedad de los resultados.
¿Qué pasa al sumar resultados?
Cuando sumas los resultados de dos eventos que siguen una distribución uniforme discreta, el resultado ya no es uniforme. Por ejemplo, al sumar dos dados, la probabilidad de obtener un 7 es mayor que la de obtener un 2 o un 12. Esto se debe a que hay más combinaciones que suman 7 que las que suman 2 o 12.
Ejemplos Cotidianos
La distribución uniforme discreta se ve en muchos lugares:
- Un dado perfecto: Cada cara (1, 2, 3, 4, 5, 6) tiene una probabilidad de 1/6 de salir.
- Una moneda perfecta: Cada lado (cara o cruz) tiene una probabilidad de 1/2 de salir.
El problema del tanque alemán
Durante la Segunda Guerra Mundial, los Aliados usaron la distribución uniforme discreta para estimar cuántos tanques producían los alemanes. Si capturaban algunos tanques y veían sus números de serie (por ejemplo, 3, 7, 12), y sabían que los tanques se numeraban desde el 1 en adelante, podían usar una fórmula para estimar el número total de tanques producidos.
La idea era que si los números de serie se distribuían de manera uniforme, el número más alto que encontraban en los tanques capturados (el "máximo de la muestra") les daría una pista sobre el número total de tanques. Los resultados de este método fueron sorprendentemente precisos, mucho más que las estimaciones de inteligencia tradicionales.
Por ejemplo, en junio de 1940, la estimación estadística basada en los números de serie fue de 169 tanques, mientras que la inteligencia tradicional estimó 1000. El registro alemán real fue de 122. Aunque no siempre era exacto, el método estadístico solía ser mucho más cercano a la realidad.
| Mes | Estimación estadística | Estimación de inteligencia | Registro alemán |
| Junio de 1940 | 169 | 1000 | 122 |
| Junio de 1941 | 244 | 1550 | 271 |
| Agosto de 1942 | 327 | 1550 | 342 |
¿Cómo evitar que te descubran?
Para evitar que otros usen los números de serie para estimar la producción, se pueden tomar medidas. Una forma es no usar números de serie secuenciales o hacerlos muy difíciles de descifrar. Por ejemplo, se pueden usar números aleatorios muy grandes o encriptar los números de serie.
Un ejemplo de esto se ve en una novela donde los números de serie de un cohete se encriptan usando una palabra clave. Cada letra de la palabra clave representa un número, y así, el número de serie real se convierte en una combinación de letras. Esto hace que sea mucho más difícil para alguien externo adivinar el número total de objetos producidos.
| H | U | N | T | S | V | I | L | E | X |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
En este ejemplo, la palabra clave es "Huntsville" (sin letras repetidas). Así, el cohete número 13 se escribiría como "HN" (H=1, N=3), y el número 24 como "UT" (U=2, T=4).
Galería de imágenes
Véase también
 En inglés: Discrete uniform distribution Facts for Kids
En inglés: Discrete uniform distribution Facts for Kids