Distribución exponencial para niños
Datos para niños Distribución exponencial |
||
|---|---|---|
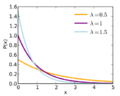
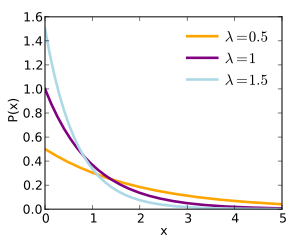 Función de densidad de probabilidad |
||
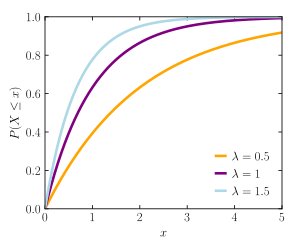 Función de distribución de probabilidad |
||
| Parámetros |  |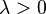
|
| Dominio |  |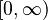
|
| Función de densidad (pdf) |  |
|
| Función de distribución (cdf) |  |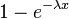
|
| Media |  |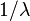
|
| Mediana |  |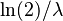
|
| Moda |  |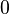
|
| Varianza |  |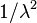
|
| Coeficiente de simetría |  |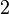
|
| Curtosis |  |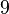
|
| Entropía |  |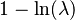
|
| Función generadora de momentos (mgf) |  |
|
| Función característica |  |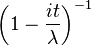
|
En el mundo de la probabilidad y la Estadística, la distribución exponencial es una herramienta matemática muy útil. Se usa para predecir cuánto tiempo tendremos que esperar hasta que ocurra un evento. Imagina que estás esperando algo, como la próxima llamada en un centro de atención o el siguiente terremoto. Esta distribución nos ayuda a entender esos tiempos de espera.
Una característica especial de la distribución exponencial es que no tiene "memoria". Esto significa que el tiempo que ya ha pasado esperando no afecta el tiempo que aún queda por esperar. Es como si cada momento fuera un nuevo comienzo.
Contenido
¿Qué es la Distribución Exponencial?
La distribución exponencial es un tipo de distribución de probabilidad continua. Esto significa que se aplica a cosas que se pueden medir, como el tiempo, y que pueden tomar cualquier valor dentro de un rango.
¿Cómo se define?
Una variable aleatoria (un valor que puede cambiar) se dice que sigue una distribución exponencial si su comportamiento se puede describir con una fórmula específica. Esta fórmula usa un número llamado "parámetro" (representado por la letra griega lambda, 
). Este parámetro es clave porque nos dice qué tan rápido ocurren los eventos.
- Si es grande, los eventos ocurren más seguido.
- Si es pequeño, los eventos ocurren con menos frecuencia.
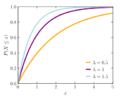
La fórmula principal que describe cómo se distribuyen las probabilidades se llama función de densidad de probabilidad. Otra fórmula importante es la función de distribución acumulada, que nos dice la probabilidad de que un evento ocurra antes de un cierto tiempo.
Propiedades Clave de la Distribución Exponencial
La distribución exponencial tiene algunas propiedades interesantes que la hacen única y útil.
La Propiedad de "Pérdida de Memoria"
Esta es la característica más famosa de la distribución exponencial. Significa que el pasado no influye en el futuro. Por ejemplo, si un autobús llega cada 10 minutos en promedio, y ya has esperado 5 minutos, la probabilidad de que llegue en los próximos 5 minutos es la misma que si acabaras de llegar a la parada. Es como si el "reloj" se reiniciara en cada momento.
- Imagina que tienes una bombilla que dura un tiempo que sigue una distribución exponencial. Si la bombilla ya ha funcionado durante 100 horas, la probabilidad de que dure 50 horas más es la misma que la probabilidad de que una bombilla nueva dure 50 horas. No "recuerda" cuánto tiempo ha estado encendida.
Media y Varianza
Para una distribución exponencial, la media (el valor promedio esperado) es simplemente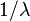 
. La varianza (que mide cuánto se dispersan los datos alrededor de la media) es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1/\lambda^2 . Estos valores nos ayudan a entender el comportamiento típico de los tiempos de espera.
Ejemplos de Uso de la Distribución Exponencial
La distribución exponencial se usa en muchos campos para modelar situaciones de la vida real.
- Tiempo de espera en un centro de llamadas: ¿Cuánto tiempo pasará hasta que recibamos la primera llamada del día?
- Intervalos entre eventos naturales: El tiempo entre terremotos de cierta magnitud o erupciones volcánicas.
- Defectos en la producción: La cantidad de metros de alambre que se producen hasta encontrar una falla.
- Fiabilidad de sistemas: El tiempo que un dispositivo electrónico funciona correctamente antes de fallar, si su tasa de fallo es constante.
Distribuciones Relacionadas
La distribución exponencial está conectada con otras distribuciones importantes en estadística:
- Es un caso especial de la distribución Gamma.
- Si sumamos varias variables aleatorias independientes que siguen una distribución exponencial, el resultado es una Distribución de Erlang.
Aplicaciones Prácticas
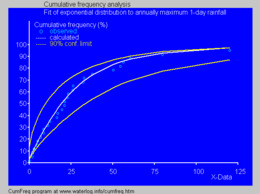
En campos como la hidrología (el estudio del agua), la distribución exponencial se usa para analizar eventos extremos. Por ejemplo, puede ayudar a predecir la probabilidad de lluvias diarias muy intensas.
La imagen muestra cómo se puede ajustar esta distribución a datos reales, como las lluvias máximas diarias de un año. Esto nos permite hacer predicciones y entender mejor los patrones.
Cómo Generar Números Aleatorios Exponenciales
En computación, a veces necesitamos simular eventos que siguen una distribución exponencial. Para esto, se usan algoritmos especiales que toman números aleatorios uniformes (donde cada número tiene la misma probabilidad de aparecer) y los transforman en números que siguen una distribución exponencial.
- Una fórmula común para generar un valor
con distribución exponencial a partir de un número aleatorio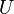 
(entre 0 y 1) es: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): X=-\frac{1}{\lambda} \ln (U) .
Véase también
En inglés: Exponential distribution Facts for Kids
- Proceso de Poisson
- Distribución Gamma
- Distribución de Erlang
- Distribución χ²
- Distribución Poisson
Software
Existen programas de computadora y herramientas de software que pueden ayudarte a trabajar con la distribución exponencial, como ajustar datos a esta distribución o calcular probabilidades:
- MathWorks Benelux
- Ricci distributions, fitting distributions with R
- Risksolver, automatically fit distributions and parameters to samples
- CumFreq [1], una herramienta gratuita que incluye intervalos de confianza.
Galería de imágenes
-
Función de densidad de probabilidad
-
Función de distribución de probabilidad
