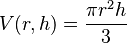Derivada parcial para niños
En matemáticas, la derivada parcial de una función con varias variables es una forma especial de calcular cómo cambia esa función cuando solo una de sus variables cambia, mientras las demás se mantienen fijas. Imagina que tienes una receta de cocina donde la cantidad de azúcar y harina afectan el sabor de un pastel. Si quieres saber cómo cambia el sabor solo por la cantidad de azúcar (manteniendo la harina igual), usarías una derivada parcial.
Las derivadas parciales se usan en áreas como el cálculo vectorial y la geometría diferencial, que nos ayudan a entender cómo se mueven las cosas o cómo son las formas en el espacio.
La derivada parcial de una función 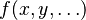 con respecto a la variable
con respecto a la variable  se puede escribir de varias maneras, como:
se puede escribir de varias maneras, como:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{\partial f}{\partial x},\partial_x f,\text{ o } f_x.
El símbolo 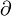 es como una 'd' redondeada y se conoce como la 'd de Jacobi'. Uno de los primeros en usar un símbolo parecido fue el Marqués de Condorcet en 1770. La forma moderna de escribir las derivadas parciales la propuso Adrien-Marie Legendre en 1786, y luego Carl Gustav Jacob Jacobi la volvió a usar en 1841.
es como una 'd' redondeada y se conoce como la 'd de Jacobi'. Uno de los primeros en usar un símbolo parecido fue el Marqués de Condorcet en 1770. La forma moderna de escribir las derivadas parciales la propuso Adrien-Marie Legendre en 1786, y luego Carl Gustav Jacob Jacobi la volvió a usar en 1841.
Cuando una cantidad  depende de varias variables (como
depende de varias variables (como 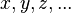 ), por ejemplo:
), por ejemplo:
Al calcular una derivada parcial, encontramos la inclinación de una línea que toca la función en un punto específico. Esta línea es paralela a un plano formado por el eje de la variable que estamos analizando y el eje que representa los valores de la función.
Contenido
¿Qué es una Derivada Parcial?
Entendiendo el Cambio en Funciones con Varias Variables
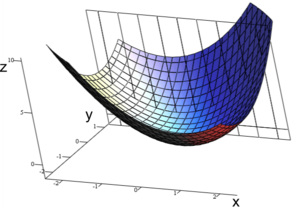
Imagina que tienes una función que describe una superficie en el espacio, como la altura de una montaña en diferentes puntos. Por ejemplo, la función 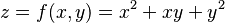 crea una forma curva en 3D.
crea una forma curva en 3D.
En cualquier punto de esta superficie, hay muchas direcciones en las que puedes moverte. La derivada parcial nos ayuda a encontrar la inclinación de la superficie si solo te mueves en una dirección específica, por ejemplo, solo hacia adelante o solo hacia los lados.
Generalmente, nos interesan las inclinaciones que son paralelas a los planos principales, como el plano Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): xz (donde la variable  se mantiene constante) o el plano
se mantiene constante) o el plano 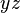 (donde la variable
(donde la variable  se mantiene constante).
se mantiene constante).
Calculando la Inclinación en un Punto Específico
Para encontrar la inclinación de la función Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(x,y)=x^2 + xy + y^2 en un punto como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): P(1,1) , si queremos saber cómo cambia la función solo con respecto a  (manteniendo
(manteniendo  constante), hacemos lo siguiente:
constante), hacemos lo siguiente:
1. Consideramos  como un número fijo. 2. Derivamos la función solo con respecto a
como un número fijo. 2. Derivamos la función solo con respecto a  .
.
La derivada parcial de  con respecto a
con respecto a  es:
es:
Ahora, si queremos saber la inclinación en el punto 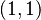 , reemplazamos
, reemplazamos  e Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y=1 en la expresión:
e Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y=1 en la expresión:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{\partial f}{\partial x}|_{(1,1)}=2(1)+1 = 3
Esto significa que en el punto 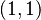 , si te mueves solo en la dirección de
, si te mueves solo en la dirección de  (manteniendo
(manteniendo  constante), la inclinación de la superficie es 3.
constante), la inclinación de la superficie es 3.
Ejemplos Prácticos de Derivadas Parciales
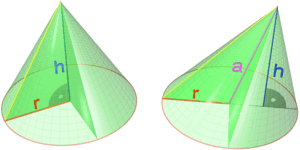
Volumen de un Cono
Un buen ejemplo para entender las derivadas parciales es el volumen de un cono. El volumen  de un cono depende de dos cosas: su altura
de un cono depende de dos cosas: su altura 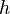 y el radio de su base
y el radio de su base  . La fórmula es:
. La fórmula es:
Podemos calcular cómo cambia el volumen si solo modificamos el radio o solo la altura:
- Cambio del volumen al variar el radio (altura constante):
Si queremos saber cómo cambia el volumen si solo aumentamos o disminuimos el radio, manteniendo la altura fija, calculamos la derivada parcial de  con respecto a
con respecto a  : :Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{\partial V}{\partial r}=\frac{2\pi rh}{3} Esto nos dice qué tan rápido crece o decrece el volumen si solo ajustamos el radio.
: :Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{\partial V}{\partial r}=\frac{2\pi rh}{3} Esto nos dice qué tan rápido crece o decrece el volumen si solo ajustamos el radio.
- Cambio del volumen al variar la altura (radio constante):
Si queremos saber cómo cambia el volumen si solo aumentamos o disminuimos la altura, manteniendo el radio fijo, calculamos la derivada parcial de  con respecto a
con respecto a 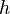 : :Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{ \partial V}{\partial h}=\frac{\pi r^2}{3} Esto nos dice qué tan rápido crece o decrece el volumen si solo ajustamos la altura.
: :Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{ \partial V}{\partial h}=\frac{\pi r^2}{3} Esto nos dice qué tan rápido crece o decrece el volumen si solo ajustamos la altura.
El Gradiente: La Dirección de Mayor Cambio
El gradiente es un concepto importante relacionado con las derivadas parciales. Imagina que estás en la superficie de una montaña y quieres saber en qué dirección es más empinada. El gradiente es un vector que apunta en la dirección donde la función (la altura de la montaña) aumenta más rápidamente.
Si tienes una función  que depende de varias variables (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x_1, x_2, \dots, x_n ), el gradiente de
que depende de varias variables (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x_1, x_2, \dots, x_n ), el gradiente de  en un punto se forma con todas sus derivadas parciales en ese punto:
en un punto se forma con todas sus derivadas parciales en ese punto:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \nabla f(a) = \left(\frac{\partial f}{\partial x_1}(a), \ldots, \frac{\partial f}{\partial x_n}(a)\right).
Este vector nos indica la dirección de mayor cambio de la función.
Notación de las Derivadas Parciales
Las derivadas parciales se pueden escribir de varias maneras. Si tenemos una función 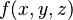 :
:
- Derivadas parciales de primer orden:
Con respecto a  , se pueden escribir como: :
, se pueden escribir como: :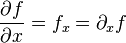
- Derivadas parciales de segundo orden:
Si derivamos dos veces con respecto a la misma variable, por ejemplo  : :Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{\partial^2 f}{\partial x^2}=f_{xx}=\partial_{xx}f
: :Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{\partial^2 f}{\partial x^2}=f_{xx}=\partial_{xx}f
- Derivadas parciales cruzadas:
Si derivamos primero con respecto a una variable y luego con respecto a otra, por ejemplo, primero  y luego
y luego  : :Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{\partial^2 f}{\partial y\partial x}=\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right)=f_{xy} Un dato interesante es que, si estas derivadas son "continuas" (es decir, no tienen saltos bruscos), el orden en que las calculas no importa. Es decir, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f_{xy} es igual a Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f_{yx} . Esto se conoce como el teorema de Clairaut o teorema de Schwarz.
: :Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{\partial^2 f}{\partial y\partial x}=\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right)=f_{xy} Un dato interesante es que, si estas derivadas son "continuas" (es decir, no tienen saltos bruscos), el orden en que las calculas no importa. Es decir, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f_{xy} es igual a Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f_{yx} . Esto se conoce como el teorema de Clairaut o teorema de Schwarz.
Derivada Direccional
La derivada direccional es una idea que va un paso más allá de la derivada parcial. Mientras que la derivada parcial mide el cambio en una dirección paralela a los ejes (como solo en  o solo en
o solo en  ), la derivada direccional mide el cambio de una función en CUALQUIER dirección que elijas.
), la derivada direccional mide el cambio de una función en CUALQUIER dirección que elijas.
Imagina que estás en la montaña y quieres saber qué tan empinada es si caminas en diagonal. La derivada direccional te daría esa información. Se calcula usando el gradiente y la dirección en la que quieres moverte.
Galería de imágenes
-
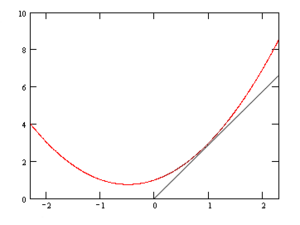
Una gráfica de Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): z = x^2 + xy + y^2 . Para la derivada parcial en Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (1, 1) que deja
 constante, la recta tangente correspondiente es paralela al plano Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): xz .
constante, la recta tangente correspondiente es paralela al plano Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): xz .
Véase también
 En inglés: Partial derivative Facts for Kids
En inglés: Partial derivative Facts for Kids


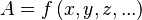
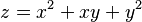 es una superficie curva.
es una superficie curva.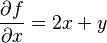
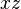 , en
, en  . La pendiente de la recta tangente es
. La pendiente de la recta tangente es 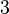 .
.