Deformación (ingeniería) para niños
En ingeniería, la deformación es el cambio de tamaño o forma que experimenta un objeto cuando se le aplica una fuerza. Imagina que estiras una goma elástica o aplastas una pelota de plastilina; esos son ejemplos de deformación.
Los "desplazamientos" son los cambios en la posición de un punto específico de un objeto. Las "deflexiones" son los cambios en la posición de los puntos de un objeto en relación con los puntos que tiene cerca.
Contenido
¿Qué es la Deformación y la Tensión?
La deformación se refiere a cómo cambia internamente un material, como si un pequeño cubo de ese material cambiara su longitud o los ángulos de sus lados. Se mide sin unidades, como un porcentaje de cambio.
Las deformaciones están relacionadas con las fuerzas que actúan sobre el material, a las que llamamos tensiones. Piensa en la tensión como la fuerza que se distribuye sobre una superficie. Para entender cómo un material reacciona a estas fuerzas, se hacen pruebas como estirarlo (ensayo de tracción) o aplastarlo (ensayo de compresión).
La Relación entre Tensión y Deformación
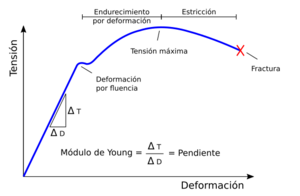
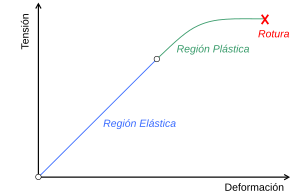
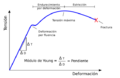
Generalmente, la relación entre la tensión y la deformación es directa y reversible. Esto significa que si aplicas una fuerza y el objeto se deforma, pero luego quitas la fuerza y el objeto vuelve a su forma original, decimos que la deformación es elástica. Esto ocurre hasta cierto punto. La relación directa entre la tensión y la deformación en esta etapa se conoce como módulo de Young.
Si la fuerza es demasiado grande y el objeto no vuelve a su forma original, sino que se queda con una nueva forma, entonces hablamos de deformación plástica. Es como cuando doblas un clip y se queda doblado.
Estudiar cómo se relacionan las tensiones y las deformaciones en los objetos sólidos es el campo de la resistencia de materiales. Cuando se trata de estructuras grandes, como puentes o edificios, se llama análisis estructural.
¿Cómo se Mide la Tensión y la Deformación?
La tensión y la deformación se calculan a partir de las fuerzas que actúan sobre un objeto y cómo cambia su forma. Si el objeto no cambia mucho de tamaño, estas medidas son bastante precisas.
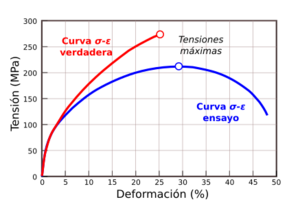
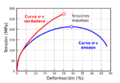
Sin embargo, si el objeto cambia mucho de tamaño, como un metal que se estira hasta volverse muy delgado, se usan conceptos más avanzados como la tensión verdadera y la deformación verdadera. Estas se calculan usando las dimensiones del objeto en cada momento, especialmente el área de su sección transversal.
En la imagen, puedes ver cómo una fuerza que aplasta (compresión, flecha azul) deforma un cilindro. La forma original (gris) se modifica a una forma con los lados abultados (rojo). Esto sucede porque el material es lo suficientemente fuerte como para no romperse, pero no para soportar la carga sin cambiar. Por eso, el material se expande hacia los lados.
Tipos de Deformación en Materiales
Dependiendo del material, su tamaño, su forma y las fuerzas aplicadas, un objeto puede deformarse de diferentes maneras.
La deformación puede ser:
- Permanente: El objeto no vuelve a su forma original después de quitar la fuerza. También se llama deformación plástica.
- Temporal: El objeto sí vuelve a su forma original después de quitar la fuerza. También se llama deformación elástica.
Deformación Elástica: ¿Cómo Vuelven los Objetos a su Forma?
La deformación elástica es muy importante en la ingeniería civil. Se estudia en materiales de construcción como el hormigón o el acero, que solo se deforman muy poquito. Para estos casos, se usa una teoría que asume que las deformaciones y los giros son muy pequeños.
Algunos materiales, como los elastómeros (piensa en la goma) o algunos polímeros, pueden estirarse mucho y aun así volver a su forma. Sin embargo, su elasticidad no es lineal, lo que significa que la relación entre la fuerza y la deformación no es tan sencilla.
Para materiales como la cerámica, los metales comunes, el hormigón y la mayoría de los cristales, la elasticidad es lineal y su rango elástico es más pequeño. Para ellos, se usa la ley de Hooke:
Aquí,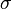 
es la tensión (la fuerza aplicada), 
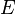es una constante del material llamada módulo de Young (que nos dice qué tan rígido es el material), y 
es la deformación resultante. Esta fórmula solo funciona en el rango elástico.
Es importante saber que no todos los materiales elásticos siguen esta ley de forma lineal. Algunos, como el hormigón o ciertos polímeros, se deforman de manera no lineal.
Tensión y Deformación Verdaderas: Más Allá de lo Simple
Cuando un material se estira mucho, su área transversal (el "grosor") cambia. Para tener una medida más precisa de la tensión y la deformación en estos casos, se usan la tensión y la deformación "verdaderas". Estas tienen en cuenta el área y la longitud del material en cada momento, no solo al principio.
Por ejemplo, la deformación verdadera se calcula usando el logaritmo del cambio de longitud:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \varepsilon_t = \ln \left (\frac{L_f}{L_0} \right )
Donde 
es la longitud final y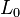 
es la longitud inicial.
Estas medidas más complejas nos ayudan a entender mejor cómo se comporta un material, especialmente cuando empieza a "estrecharse" (cuando una parte se vuelve mucho más delgada que el resto) o cuando la temperatura cambia.
Deformación Plástica: Cuando el Cambio es Permanente
La deformación plástica es un cambio permanente. Una vez que ocurre, el objeto no vuelve a su forma original, incluso si quitas la fuerza. Sin embargo, antes de la deformación plástica, el objeto siempre pasa por una deformación elástica, por lo que regresará un poco a su forma inicial.
Materiales como el cobre, la plata y el oro tienen un gran rango de deformación plástica, lo que significa que se pueden doblar o estirar mucho antes de romperse. El acero también se comporta así. En cambio, materiales como el vidrio o la cerámica tienen un rango de deformación plástica muy pequeño. Un ejemplo extremo de deformación plástica es la goma de mascar húmeda, que se puede estirar muchísimas veces su longitud original.
Cuando un material se estira y sufre deformación plástica, primero se vuelve más resistente (esto se llama endurecimiento por deformación) y luego una parte se empieza a hacer más delgada (esto se llama estricción o "cuello de botella"). Finalmente, el material se rompe.
Fatiga de los Metales: El Desgaste Invisible
La fatiga de materiales es un tipo de deformación que ocurre principalmente en metales que se pueden doblar (dúctiles). Aunque un material se deforme solo un poquito, dentro de su rango elástico, cada vez que se le aplica y se le quita una fuerza, ocurren pequeños daños a nivel molecular.
Después de muchos ciclos de carga y descarga, pueden aparecer grietas muy pequeñas que, con el tiempo, crecen hasta que el material se rompe, a veces sin que se vea una deformación plástica grande antes. Esto ha sido una causa importante de fallos en aviones, por ejemplo.
Para evitar la fatiga, se pueden reemplazar las piezas antes de que fallen o inspeccionarlas para detectar grietas muy pequeñas. Elegir materiales que no sufran fatiga durante la vida útil del producto es la mejor opción. También, evitar formas con esquinas muy afiladas ayuda, ya que estas concentran la tensión.
Rotura por Compresión: Cuando Algo se Aplasta
Cuando se aplica una fuerza de compresión a objetos largos y delgados, como columnas, estos se acortan. Si la fuerza es muy grande, el objeto puede fallar.
Los materiales dúctiles, como la mayoría de los metales, pueden "fluir" o deformarse mucho antes de romperse. Los materiales frágiles, como el hormigón, las rocas o el vidrio, se rompen de repente sin mucha deformación previa.
En columnas o barras delgadas, un aumento de la fuerza de compresión puede causar un pandeo (que se doblen o curven) mucho antes de que el material alcance su máxima resistencia a ser aplastado.
Fractura: El Punto de Ruptura
La fractura es otro tipo de deformación irreversible. Ocurre cuando un material ha pasado por sus etapas de deformación elástica y plástica, y las fuerzas se acumulan tanto que el material se rompe. Todos los materiales se fracturarán si se les aplica una fuerza lo suficientemente grande.
Conceptos Importantes sobre la Deformación
Un error común es pensar que los materiales que se doblan son "débiles" y los que no lo hacen son "fuertes". En realidad, muchos materiales que se deforman mucho (tanto elástica como plásticamente), como el acero, pueden absorber mucha energía sin romperse. En cambio, materiales frágiles como el vidrio, que no se doblan, pueden romperse fácilmente con menos fuerza porque tienen muy poca capacidad de deformación plástica.
Galería de imágenes
-
La tensión de compresión (azul) da como resultado una deformación que achata el objeto y lo expande hacia afuera, mientras que una tracción (rojo) lo alarga pero lo comprime hacia adentro
-
Diagrama típico de tensión frente a deformación que indica las distintas etapas de deformación de un material dúctil
-
Comparación de las curvas tensión-deformación verdaderas y de ensayo
-
Curva de tensión-deformación verdaderas de un metal con estructura atómica centrada en caras y su forma deducida
-
Diagramas tipo: (a) Curva tensión-deformación verdadera sin tangentes. No hay estiramiento ni estrechamiento. (b) Con una tangente. Solo hay estrechamiento. (c) Con dos tangentes. Hay estrechamiento y estiramiento.
-
Chapa de acero de baja aleación de alta resistencia marca Swebor, mostrando ambos lados, después de la deformación plástica producida por proyectiles en pruebas de balística.
-
Diagrama de un ensayo de tracción, mostrando la relación entre la tensión (fuerza aplicada) y el alargamiento (deformación) de un metal dúctil
Véase también
En inglés: Deformation Facts for Kids
