Resistencia de materiales para niños

La resistencia de materiales es una parte importante de la ingeniería mecánica, la ingeniería estructural, la ingeniería civil y la ingeniería de materiales. Esta área de estudio se encarga de entender cómo los objetos y las estructuras se comportan cuando se les aplican fuerzas. Imagina que quieres construir un puente o un edificio: necesitas saber si los materiales que usarás son lo suficientemente fuertes para soportar el peso y otras fuerzas sin romperse o deformarse demasiado.

La resistencia de materiales nos ayuda a predecir si un objeto puede soportar las fuerzas sin sufrir daños permanentes o romperse. Para ello, se usan modelos sencillos que relacionan las fuerzas aplicadas (también llamadas cargas) con los esfuerzos internos y los cambios de forma (desplazamientos) que esas fuerzas provocan en el material.

Cuando las formas de los objetos son muy complicadas, los ingenieros usan métodos más avanzados, como la teoría de la elasticidad o la mecánica de sólidos deformables. También pueden usar programas de computadora que emplean una técnica llamada análisis por elementos finitos para resolver problemas complejos.

¿Qué estudia la resistencia de materiales?

Cómo reacciona un material cuando se estira.

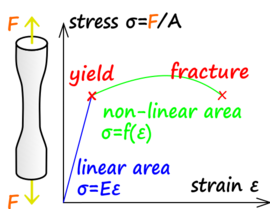
La resistencia de materiales se enfoca en cómo los objetos se deforman y qué tensiones (fuerzas internas por unidad de área) aparecen dentro de ellos cuando se les aplican cargas.

Para objetos con formas simples, como vigas (largas y delgadas), pilares (columnas) o placas y láminas (planas y delgadas), el estudio se puede simplificar mucho. En lugar de analizar cada punto del objeto en tres dimensiones, se pueden usar cálculos más sencillos que se aplican a una línea (para vigas) o a una superficie (para placas).

El estudio de la resistencia de materiales sigue un plan que incluye:

• Hipótesis cinemática: Es una suposición sobre cómo se moverán o deformarán las partes de un objeto bajo ciertas fuerzas. Por ejemplo, para una viga, se asume cómo se doblará.
• Ecuación constitutiva: Describe cómo el material responde a las fuerzas. Nos dice cómo se relacionan las deformaciones con las tensiones. Un ejemplo es la ley de elasticidad de Hooke, que dice que muchos materiales se estiran o comprimen de forma proporcional a la fuerza aplicada, hasta cierto límite.
• Ecuaciones de equivalencia: Relacionan las tensiones internas con las fuerzas totales que actúan en una sección del objeto.
• Ecuaciones de equilibrio: Conectan las fuerzas externas que se aplican al objeto con las fuerzas internas que se generan dentro de él.

En la práctica, los ingenieros usan fórmulas ya establecidas para resolver problemas. Los pasos suelen ser:

1. Calcular esfuerzos: Determinar las fuerzas internas que aparecen en el objeto debido a las cargas externas.
2. Analizar la resistencia: Calcular las tensiones (fuerzas por área) en el material para asegurarse de que no superen lo que el material puede soportar.
3. Analizar la rigidez: Calcular cuánto se deforma o desplaza el objeto para verificar que no se mueva más de lo permitido.

¿Qué es una hipótesis cinemática?

Una hipótesis cinemática es una forma de describir matemáticamente cómo se mueven o deforman las partes de un objeto. Esto es muy útil para simplificar los cálculos, especialmente en objetos largos y delgados (como vigas) o planos (como placas).

Gracias a estas hipótesis, en lugar de calcular el movimiento de cada punto en un objeto tridimensional, podemos calcularlo a partir de un conjunto más pequeño de valores, como los movimientos de una línea central o una superficie media.

Hipótesis para objetos largos (elementos lineales)

Para objetos como vigas y pilares, la resistencia de materiales propone que el movimiento de cualquier punto se puede calcular a partir de los movimientos y giros de su eje central. Esto hace que los cálculos sean mucho más sencillos. Algunas hipótesis comunes son:

• La hipótesis de Navier-Bernouilli: Se usa para vigas largas que se doblan, cuando las deformaciones por corte son pequeñas.
• La hipótesis de Timoshenko: Se usa para vigas que se doblan en un caso más general, sin ignorar las deformaciones por corte.
• La hipótesis de Saint-Venant: Se usa para objetos que se estiran o comprimen, especialmente lejos de donde se aplican las cargas.
• La hipótesis de Coulomb: Se usa para objetos que se tuercen, especialmente si tienen una sección circular o tubular.

Hipótesis para objetos planos (elementos superficiales)

Para placas y láminas que se doblan, se usan dos hipótesis principales:

• Hipótesis de Love-Kirchhoff
• Hipótesis de Reissner-Mindlin

¿Qué es una ecuación constitutiva?

Las ecuaciones constitutivas nos dicen cómo se comporta un material. Generalmente, se usan las ecuaciones de Lamé-Hooke de la elasticidad lineal. Estas ecuaciones se pueden adaptar para objetos largos o planos.

Por ejemplo, para objetos largos, las tensiones en cualquier punto de una sección transversal se pueden escribir en función de las deformaciones. Esto significa que si sabemos cuánto se deforma el material, podemos saber qué tensiones internas tiene.

Además de las ecuaciones elásticas, que describen cómo los materiales vuelven a su forma original después de quitar la fuerza, también existen métodos de cálculo plástico. Estos se usan cuando los materiales se deforman permanentemente, es decir, no recuperan su forma original.

¿Qué son las ecuaciones de equivalencia?

Las ecuaciones de equivalencia nos permiten relacionar las tensiones (fuerzas por unidad de área) con los esfuerzos totales que actúan en una sección de un objeto. Esto es útil porque nos permite escribir las ecuaciones de equilibrio de una manera más sencilla, conectando directamente las fuerzas externas con los esfuerzos internos.

Para objetos largos (elementos lineales)

En objetos largos y rectos, como vigas, se usan coordenadas para describir su forma. Las ecuaciones de equivalencia relacionan el esfuerzo normal (fuerza a lo largo del objeto), los esfuerzos cortantes (fuerzas que tienden a cortar el objeto), el momento torsor (fuerza que lo tuerce) y los momentos flectores (fuerzas que lo doblan) con las tensiones internas.

Para objetos planos (elementos bidimensionales)

Para objetos planos como las placas, se usan dos coordenadas para la superficie y una para el espesor. Las ecuaciones de equivalencia relacionan los esfuerzos de membrana (fuerzas que estiran o comprimen la superficie), los momentos flectores (fuerzas que doblan la placa) y los esfuerzos cortantes (fuerzas que tienden a cortar la placa) con las tensiones internas.

¿Qué son las ecuaciones de equilibrio?

Las ecuaciones de equilibrio en la resistencia de materiales conectan los esfuerzos internos de un objeto con las fuerzas externas que se le aplican. Son el resultado de aplicar las leyes de equilibrio de la teoría de la elasticidad a los esfuerzos en lugar de a las tensiones.

Ecuaciones para objetos largos y rectos

Imagina una viga recta y horizontal. Si le aplicamos cargas verticales, las ecuaciones de equilibrio relacionan el momento flector (la fuerza que la dobla) y el esfuerzo cortante (la fuerza que la corta) con la carga vertical aplicada.

Ecuaciones para objetos planos bidimensionales

Para objetos planos como las placas que se doblan, las ecuaciones de equilibrio relacionan los momentos por unidad de ancho (fuerzas que doblan la placa) y los esfuerzos cortantes por unidad de ancho (fuerzas que la cortan) con la carga vertical que se aplica sobre su superficie.

¿Cómo se relacionan esfuerzos y tensiones?

Para diseñar piezas mecánicas, es crucial saber:

• Las tensiones: Para asegurarnos de que no superen lo que el material puede soportar sin romperse.
• Los desplazamientos: Para verificar que el objeto no se deforme más de lo permitido y siga funcionando correctamente.

Aunque la teoría de la elasticidad puede calcular tensiones de forma general, para objetos con formas simples (como vigas o placas), los métodos de la resistencia de materiales son mucho más sencillos y directos.

Para objetos largos o unidimensionales

Las tensiones se pueden calcular combinando fórmulas como la fórmula de Navier para la flexión, la fórmula de Collignon-Jourawski para el corte y las fórmulas para la torsión (cuando el objeto se tuerce).

Los desplazamientos (cuánto se mueve o deforma el objeto) se pueden calcular con métodos como la ecuación de la curva elástica o los teoremas de Castigliano.

Para objetos planos o bidimensionales

La teoría de placas de Love-Kirchhoff es como la versión bidimensional de la teoría de vigas. También se usan métodos especiales para calcular la deflexión (cuánto se dobla) de la superficie media de la placa.

¿Cómo se relacionan esfuerzos y desplazamientos?

Otro aspecto importante en la resistencia de materiales es el estudio de la rigidez. La rigidez es la capacidad de un objeto para resistir la deformación. En muchos diseños, es fundamental asegurarse de que los objetos no se desplacen o deformen más allá de un límite establecido cuando se les aplican fuerzas.

Para calcular las deformaciones a partir de los esfuerzos, se pueden usar varios métodos, como el teorema de Castigliano, las fórmulas de Navier-Bresse, la ecuación de la curva elástica o el método matricial de la rigidez. Para casos más complejos, se recurre a métodos computacionales.

Conceptos relacionados

• Conceptos clave: rigidez, equilibrio mecánico, flexión (doblar), torsión (torcer).
• Mecánica de sólidos deformables: tensión, deformación, elasticidad.
• Plasticidad, Mecánica del daño, Viscoelasticidad.
• Elementos resistentes comunes: vigas, pilares, celosías, arcos.
• Elementos resistentes planos: placas y láminas, membranas.
• Métodos de cálculo: cálculo de esfuerzos, teoremas de Castigliano, ecuaciones de Navier-Bresse, teoremas de Mohr, método matricial de la rigidez, teorema de los tres momentos.
• Stephen Timoshenko, un ingeniero importante en la ingeniería mecánica moderna.

Galería de imágenes

• 

  Un material que se carga en a) compresión, b) tracción, c) cizalladura.

• 

  Ejes usuales para una pieza prismática recta, con una sección transversal recta, a la que se refieren los esfuerzos de sección.

Véase también

En inglés: Strength of materials Facts for Kids