El hotel infinito de Hilbert para niños
El hotel infinito de Hilbert es una idea muy interesante creada por el matemático alemán David Hilbert. Esta idea nos ayuda a entender de forma sencilla algunas cosas sorprendentes sobre el concepto matemático del infinito, especialmente sobre los números muy grandes que van más allá de lo que podemos contar, llamados cardinales transfinitos, que fueron estudiados por el matemático Georg Cantor.
Las ideas de Hilbert usan un hotel con un número infinito de habitaciones para explicar algunas de las paradojas que encontró Georg Cantor. Muchas personas han creado historias divertidas usando esta idea del hotel de Hilbert.
Contenido
¿Qué es el Hotel Infinito de Hilbert?
El Hotel Infinito de Hilbert es un lugar imaginario que tiene un número ilimitado de habitaciones. Esto significa que las habitaciones no se acaban nunca, siempre hay una más. Este concepto nos ayuda a explorar cómo funciona el infinito en las matemáticas de una manera que podemos visualizar.
¿Cómo funciona el infinito más uno?
Imagina que el hotel infinito está completamente lleno, con un huésped en cada una de sus infinitas habitaciones. Parece que no hay espacio para nadie más, ¿verdad? Pero en este hotel especial, siempre hay lugar.
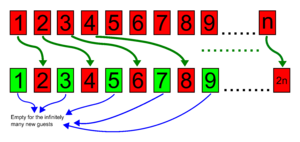
Cuando llega un nuevo huésped, el recepcionista del hotel hace un anuncio: pide a cada huésped que se mueva a la habitación siguiente a la suya. Es decir, el huésped de la habitación 1 se va a la 2, el de la 2 a la 3, y así sucesivamente. Como no hay una "última" habitación, todos tienen un lugar al que ir. De esta manera, la habitación número 1 queda libre para el nuevo huésped. ¡Así, un infinito más uno sigue siendo infinito!
¿Cómo se alojan dos grupos infinitos?
Ahora, piensa que el hotel está lleno y llega un autobús con un número infinito de nuevos turistas. ¡Parece imposible acomodarlos! Pero el recepcionista del Hotel Infinito tiene una solución.
Pide a todos los huéspedes que ya están en el hotel que se muevan a la habitación que resulta de multiplicar el número de su habitación actual por dos. Por ejemplo, el de la habitación 1 se va a la 2, el de la 2 a la 4, el de la 3 a la 6, y así sucesivamente. Esto hace que todos los huéspedes se encuentren en habitaciones con números pares.
De esta forma, todas las habitaciones con números impares quedan libres. Como hay un número infinito de números impares, los infinitos turistas del autobús pueden alojarse sin problema en esas habitaciones. ¡Así, dos infinitos grupos de personas pueden caber en un hotel infinito!
¿Cómo caben infinitos grupos infinitos?
La situación se vuelve aún más compleja: el hotel está lleno y llegan infinitos autobuses, ¡y cada autobús trae un número infinito de turistas! ¿Cómo se puede hacer espacio para tantos? El recepcionista, sin preocuparse, tiene otra solución ingeniosa.
Primero, pide a los huéspedes actuales que se muevan a la habitación que resulta de multiplicar el número de su habitación por dos, igual que antes. Esto libera todas las habitaciones impares.
Luego, el recepcionista asigna un número primo (como 3, 5, 7, 11, etc.) a cada uno de los infinitos autobuses. A cada turista dentro de un autobús se le asigna un número (1, 2, 3, etc.). La habitación de cada turista se calcula elevando el número primo de su autobús a la potencia del número que le tocó al turista. Por ejemplo, si un autobús tiene el número primo 3, el primer turista va a la habitación 3¹ (3), el segundo a la 3² (9), el tercero a la 3³ (27), y así.
Como hay un número infinito de números primos y un número infinito de números para los turistas, se puede encontrar una habitación única para cada uno de los infinitos turistas de los infinitos autobuses. ¡Es una forma asombrosa de ver cómo el infinito puede contener aún más infinito!
Galería de imágenes
Véase también
 En inglés: Hilbert's paradox of the Grand Hotel Facts for Kids
En inglés: Hilbert's paradox of the Grand Hotel Facts for Kids