Operador a nivel de bits para niños
Una operación bit a bit o bitwise es una forma especial de trabajar con números binarios. Los números binarios están hechos de bits, que son como pequeños interruptores que pueden estar en "encendido" (1) o "apagado" (0). Estas operaciones actúan directamente sobre cada uno de esos bits.
Son acciones muy rápidas que los procesadores de las computadoras pueden hacer directamente. En procesadores más sencillos, las operaciones bit a bit son mucho más rápidas que multiplicar o dividir. En los procesadores modernos, son casi igual de rápidas que otras operaciones básicas.
Contenido
Tipos de operaciones con bits
Existen tres tipos principales de operaciones que trabajan con bits:
- Operaciones bit a bit: Realizan operaciones lógicas como AND, OR, XOR y NOT sobre los bits individuales de los números.
- Operaciones de desplazamiento: Mueven los bits de un número hacia la derecha o hacia la izquierda una o más posiciones.
- Operaciones de rotación: Giran los bits de un número hacia la derecha o hacia la izquierda, como si los extremos estuvieran conectados. A veces, usan un bit especial llamado "acarreo" en la rotación.
Operadores bit a bit
Cuando hablamos de la posición de un bit, contamos de derecha a izquierda. El primer bit es el de más a la derecha. Por ejemplo, en el número binario 0001 (que es el 1 en decimal), solo el primer bit está en 1.
NOT: Invirtiendo bits
| A | NOT A |
| 0 | 1 |
| 1 | 0 |
La operación NOT bit a bit, también llamada complemento, es una operación que cambia cada bit de un número. Si un bit es 0, lo convierte en 1. Si es 1, lo convierte en 0. Es como voltear un interruptor.
Por ejemplo: NOT 10011 = 01100
Esta operación es útil para obtener el "complemento a uno" de un número binario. También puede ayudar a cambiar el signo de un número en ciertos sistemas, aunque de una forma un poco especial.
AND: Filtrando y extrayendo bits
| A | B | A AND B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
La operación AND bit a bit toma dos números. Compara cada par de bits en la misma posición. El resultado en esa posición será 1 solo si AMBOS bits son 1. Si alguno de los dos (o ambos) es 0, el resultado es 0.
Por ejemplo: 0101 AND 0011 = 0001
El AND es muy útil para "filtrar" o "enmascarar" bits. Imagina que tienes una plantilla (la máscara) con agujeros. Solo los bits que coinciden con los agujeros (los 1s en la máscara) pasarán.
¿Cómo saber si un bit está encendido?
Puedes usar AND para saber si un bit específico está en 1 (encendido) o en 0 (apagado). Por ejemplo, si tienes el número 0011 y quieres saber si el segundo bit está encendido, usas una máscara 0010 (solo el segundo bit está en 1).
0011 AND 0010 (máscara) = 0010
Como el resultado es diferente de cero, sabes que el segundo bit en el número original (0011) estaba encendido. Esto se llama "enmascaramiento de bits".
Extrayendo partes de un número
AND también sirve para sacar ciertos grupos de bits de un número. Por ejemplo, si tienes un byte (8 bits) que guarda dos números de 4 bits, puedes usar AND con máscaras para separarlos:
0011 0101 AND 1111 0000 (máscara para la primera parte) = 0011 0000 (primera parte extraída)
0011 0101 AND 0000 1111 (máscara para la segunda parte) = 0000 0101 (segunda parte extraída)
Apagando bits específicos
Para apagar bits, usas una máscara con 0s en las posiciones que quieres apagar y 1s en las que quieres dejar igual.
0111 AND 1101 (máscara) = 0101
Aquí, el segundo bit se apagó, mientras que los demás quedaron como estaban.
OR: Encendiendo y combinando bits
| A | B | A OR B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
La operación OR bit a bit también toma dos números. Compara cada par de bits. El resultado en esa posición será 1 si AL MENOS UNO de los bits es 1. Solo será 0 si AMBOS bits son 0.
Por ejemplo: 0101 OR 0011 = 0111
Encendiendo bits específicos
OR es útil para encender bits. Usas una máscara con 1s en las posiciones que quieres encender y 0s en las que quieres dejar igual.
0101 OR 0010 (máscara) = 0111
Aquí, el segundo bit se encendió, y los demás se mantuvieron.
Combinando partes de un número
OR se puede usar para juntar diferentes partes de un número. Imagina que tienes el signo, el exponente y la parte principal de un número flotante (con decimales) en diferentes lugares. Puedes moverlos a sus posiciones correctas y luego usar OR para unirlos en un solo número.
Por ejemplo, para juntar las partes de un número flotante de 32 bits:
Signo: 10000000000000000000000000000000 Exponente: 01000001100000000000000000000000 Parte significativa: 00000000011100000111000000001110 Resultado final: 11000001111100000111000000001110
El resultado final es el número flotante completo.
XOR: Comparando e invirtiendo selectivamente
| A | B | A XOR B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
La operación XOR bit a bit (OR exclusivo) también toma dos números. El resultado en cada posición será 1 si los bits son DIFERENTES (uno es 0 y el otro es 1). Será 0 si los bits son IGUALES (ambos 0 o ambos 1).
Por ejemplo: 0101 XOR 0011 = 0110
Invirtiendo bits de forma selectiva
XOR es genial para invertir solo algunos bits de un número. Si quieres cambiar un bit de 0 a 1 o de 1 a 0, usas una máscara con un 1 en esa posición. Los bits con 0 en la máscara no cambian.
0011 XOR 1010 (máscara) = 1001
Aquí, el primer y tercer bit se invirtieron.
¿Son iguales o diferentes los bits?
XOR también te dice si los bits correspondientes de dos números son iguales o diferentes. Si el resultado de XOR es 0 en una posición, los bits eran iguales. Si es 1, eran diferentes.
1000 XOR 0010 = 1010
El resultado 1010 nos dice que el primer y tercer bit eran diferentes.
Poniendo un registro a cero rápidamente
Los programadores avanzados a veces usan XOR para poner un registro (un espacio de memoria temporal en el procesador) a cero de forma muy eficiente. Si haces XOR de un número consigo mismo (por ejemplo, `A XOR A`), el resultado siempre será cero. Esto es a menudo más rápido que cargar el valor cero directamente.
En resumen
Las operaciones bit a bit (NOT, AND, OR, XOR) te permiten controlar los bits de un número de muchas maneras: encenderlos, apagarlos, dejarlos pasar, eliminarlos o invertirlos. Todo esto se logra usando la máscara adecuada.
0011 1011 10101 10101 1010 OR 1000 (máscara) AND 1110 (máscara) AND 00111 (máscara) AND 11000 (máscara) XOR 1001 (máscara) = 1011 = 1010 = 00101 = 10000 = 0011 Encender el Apagar el Dejar pasar los 3 Eliminar los 3 Invertir los bits bit superior bit inferior bits inferiores bits inferiores inferior y superior
NOT 1011 11010 = 0100 XOR 10100 invertir todos = 01110 (0 = bits iguales, 1 = bits diferentes) los bits AND 00010 (se filtra el segundo bit, que es el que interesa) = 00010 Determinar si los bits de la segunda posición de los dos números son iguales o diferentes 0 = iguales 1 = diferentes
Operaciones de desplazamiento y rotación
Estas operaciones mueven los bits dentro de un número. Aunque no comparan pares de bits como las operaciones AND, OR o XOR, son fundamentales para manipular la representación binaria de los números.
Los registros (pequeños espacios de memoria dentro del procesador) tienen un tamaño fijo. Cuando los bits se mueven, algunos "salen" por un extremo y otros "entran" por el otro. La diferencia entre los tipos de desplazamiento está en cómo se llenan los espacios vacíos.
Desplazamientos de bits
Hay dos tipos principales de desplazamientos: lógicos y aritméticos.
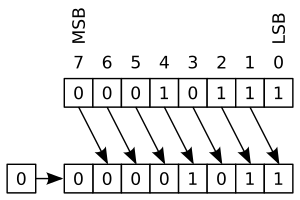
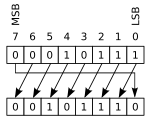
Desplazamiento lógico
En un desplazamiento lógico, los bits se mueven hacia la izquierda o hacia la derecha. Los bits que "salen" por un extremo se pierden. Los espacios vacíos que quedan en el otro extremo se rellenan siempre con ceros.
Por ejemplo, si tienes 10110011 en un registro de 8 bits:
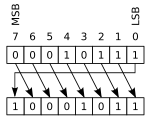
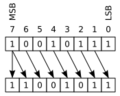
- Desplazamiento a la izquierda (un bit):
1 <-- 0110011 <-- 0 01100110 El 1 de la izquierda se pierde, y un 0 entra por la derecha.
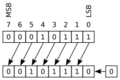
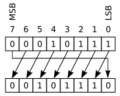
- Desplazamiento a la derecha (un bit):
0 --> 1011001 --> 1 01011001 El 1 de la derecha se pierde, y un 0 entra por la izquierda.
Este tipo de desplazamiento es muy útil para mover bits a la posición correcta, como cuando empaquetas dos números pequeños en un solo byte.
También, para números sin signo, un desplazamiento lógico a la izquierda de 'n' posiciones es como multiplicar por 2 elevado a 'n' (2n). Un desplazamiento lógico a la derecha de 'n' posiciones es como dividir por 2 elevado a 'n' (2n). Por ejemplo, desplazar un bit a la izquierda es multiplicar por 2. Desplazar un bit a la derecha es dividir por 2 (y se pierde cualquier decimal).
Desplazamiento aritmético
Los desplazamientos aritméticos son para números con signo (positivos o negativos). Su objetivo es que la multiplicación o división por potencias de 2 funcione correctamente manteniendo el signo del número.
- El desplazamiento aritmético hacia la izquierda es igual al lógico. Siempre se añade un 0 por la derecha.
- El desplazamiento aritmético hacia la derecha es diferente. Para mantener el signo del número, el bit que entra por la izquierda no es siempre un 0. Si el número original era positivo (su bit de signo era 0), entra un 0. Si el número original era negativo (su bit de signo era 1), entra un 1. Así, el signo del número se mantiene.
Ejemplos con un registro de 8 bits:
- Número positivo (23 en decimal):
00010111 (Decimal 23) Desplazamiento aritmético a la izquierda: 00101110 (Decimal 46) (Se pierde el 0 de la izquierda, entra un 0 por la derecha)
- Número negativo (-41 en decimal):
11010111 (Decimal -41) Desplazamiento aritmético a la izquierda: 10101110 (Decimal -82) (Se pierde el 1 de la izquierda, entra un 0 por la derecha)
- Número positivo (23 en decimal):
00010111 (Decimal 23) Desplazamiento aritmético a la derecha: 00001011 (Decimal 11) (Se pierde el 1 de la derecha, entra un 0 por la izquierda, manteniendo el signo positivo)
- Número negativo (-41 en decimal):
11010111 (Decimal -41) Desplazamiento aritmético a la derecha: 11101011 (Decimal -21) (Se pierde el 1 de la derecha, entra un 1 por la izquierda, manteniendo el signo negativo)
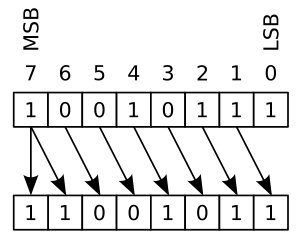
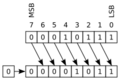
Rotación de bits
Rotación simple
La rotación de bits es como un desplazamiento, pero los bits que salen por un extremo "vuelven a entrar" por el otro. Es como si los bits estuvieran en un círculo. Si un bit sale por la izquierda, entra por la derecha, y viceversa.
Esta operación es útil cuando necesitas mover bits sin perder ninguno. Se usa a menudo en criptografía (para proteger información).
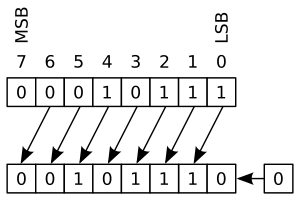
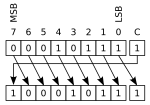
Rotación a través del bit de acarreo
Esta rotación es similar a la anterior, pero incluye un bit especial llamado "bit de acarreo" en el ciclo. El bit que sale del registro va al bit de acarreo, y el bit que estaba en el acarreo entra al registro por el otro extremo.
Esto es muy útil cuando trabajas con números que son más grandes que el tamaño normal de los registros del procesador. Por ejemplo, si un número grande está guardado en dos registros, puedes usar el bit de acarreo para pasar un bit de un registro al otro durante la rotación, como si fuera un solo número muy largo.
Galería de imágenes
Véase también
 En inglés: Bitwise operation Facts for Kids
En inglés: Bitwise operation Facts for Kids