Acústica musical para niños
La acústica musical es una parte de la acústica que estudia cómo funciona la física en la música. Se encarga de investigar cómo se producen los sonidos que usamos para hacer música. También analiza cómo escuchamos la música y busca mejorar los sonidos de los instrumentos musicales, la voz (al hablar y cantar), y ayuda a analizar las melodías con computadoras.
Contenido
- ¿Cómo se estudia la acústica musical?
- ¿Cómo funcionan los sonidos en la música?
- ¿Qué sentimos al escuchar sonidos?
- Armónicos, parciales y sobretonos: ¿cuál es la diferencia?
- Armónicos y sistemas no lineales
- ¿Qué es la armonía musical?
- ¿Qué son las escalas musicales?
- ¿Cómo evolucionaron las escalas musicales?
- Véase también
- Galería de imágenes
¿Cómo se estudia la acústica musical?
Para entender la acústica musical, se usan diferentes métodos:
- Análisis de frecuencia: Se estudia qué tan rápido vibran los sonidos.
- Análisis de la estructura musical: Se examina cómo están organizadas las partes de una pieza musical.
- Creación de sonidos musicales: Se generan nuevos sonidos.
- Reconocimiento musical: Se identifica la música basándose en sus características físicas, lo que también se conoce como psicoacústica.
¿Cómo funcionan los sonidos en la música?
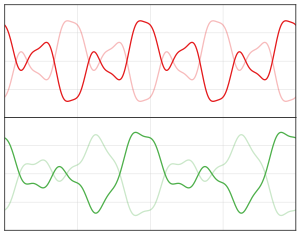
Cuando escuchamos dos sonidos diferentes al mismo tiempo, sus ondas sonoras se mezclan. Las partes altas y bajas de la presión del aire se unen para crear una nueva onda de sonido. Cualquier onda de sonido compleja puede verse como la suma de muchas ondas simples (llamadas ondas sinusoidales) con diferentes velocidades y fuerzas.
Nuestros oídos y cerebro pueden separar estos sonidos y distinguirlos. Cuando varios sonidos se tocan a la vez, la presión del aire en el oído reproduce todas las ondas, y nuestro cerebro las separa para que escuchemos cada sonido por separado.
Cuando los sonidos se repiten de forma perfecta, una nota está formada por varias ondas simples que se relacionan entre sí. La más baja se llama frecuencia fundamental, y las demás son armónicos y sobretonos. La frecuencia fundamental es la velocidad a la que vibra la onda completa. Los sobretonos vibran más rápido, pero lo hacen a múltiplos exactos de la frecuencia fundamental para que la onda final mantenga su ciclo. Los instrumentos reales no son perfectamente periódicos, por lo que los sobretonos pueden ser un poco diferentes, y la forma de la onda cambia ligeramente con el tiempo.
¿Qué sentimos al escuchar sonidos?
Los cambios en la presión del aire que llegan a nuestro oído, y cómo nuestro cuerpo y cerebro los procesan, nos hacen sentir lo que llamamos «sonido». Muchos sonidos que consideramos "musicales" son vibraciones que se repiten regularmente, en lugar de sonidos sin un patrón fijo. A la forma en que el sonido viaja la llamamos «onda sonora».
Por ejemplo, el sonido de una onda simple (sinusoide) hace que la presión del aire suba y baje de forma regular, y lo escuchamos como un tono muy "puro". Puedes producir tonos puros con un diapasón o silbando, aunque los tonos realmente puros (con una sola onda fundamental) solo se logran con aparatos electrónicos o digitales. La velocidad a la que cambia la presión del aire determina la frecuencia del tono, que se mide en ciclos por segundo o hercios. La frecuencia principal que percibimos se llama tono fundamental.
Armónicos, parciales y sobretonos: ¿cuál es la diferencia?
La fundamental es la frecuencia a la que vibra la onda completa de un sonido. Los sobretonos son otras ondas simples que están presentes a frecuencias más altas que la fundamental. Todos los componentes de frecuencia que forman la onda completa, incluyendo la fundamental y los sobretonos, se llaman parciales.
Los sobretonos que son múltiplos exactos de la fundamental se llaman armónicos. Si un sobretono está muy cerca de ser un armónico, a menudo se le llama armónico parcial, o simplemente armónico. A veces, los sobretonos no se parecen a ningún armónico, y entonces se les llama parciales o sobretonos inarmónicos.
La frecuencia fundamental se considera el primer armónico y el primer parcial. La forma de contar los parciales y los armónicos suele ser la misma: el segundo parcial es el segundo armónico, y así sucesivamente. Pero si hay parciales inarmónicos, la numeración no coincidirá. Los sobretonos se numeran según su posición por encima de la fundamental. Técnicamente, el primer sobretono es el segundo parcial (y normalmente el segundo armónico). Como esto puede ser un poco confuso, solo los armónicos se nombran por sus números, y los sobretonos y parciales se describen según su relación con estos armónicos.
Armónicos y sistemas no lineales
Cuando una onda que se repite está formada por una fundamental y solo armónicos impares (como f, 3f, 5f, 7f, etc.), la onda resultante es simétrica. Esto significa que si la volteas y cambias su fase, se verá exactamente igual. Si la onda tiene algún armónico par (como 0f, 2f, 4f, 6f, etc.), será asimétrica, es decir, la parte de arriba no será un reflejo exacto de la de abajo.
Lo contrario también es cierto. Un sistema que cambia la forma de una onda (modificando su tamaño o fase) crea armónicos adicionales. A esto se le llama distorsión armónica y se dice que es un sistema no lineal. Si afecta a la onda de forma simétrica, solo producirá armónicos impares. Si la afecta de forma asimétrica, habrá al menos un armónico par.
¿Qué es la armonía musical?
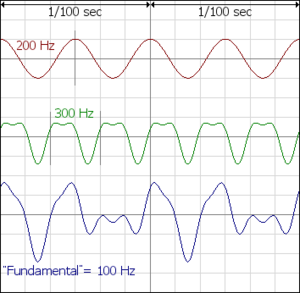
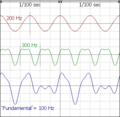
Si se tocan dos notas al mismo tiempo, y sus frecuencias tienen una relación simple (por ejemplo, 2/1, 3/2 o 5/4), la onda combinada seguirá siendo periódica y la mezcla sonará en consonancia (agradable). Por ejemplo, una nota que vibra a 200 Hz y otra a 300 Hz (una quinta perfecta, con una relación de 3/2 sobre 200 Hz) se sumarán para formar una onda que se repite cada 1/100 de segundo. Cada 1/100 de segundo, la onda de 300 Hz se repetirá tres veces y la de 200 Hz dos veces, aunque la onda ya no será simple.
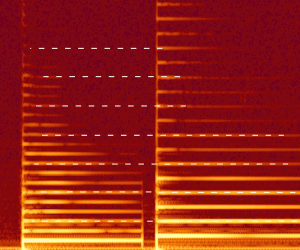
Además, las dos notas tendrán muchos parciales en común. Por ejemplo, la nota de 200 Hz tendrá armónicos en: (200,) 400, 600, 800, 1000, 1200, …
La nota con una frecuencia fundamental de 300 Hz tendrá armónicos en: (300,) 600, 900, 1200, 1500, …
Por lo tanto, las dos notas compartirán los armónicos de 600 y 1200 Hz, y coincidirán más veces en la serie. La combinación de ondas con frecuencias fundamentales pequeñas y parciales o múltiplos cercanos es lo que crea la sensación de armonía.
Cuando dos frecuencias están muy cerca de tener una relación simple, la onda combinada tendrá ciclos tan cercanos que escucharemos una especie de "pulso" constante en lugar de un tono claro. A esto se le llama batimiento o disonancia (sonido que no es agradable).
La frecuencia del batimiento se calcula restando las frecuencias de las dos notas. Siguiendo el ejemplo anterior, [300 Hz - 200 Hz] = 100 Hz. Otro ejemplo: una combinación de dos ondas de 3425 Hz y 3426 Hz produciría un batimiento una vez por segundo (|3425 Hz - 3426 Hz| = 1 Hz). Estos efectos se explican con la teoría de la modulación.
La diferencia entre consonancia y disonancia no es siempre clara, pero el batimiento de frecuencia es clave. Helmholtz sugirió que la mayor disonancia entre dos tonos puros ocurre cuando la velocidad del batimiento es de aproximadamente 35 Hz.
¿Qué son las escalas musicales?
Las notas que se usan en una composición musical suelen elegirse de un grupo llamado escala. Como muchas personas no pueden identificar las frecuencias exactas de las notas, la identidad de una escala se basa en la relación de frecuencias entre sus tonos (conocidos como intervalos).
La escala diatónica ha aparecido en escritos a lo largo de la historia y tiene siete tonos en cada octava. En la entonación natural, la escala diatónica se puede construir fácilmente usando tres intervalos simples dentro de la octava: la quinta justa (3/2), la cuarta justa (4/3) y la tercera mayor (5/4). Estas formas de la quinta y la tercera se encuentran de forma natural en las series armónicas de los resonadores, lo que las hace muy simples.
La siguiente tabla muestra las relaciones entre las frecuencias de todas las notas de la escala y la frecuencia de la primera nota:
| C | D | E | F | G | A | B | C |
|---|---|---|---|---|---|---|---|
| 1 | 9/8 | 5/4 | 4/3 | 3/2 | 5/3 | 15/8 | 2 |
Existen otras escalas que no se basan solo en la entonación natural. Estas escalas tienen sus propios ajustes de intervalos según otros criterios y se conocen como temperamento. El temperamento justo es el más usado. Aunque los temperamentos no tienen la pureza acústica de los intervalos justos, a menudo tienen otras propiedades útiles, como un círculo de quintas cerrado.
¿Cómo evolucionaron las escalas musicales?
Descubrimientos arqueológicos
Muchos expertos creen que las escalas musicales y las tonalidades provienen de los sobretonos naturales.
Se han encontrado pruebas arqueológicas que muestran la existencia de la escala diatónica en pueblos que no conocían las relaciones físicas de los sonidos. Muchos de estos descubrimientos se han hecho en las últimas décadas y sugieren que la evolución de las escalas pudo ser universal o natural. Por ejemplo, se encontró la flauta Neardental de hace 50.000 años. También se descifró la canción más antigua del mundo (de artefactos asirios de hace 4.000 años), que es diatónica y usa armonía basada en terceras, similar a la música antigua inglesa.
Recientemente, se descubrieron varias flautas de 9000 años en China. Una de ellas aún puede tocar 8 notas, incluyendo la octava. Incluso una de las flautas tenía un pequeño agujero extra para mejorar la precisión de la octava nota. (Ver: Jiahu). El hallazgo de Jiahu muestra el desarrollo de otra escala de 7 u 8 notas, que evolucionó de escalas de 5 o 6 notas.
Helmholtz, en su investigación para su libro The Sensations of Tone, también escribió que las escalas se desarrollaron de la misma manera en todas partes, pasando a escalas más largas de 7 notas (y con la octava añadida) hasta llegar a una escala de 8 notas.
Estos descubrimientos, hechos por arqueólogos, muestran similitudes con las escalas actuales.
Una teoría sobre el origen de las escalas
En 1958, el libro Origen de la Música (1970, 1981) propuso que los sobretonos más audibles de los tres intervalos universales (octava, cuarta y quinta) se encuentran dentro del rango de esa octava. Esto da origen a las escalas más comunes: la escala pentatónica, la mayor y la menor (dependiendo de cuántos sobretonos se incluyan).
La diferente intensidad de los sobretonos audibles determina la importancia de cada nota en una escala (como la tónica, la dominante o la subdominante), lo que explica las escalas tonales.
Según la teoría del musicólogo Bob Fink, la escala natural o acústica musical y su tonalidad (una forma de escala con notas fuertes y débiles, no todas de igual importancia) surgieron en la antigüedad de la siguiente manera:
Escuchamos la octava como el sobretono más sonoro de cualquier nota, que sería DO. La siguiente nota más sonora (y diferente) sería un tono que, al bajarlo una octava, coincide con la quinta nota de una escala, llamada la "quinta". En la escala de DO, sería SOL. La nota que produce un DO medio como sobretono audible coincidiría con la cuarta nota de la escala, FA.
Estas creaciones, llamadas tónica, cuarta y quinta, son pasos (o "intervalos") en la escala cuando se tocan fuerte como notas separadas. Este trío de intervalos va del sobretono más notable al más audible de una nota dada.
La tónica, cuarta y quinta se encuentran en las escalas musicales de casi todas las culturas y en todos los periodos de la música humana.
Cuando cada uno de estos intervalos suena como una nota separada, tienen sus propios sobretonos audibles. La influencia de los sobretonos más sonoros de todos estos sonidos sugiere (por un proceso de evolución) que las notas pueden llenar el resto de las notas que se encuentran en las escalas más conocidas en el mundo y en la historia.
Esto también explica por qué hay notas fuertes y débiles en la escala, por qué históricamente solo se aceptaron dos semitonos en la escala y por qué las notas se incorporaron a la escala cuando lo hicieron.
¿Cómo se forman las diferentes escalas?
A continuación, se muestran los sobretonos de estos tres intervalos. Al unir los tres sobretonos (diferentes) más audibles dentro del espacio de una octava, se puede obtener la escala mayor y otras escalas (ignorando los sobretonos de la octava repetida y los sobretonos inaudibles por ser redundantes):
TÓNICA C: Sobretonos: C, G, E, (y Si-bemol; inaudible) QUINTA G: Sobretonos: G, D, B, (y F) CUARTA F: Sobretonos: F, C, A, (y Mi-bemol;)
Usando estas notas y sobretonos, podemos listar estas escalas:
Escala mayor: C, D, E, F, G, A, B, C.
Si reemplazas las tres notas más débiles (la 3.ª, 6.ª y 7.ª de la escala) con otras tres notas (que incluyen el siguiente sobretono par más débil mencionado arriba entre paréntesis), que son bemoles, obtienes la escala menor. (La 6.ª nota de arriba es la más fuerte de las tres porque no forma semitonos con las notas cercanas en la escala mayor. Los semitonos en las escalas, como señaló Helmholtz en Las Sensaciones del Tono, fueron evitados por casi todas las culturas antiguas. «Muchos países evitaron usar intervalos menores de un tono…»):
Escala menor: C, D, Mi-bemol, F, G, La-bemol, Si-bemol, C
Debido a que estos dos sobretonos (correspondientes a las notas Mi y Si) son muy débiles acústicamente, fueron los últimos en incorporarse a la escala. Cómo se reubicaron es un tema de debate histórico. Muchas personas los colocaron en algún punto intermedio entre la menor y la mayor (en las "grietas" del piano), lo que históricamente los hizo conocidos como notas "azules" o "neutras".
O si las notas 3.ª y 7.ª se omitían a la vez (evitando así los semitonos), se obtenían las «notas negras» del piano pentatónico de 5 notas.
Escala pentatónica: C, D, E, G, A, C
Semitonos en la escala y evolución de la armonía
El proceso de añadir semitonos provisionales en la escala pentatónica ocurrió en China, en la música escocesa, etc. Incluso los nombres dados a las notas en diferentes culturas son similares: notas "de paso", "sensibles" y "apropiadas". Parece que fue solo la utilidad de los semitonos lo que finalmente les permitió entrar en las escalas, a medida que estas evolucionaron y fueron reconocidas por varias culturas musicales.
Sin embargo, el Papa Juan XXII en 1322 detuvo este proceso y emitió un decreto contra el uso de la séptima como un tono sensible, prohibiendo su notación en la música escrita. Curt Sachs escribió que los chinos llamaban a los tonos sensibles "pien", que significa "llegando a ser" o "en camino de". Los escoceses hicieron una descripción similar para los tonos principales. Sachs escribió: "La evolución de las escalas en el Este de Asia… comenzó con escalas pentatónicas estrictas". En etapas posteriores, los dos tonos "saltados" (3.ª y 7.ª), como escribió Sachs: «fueron admitidos en las escalas, aunque solo como notas de paso. Finalmente, se incorporaron completamente». (Aparición de la Música en el Mundo Antiguo pp.134-5, véase también Helmholtz' Sensations of Tone, p. 287.)
La armonía evolucionó como una forma de mejorar las relaciones internas de los sobretonos entre las notas en las escalas y las notas en las melodías. Incluso los nombres que surgieron para estas relaciones eran representaciones perfectas de su función acústica o tonal, aunque los nombres ("dominante", "sub-dominante" y "nota clave / tónica") también fueron conocidos por personas sin conocimientos de acústica.
La teoría del trío sugiere que el oído puede distinguir entre sonidos armoniosos y disonantes porque puede percibir estas propiedades acústicas sin tener un conocimiento consciente de ellas o aprenderlas solo por costumbre.
No hay duda de que la acústica por sí sola no puede explicar todas las cuestiones musicales, ya que la psicología, el conocimiento, las costumbres culturales y los gustos también influyen en la evolución de los procesos acústicos descritos aquí.
Véase también
En inglés: Musical acoustics Facts for Kids
Galería de imágenes
-
Onda simétrica y otra asimétrica. La roja contiene el fundamental y los armónicos impares, la verde contiene el fundamental y los pares.
-
Ondas de 200 y 300 y su suma, mostrando los periodos de cada una.
-
Espectrograma de un violín tocando una nota y una quinta justa encima. Los parciales compartidos están resaltados con guiones blancos.
