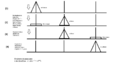
Torres de Hanói para niños
Datos para niños Torres de Hanói |
||
|---|---|---|
| «Torres de Hanói» | ||
 Torres de Hanói
|
||
| Otro nombre | Torres de Brahma o Torres de Lucas | |
| Tipo | Rompecabezas | |
| Inventor | Édouard Lucas | |
| Origen | Francia 1883 |
|
Las Torres de Hanói es un rompecabezas o juego matemático muy conocido. Fue inventado en 1883 por el matemático francés Édouard Lucas.
Este juego individual consiste en varios discos de diferentes tamaños. Estos discos tienen un agujero en el centro y se apilan en uno de los tres postes que están fijos a un tablero. El objetivo es mover toda la pila de discos a otro poste. Para lograrlo, debes seguir algunas reglas importantes. Por ejemplo, nunca puedes poner un disco más grande encima de uno más pequeño. Este problema es muy popular en la ciencia de la computación. Se usa en muchos libros para explicar cómo funcionan los algoritmos.
La fórmula para saber el número mínimo de movimientos necesarios para mover n discos es: 2n - 1.
Contenido
¿Cómo se juega a las Torres de Hanói?
El juego tradicional tiene tres postes verticales. En uno de ellos se apila una torre de discos de madera. Los discos son de diferentes tamaños y están ordenados del más grande al más pequeño, de abajo hacia arriba. Los otros dos postes están vacíos al principio.
El objetivo es mover todos los discos del poste inicial a uno de los postes vacíos. Para hacerlo, debes seguir estas tres reglas sencillas:
- Solo puedes mover un disco a la vez.
- Un disco grande nunca puede ir encima de uno más pequeño.
- Solo puedes mover el disco que esté en la parte superior de cada poste.
Existen varias maneras de resolver este rompecabezas, todas siguiendo diferentes estrategias.
Historia de las Torres de Hanói
El rompecabezas fue creado por el matemático francés Édouard Lucas en 1883. Hay una historia antigua sobre este juego. Se dice que en un templo en la India, en Kashi Vishwanath, hay una sala grande con tres postes muy antiguos. Alrededor de ellos hay 100 discos de oro.
Los sacerdotes de Brahma han estado moviendo estos discos. Lo hacen siguiendo reglas muy antiguas. Por eso, el rompecabezas también se conoce como la Torre de Brahma. La leyenda dice que cuando se haga el último movimiento, el mundo llegará a su fin. No se sabe si Lucas inventó esta leyenda o si se inspiró en ella.
Si la leyenda fuera cierta, y si los sacerdotes movieran un disco por segundo, tardarían muchísimo tiempo. Serían aproximadamente 40.196,9 trillones de años. Esto es mucho más tiempo que la edad actual del Universo.
Hay muchas versiones de esta leyenda. A veces, el templo es un monasterio y los sacerdotes son monjes. También se dice que el templo está en diferentes lugares, como Hanói, Vietnam. En algunas historias, la torre fue creada al principio del mundo. O los sacerdotes solo pueden hacer un movimiento por día.
¿Cómo se resuelve el rompecabezas?
La solución de las Torres de Hanói es fácil de entender. Sin embargo, el número de pasos para resolverlo crece muy rápido a medida que aumentan los discos. Como ya se mencionó, el número mínimo de movimientos es 2n - 1, donde n es la cantidad de discos.
Una forma sencilla de saber si puedes terminar el juego es fijarte en la cantidad de discos. Si es un número impar, el primer disco pequeño irá al poste final. Si es un número par, irá al poste del medio (auxiliar).
Solución sencilla
Una forma de resolver el problema se basa en el disco más pequeño. Este es el que está más arriba en el poste de inicio.
- Si tienes un número par de discos, el primer movimiento del disco más pequeño es hacia el poste del medio.
- Si tienes un número impar de discos, el primer movimiento del disco más pequeño es hacia el poste final.
Después de mover el disco más pequeño, solo hay un movimiento posible para los otros discos. Luego, el disco más pequeño se mueve de nuevo. El truco está en mover el disco más pequeño de forma constante.
Reglas matemáticas de los movimientos
Al resolver el problema, se pueden observar algunas reglas matemáticas interesantes:
- El disco número n (siendo 1 el más pequeño) se mueve por primera vez en el paso 2(n-1). Después de eso, se moverá cada 2n movimientos. Por ejemplo, el disco 1 se mueve en los pasos 1, 3, 5, 7, etc.
- El número de veces que se mueve cada disco es 2(n-k). Aquí, n es el número total de discos y k es 1 para el disco más pequeño.
- El número mínimo de movimientos para resolver el problema es (2n)-1, donde n es el número de discos.
- Todos los discos impares (empezando por el 1, el más pequeño) siguen un patrón de movimiento. Los discos pares siguen el patrón inverso. Por ejemplo, si mueves un número impar de piezas del poste 1 al 3:
* Los discos impares se moverán así: 1 -> 3 -> 2 -> 1 -> 3 -> 2, y así sucesivamente. * Los discos pares se moverán así: 1 -> 2 -> 3 -> 1 -> 2 -> 3, y así sucesivamente.
- Estos patrones cambian si el número total de discos es par o impar.
Variantes del juego
Henry Dudeney propuso una variante en su libro The Canterbury Puzzles (1907). Esta variante se llama «Problema del almojarife» y usa cuatro postes en lugar de tres.
En 1939, J. S. Frame y B. M. Stewart propusieron un método para resolver este problema. Este método implica mover grupos de discos en varias etapas. Primero, se mueven los discos más pequeños a un poste auxiliar. Luego, los discos más grandes se mueven al poste final usando las reglas normales de tres postes. Finalmente, los discos pequeños se mueven del poste auxiliar al poste final.
Aunque este método es muy bueno, encontrar el número mínimo de movimientos en el caso general de cuatro postes sigue siendo un desafío para los matemáticos. Sin embargo, para hasta 30 discos, se ha comprobado que el método de Frame-Stewart es el mejor.
Galería de imágenes
Véase también
 En inglés: Tower of Hanoi Facts for Kids
En inglés: Tower of Hanoi Facts for Kids