Tetración para niños

 , con el tono representando el argumento y el brillo representando el módulo.
, con el tono representando el argumento y el brillo representando el módulo.En matemáticas, la tetración (también conocida como hiper-4) es una operación matemática que sigue a la exponenciación. Se define como una exponenciación repetida. La palabra "tetración" viene de "tetra" (que significa cuatro) y "ción" (que se refiere a la repetición). Esta operación se usa para escribir números muy, muy grandes de una forma más sencilla.
Contenido
¿Qué es la Tetración?
Para entender la tetración, es útil ver cómo se relacionan las operaciones matemáticas básicas. Piensa en ellas como una escalera donde cada paso es una forma de repetir el anterior:
- La suma es la operación más sencilla.
- La multiplicación es como una suma repetida. Por ejemplo, 3 × 4 es como sumar 3 cuatro veces (3 + 3 + 3 + 3).
- La exponenciación es como una multiplicación repetida. Por ejemplo, 3^4 es como multiplicar 3 cuatro veces (3 × 3 × 3 × 3).
- La tetración es el siguiente paso: es como una exponenciación repetida. Por ejemplo, la tetración de 3 con altura 4 (escrito como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {^{4}3} ) es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3^{3^{3^{3}}} .
Todas estas operaciones repetidas forman una jerarquía de "hiperoperaciones". Cada una consiste en repetir la operación del nivel inferior. Aquí te mostramos los primeros cuatro niveles:
- Adición:
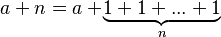
* Esto significa sumar el número 1 a "a" un total de "n" veces.
- Multiplicación:
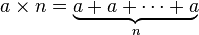
* Esto significa sumar "a" consigo mismo, "n" veces.
- Exponenciación:
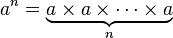
* Esto significa multiplicar "a" por sí mismo, "n" veces.
- Tetración:
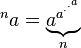
* Esto significa elevar "a" a la potencia de "a", y repetir esto "n" veces.
Cada operación se define usando la repetición de la operación anterior. La siguiente operación en esta serie es la pentación. A diferencia de la suma, multiplicación y exponenciación, que se pueden usar con números complejos, la tetración es más complicada de generalizar para esos casos.
¿Cómo se define la Tetración?
Para cualquier número real positivo Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a > 0 y un número entero no negativo Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): n \ge 0 , la tetración 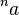 se define así:
se define así:
- Si
 , entonces Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {^{0}a} = 1 .
, entonces Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {^{0}a} = 1 . - Si
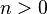 , entonces Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {^{n}a} = a^{\left[^{(n-1)}a\right]} .
, entonces Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {^{n}a} = a^{\left[^{(n-1)}a\right]} .
Ejemplos de Torres de Exponentes
Cuando calculamos una tetración, la vemos como una "torre de exponentes". Es muy importante saber que la exponenciación se resuelve de arriba hacia abajo (o de derecha a izquierda). Si lo haces en otro orden, el resultado será diferente y ¡incorrecto!
Por ejemplo, para calcular Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \,\! ^{4}2 : 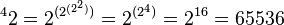
Si lo calculáramos de otra manera (que sería incorrecta): Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \,\!\ ((2^{2})^{2})^{2} = ({4^{2}})^{2} = 16^{2} = 256
Como puedes ver, el orden importa mucho. Las torres de exponentes siempre deben evaluarse de arriba hacia abajo.
Propiedades de la Tetración
La tetración tiene algunas propiedades parecidas a la exponenciación, pero también otras que son únicas. Como la exponenciación no es asociativa (el orden de las operaciones importa), la tetración tampoco sigue algunas reglas simples que vemos en la multiplicación o la suma.
Sin embargo, la tetración tiene una propiedad interesante que se basa en su definición recursiva: 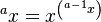 .
.
Esto significa que puedes "descomponer" una tetración en una exponenciación donde el exponente es una tetración de un nivel menor.
Cuando un número x y 10 no tienen factores comunes (son coprimos), podemos calcular las últimas cifras decimales de 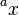 usando el teorema de Euler. Esto también funciona en otros sistemas numéricos, como el octal.
usando el teorema de Euler. Esto también funciona en otros sistemas numéricos, como el octal.
Generalizaciones de la Tetración
La tetración se puede extender de varias maneras, cambiando la base (el número "a") o la altura (el número "n"). Aunque se puede intentar generalizar la base y la altura más allá de los números enteros, las propiedades de la tetración hacen que esto sea más complicado que con otras operaciones.
Bases Especiales
Base Cero
La expresión 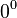 no tiene una definición única en matemáticas. Por eso, las tetraciones con base cero, como
no tiene una definición única en matemáticas. Por eso, las tetraciones con base cero, como 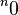 , no están definidas directamente. Sin embargo, si nos acercamos a cero con un número muy pequeño, el resultado de la tetración sí está bien definido:
, no están definidas directamente. Sin embargo, si nos acercamos a cero con un número muy pequeño, el resultado de la tetración sí está bien definido:
- Si n es un número par, el límite es 1.
- Si n es un número impar, el límite es 0.
Así, podemos definir Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {}^{n}0 basándonos en estos límites. Por ejemplo,  , lo que mantiene la regla de que cualquier número elevado a la potencia de 0 es 1.
, lo que mantiene la regla de que cualquier número elevado a la potencia de 0 es 1.
Bases Complejas
Como los números complejos (que tienen una parte real y una parte imaginaria, como a + bi) pueden elevarse a potencias, la tetración también se puede aplicar a ellos. Por ejemplo, para calcular 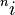 (donde i es la unidad imaginaria), se usan conceptos avanzados de logaritmos y la fórmula de Euler. Esto nos permite encontrar valores aproximados para la tetración de números complejos.
(donde i es la unidad imaginaria), se usan conceptos avanzados de logaritmos y la fórmula de Euler. Esto nos permite encontrar valores aproximados para la tetración de números complejos.
Alturas Especiales
Alturas Infinitas
La tetración puede extenderse a alturas infinitas. Esto significa que para ciertos valores de la base a, la tetración converge a un número finito incluso si la torre de exponentes es infinita. Por ejemplo, la torre infinita 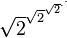 se acerca a 2.
se acerca a 2.
En general, una torre de exponentes infinita 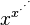 converge a un valor si la base x está en un rango específico, aproximadamente entre 0.066 y 1.44. Este resultado fue demostrado por el famoso matemático Leonhard Euler. Si el límite existe, es una solución de la ecuación Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y = x^y .
converge a un valor si la base x está en un rango específico, aproximadamente entre 0.066 y 1.44. Este resultado fue demostrado por el famoso matemático Leonhard Euler. Si el límite existe, es una solución de la ecuación Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y = x^y .
Alturas Negativas
Podemos usar la regla de la tetración para intentar definirla para alturas negativas. Si usamos la definición recursiva Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {^{k+1}a} = a^{\left({^{k}a}\right)} , podemos reordenarla para encontrar Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {^{k}a} = \log_a \left({^{k+1}a}\right) .
Si sustituimos k por -1, obtenemos: 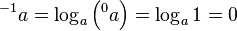 .
.
Esto significa que la tetración con altura -1 es 0. Sin embargo, si intentamos ir más allá, por ejemplo, a una altura de -2, obtenemos Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {}^{-2}a = \log_{a} \left( {}^{-1}a \right) = \log_a 0 , que no está definida en los números reales.
Alturas Reales
Actualmente, no hay una forma única y aceptada de extender la tetración a números reales o complejos para la altura n. Sin embargo, los matemáticos han explorado diferentes maneras de hacerlo. El objetivo es encontrar una "función superexponencial" 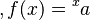 que funcione para números reales x mayores que -2 y que cumpla con las siguientes condiciones:
que funcione para números reales x mayores que -2 y que cumpla con las siguientes condiciones:
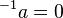

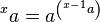 para cualquier número real
para cualquier número real 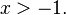
Véase también
 En inglés: Tetration Facts for Kids
En inglés: Tetration Facts for Kids
- Hiperoperación
- Pentación
Enlaces externos




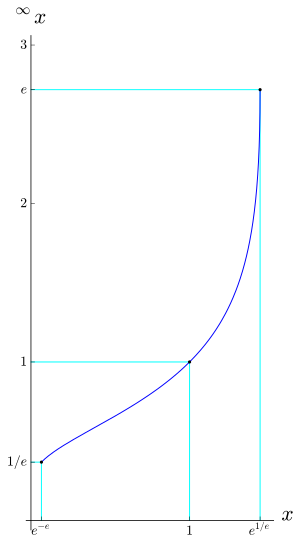
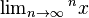 de la exponencial infinitamente iterada converge para las bases
de la exponencial infinitamente iterada converge para las bases 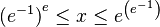 .
.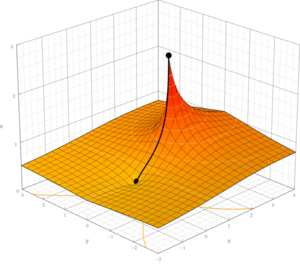
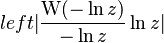 en el plano complejo, mostrando la función exponencial infinitamente iterada de valor real (curva negra)
en el plano complejo, mostrando la función exponencial infinitamente iterada de valor real (curva negra)