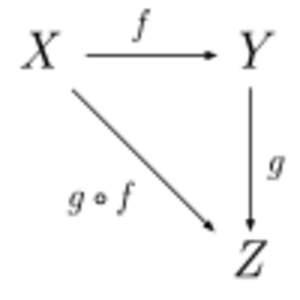Teoría de categorías para niños

Una categoría con objetos X,Y,Z y morfismos f, g, y g∘f.

La teoría de categorías es una rama de las matemáticas que nos ayuda a entender diferentes estructuras matemáticas de una manera nueva y abstracta. Imagina que en lugar de estudiar los "ladrillos" individuales de las matemáticas (como los números o los puntos), nos enfocamos en cómo esos ladrillos se conectan entre sí.

Esta teoría usa dos ideas principales:

• Objetos: Son como los "puntos" o "cosas" que estamos estudiando.
• Morfismos: Son como las "flechas" o "conexiones" que van de un objeto a otro. Estas flechas muestran cómo los objetos se relacionan o se transforman.

La teoría de categorías nos permite ver las matemáticas de una forma más general, sin preocuparnos tanto por los detalles internos de cada cosa, sino por sus relaciones.

Historia de la teoría de categorías

La teoría de categorías fue creada por los matemáticos Samuel Eilenberg y Saunders Mac Lane en 1942. Ellos la desarrollaron mientras trabajaban en un área de las matemáticas llamada topología algebraica. Su objetivo era encontrar una forma más clara de organizar y entender ideas complejas.

Al principio, esta teoría ayudó a resolver problemas en el álgebra abstracta, que es el estudio de estructuras matemáticas como grupos y anillos. Con el tiempo, la teoría de categorías se hizo más general y flexible, ofreciendo una nueva perspectiva para muchas áreas de las matemáticas y la lógica. Incluso algunos científicos la usan para pensar en conceptos de la física.

¿Por qué se llama "categoría"?

El nombre "categoría" viene de una idea del filósofo Kant. En matemáticas, se usa para referirse a una "forma pura" o un tipo de estructura, pero solo dentro del mundo de las matemáticas. Es decir, no tiene un significado fuera de este campo.

Funtores: Puentes entre categorías

Una categoría nos ayuda a entender un grupo de objetos matemáticos y las relaciones entre ellos. Por ejemplo, podemos tener una categoría de "grupos" (un tipo de estructura matemática) donde los objetos son los grupos y los morfismos son las conexiones que mantienen la estructura de esos grupos.

Una vez que tenemos una categoría, podemos relacionarla con otras categorías usando algo llamado funtor. Piensa en un funtor como un "puente" o un "traductor" entre dos categorías. Un funtor toma un objeto de una categoría y lo convierte en un objeto de la otra categoría. También toma las flechas (morfismos) de la primera categoría y las convierte en flechas de la segunda.

Por ejemplo, algunas construcciones matemáticas, como el grupo fundamental de un espacio topológico (que describe los "agujeros" de una forma), pueden expresarse como funtores.

¿Qué es una categoría?

Para que algo sea una categoría, debe cumplir con ciertas reglas:

• Objetos: Debe tener una colección de "cosas" o "puntos" que llamamos objetos.
• Morfismos: Para cada par de objetos, debe haber un conjunto de "flechas" o "conexiones" que van de un objeto a otro. Estas flechas se llaman morfismos. Por ejemplo, una flecha de A a B se escribe como f: A → B.
• Composición de morfismos: Si tienes una flecha de A a B (llamémosla f) y otra flecha de B a C (llamémosla g), puedes combinarlas para obtener una nueva flecha que va directamente de A a C. Esto se llama composición y se escribe g∘f.
• Asociatividad: Si tienes tres flechas que puedes componer (h∘(g∘f)), el orden en que las compones no importa. El resultado es el mismo que ((h∘g)∘f).
• Identidad: Cada objeto tiene una flecha especial que va de él a sí mismo. Esta flecha se llama "morfismo identidad" (I_A). Es como no hacer nada: si combinas cualquier flecha con la identidad, la flecha original no cambia.

Subcategorías: Categorías dentro de otras

Una subcategoría es como una categoría más pequeña que está "dentro" de una categoría más grande. Para que sea una subcategoría, debe cumplir que:

• Sus objetos son parte de los objetos de la categoría grande.
• Sus morfismos (flechas) son parte de los morfismos de la categoría grande.
• La forma en que se componen las flechas y las flechas de identidad son las mismas que en la categoría grande.

Ejemplos de categorías

La teoría de categorías se aplica a muchos tipos de estructuras matemáticas:

• Categoría de Conjuntos (Set): Los objetos son todos los conjuntos (colecciones de cosas) y los morfismos son las funciones entre ellos.
• Categoría de Espacios Topológicos (Top): Los objetos son los espacios topológicos (formas con una idea de "cercanía") y los morfismos son las aplicaciones continuas (funciones que no "rompen" la forma).
• Categoría de Grupos (Grp): Los objetos son los grupos (conjuntos con una operación que cumple ciertas reglas) y los morfismos son los homomorfismos (funciones que conservan la estructura del grupo).
• Categoría de Espacios Vectoriales (Vec): Los objetos son los espacios vectoriales (conjuntos donde puedes sumar vectores y multiplicarlos por números) y los morfismos son las aplicaciones lineales (funciones que conservan las operaciones de los espacios vectoriales).
• Categoría de Anillos (An): Los objetos son los anillos (conjuntos con dos operaciones, como la suma y la multiplicación) y los morfismos son las funciones entre ellos que conservan esas operaciones.
• Categoría de Grafos: Un grafo (como una red de puntos y líneas) puede verse como una categoría. Los objetos son los puntos (vértices) y los morfismos son los caminos que puedes seguir entre los puntos.

Tipos especiales de morfismos (flechas)

Dentro de una categoría, algunas flechas tienen propiedades especiales:

• Monomorfismo: Es una flecha que, si la usas para "cancelar" otras flechas, funciona como una flecha "uno a uno".
• Epimorfismo: Es una flecha que, si la usas para "cancelar" otras flechas, funciona como una flecha "sobre" (que cubre todo el destino).
• Isomorfismo: Es una flecha que tiene una "flecha inversa". Si una flecha es un isomorfismo, significa que los dos objetos que conecta son esencialmente "iguales" o "equivalentes" desde el punto de vista de la categoría.
• Endomorfismo: Es una flecha que va de un objeto a sí mismo.
• Automorfismo: Es un endomorfismo que también es un isomorfismo. Es una transformación de un objeto en sí mismo que es "reversible".

Tipos especiales de objetos

Algunos objetos en una categoría también son especiales:

• Objeto inicial: Es un objeto desde el cual solo hay una única flecha posible hacia cualquier otro objeto en la categoría.
• Objeto final: Es un objeto al cual solo hay una única flecha posible desde cualquier otro objeto en la categoría.
• Objeto nulo: Es un objeto que es inicial y final al mismo tiempo.

Ejemplos de objetos especiales

• En la categoría de Conjuntos (Set), el Conjunto vacío (el conjunto que no tiene elementos) es un objeto inicial.
• Cualquier conjunto que tenga un solo elemento es un objeto final en la categoría de Conjuntos.

Tipos de funtores

Los funtores, que son los "puentes" entre categorías, también pueden ser de diferentes tipos:

• Funtor covariante: Mantiene la dirección de las flechas. Si una flecha va de A a B en la primera categoría, el funtor la transforma en una flecha que va de F(A) a F(B) en la segunda categoría.
• Funtor contravariante: Invierte la dirección de las flechas. Si una flecha va de A a B en la primera categoría, el funtor la transforma en una flecha que va de F(B) a F(A) en la segunda categoría.

Si dos categorías son tan parecidas que un funtor puede "traducir" perfectamente una en la otra y viceversa, decimos que son equivalentes.

Ejemplos de funtores

• Funtor identidad: Es un funtor que no cambia nada. Simplemente toma una categoría y la devuelve exactamente igual.
• Funtor de inclusión: Si tienes una subcategoría, el funtor de inclusión simplemente "incluye" esa subcategoría en la categoría más grande, sin cambiar sus objetos ni flechas.
• Funtores "Olvido": Son funtores que "olvidan" parte de la estructura de un objeto. Por ejemplo, un funtor puede tomar un anillo (que tiene suma y multiplicación) y convertirlo en un grupo (que solo tiene suma), "olvidando" la multiplicación.

Transformaciones naturales

Así como los funtores son "puentes" entre categorías, las transformaciones naturales son como "puentes" entre funtores. Nos permiten comparar dos funtores que van de la misma categoría a la misma categoría. Una transformación natural es una colección de flechas que conectan los resultados de un funtor con los resultados del otro, de una manera "consistente".

Construcciones universales

La teoría de categorías nos ayuda a definir conceptos importantes de una manera muy general, como:

• Producto: Imagina que tienes varias cosas y quieres combinarlas de la manera más general posible. El producto en teoría de categorías es una forma de hacer esto, como cuando combinas dos conjuntos para formar pares ordenados.
• Coproducto: Es lo opuesto al producto. Es una forma de "unir" varias cosas de la manera más general.

Estos conceptos generales son muy útiles porque se aplican a muchos tipos diferentes de estructuras matemáticas.

Otros conceptos importantes

La teoría de categorías tiene muchas otras ideas interesantes:

• Lema de Yoneda: Es un resultado muy famoso que ayuda a entender cómo se relacionan los objetos con las flechas en una categoría.
• Límites y colímites: Son ideas más avanzadas que generalizan los conceptos de producto y coproducto, permitiendo combinar o unir objetos de formas más complejas.
• Funtores adjuntos: Son pares de funtores que están relacionados de una manera especial, como si uno fuera el "opuesto" del otro, pero de una forma más flexible que una simple inversión.
• Diagramas conmutativos: En la teoría de categorías, es muy común usar dibujos con objetos y flechas (diagramas) para mostrar cómo se relacionan las cosas. Un diagrama es "conmutativo" si, no importa qué camino sigas a través de las flechas, el resultado final es el mismo.

Galería de imágenes

• 

  Diagrama de un producto en teoría de categorías.

• 

  Diagrama de un coproducto en teoría de categorías.

Véase también

En inglés: Category theory Facts for Kids