Ábaco neperiano para niños
El ábaco de Napier es una herramienta de cálculo especial que fue inventada por John Napier. Él explicó cómo usarla en un libro llamado Rhabdologia, publicado en Edimburgo a finales de 1617. Con este ábaco, las multiplicaciones se vuelven sumas y las divisiones se convierten en restas. Es parecido a cómo sus tablas de logaritmos, también inventadas por él, ayudan a cambiar operaciones más complejas en otras más sencillas.
Contenido
¿Cómo es el ábaco de Napier?
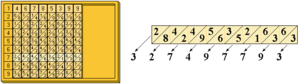
El ábaco de Napier tiene un tablero con un borde. En este tablero se colocan unas varillas especiales, llamadas varillas neperianas, para hacer multiplicaciones o divisiones. El lado izquierdo del tablero tiene 9 espacios donde se escriben los números del 1 al 9.
Las varillas neperianas son tiras hechas de madera, metal o cartón grueso. La parte de adelante de cada varilla está dividida en 9 cuadrados. Todos, menos el de arriba, están divididos por una línea diagonal.
En el primer cuadrado de cada varilla se escribe un número. Los cuadrados de abajo se llenan con el doble, el triple, el cuádruple y así sucesivamente, hasta nueve veces ese número.
Los números que resultan de las multiplicaciones se escriben uno a cada lado de la línea diagonal. Si el número es menor que 10, se escribe en la parte de abajo, y se pone un cero en la parte de arriba.
Un juego completo de estas varillas tiene 9 varillas, una para cada dígito del 1 al 9. Aunque existe una varilla para el 0, no suele ser necesaria para los cálculos.
¿Cómo multiplicar con el ábaco de Napier?
Para multiplicar, por ejemplo, el número 46785399 por 7, se hace lo siguiente:
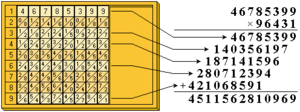
Primero, se colocan en el tablero las varillas que corresponden a cada dígito del número 46785399. La imagen muestra cómo se vería. Después, se lee el resultado en la fila horizontal que está junto al número 7 del tablero. Esta lectura solo necesita sumas sencillas, llevando los números que están en diagonal.
Empezando por la derecha, se obtienen las unidades (3), luego las decenas (6+3=9), las centenas (6+1=7), y así sucesivamente.
Si alguno de los dígitos del número que quieres multiplicar es cero, simplemente se deja un espacio vacío entre las varillas.
Si quisieras multiplicar el número anterior por 96.431, harías lo mismo. Obtendrías rápidamente los resultados de multiplicar el número por 9, 6, 4, 3 y 1 por separado. Luego, los colocarías correctamente y los sumarías para obtener el resultado final.
¿Cómo dividir con el ábaco de Napier?
También se pueden hacer divisiones. Una vez que tienes los 9 resultados de multiplicar el divisor por cada dígito (del 1 al 9) usando el ábaco, solo tienes que elegir el número más cercano y menor al resto. Esto evita tener que adivinar o probar muchos números, como se hace en las divisiones a mano.
Veamos un ejemplo para dividir 46.785.399 entre 96.431:
- El número a dividir (46.785.399) tiene ocho dígitos y el divisor (96.431) tiene cinco. Esto significa que el resultado (el cociente) tendrá 8 - 5 = 3 dígitos. Podría tener hasta 4 dígitos, pero como el primer dígito del número a dividir (4) es menor que el primer dígito del divisor (9), el cociente será de 3 dígitos.
- Esto significa que hay que mover 2 dígitos del número a dividir, dejando el 467.853 como el número inicial para la resta. Usando la tabla de Napier que ya creaste, buscas el número más cercano y menor a 467.853. Este es 385.724, que es el resultado de multiplicar el divisor por 4. Así, el 4 es parte del cociente. La resta da 82.129.
- Al número que queda (82.129), se le añade el siguiente dígito del número original (el 9), formando 821.299. De nuevo, se resta a 821.299 el número más cercano y menor de la tabla de Napier, que es 771.448. Este número se obtuvo multiplicando el divisor por 8. Así, el 8 es la siguiente parte del cociente. La resta da 49.851.
- Al número más cercano, que es 482.155, cuyo número asociado es el cinco. La resta tiene por resultado 16.364.
- Como 16.364 es menor que cualquiera de los números de la tabla de Napier y ya se obtuvieron los tres dígitos del cociente (4, 8 y 5), la operación ha terminado. El 16.364 es el resto.
El resultado de la división es:
| Nombre | Valor |
| Dividendo | 46.785.399 |
| Divisor | 96.431 |
| Cociente | 485 |
| Resto | 16.364 |
¿Cómo calcular la raíz cuadrada con el ábaco de Napier?
Para encontrar la raíz cuadrada de un número, primero se agrupan sus dígitos de dos en dos, empezando desde la coma decimal hacia la izquierda y hacia la derecha. Por ejemplo, el número 458938,34 se agruparía como 45 89 38, 34.
Se toma el primer grupo de la izquierda (que puede ser un solo dígito). Se busca el número entero más grande cuyo cuadrado sea igual o menor que ese grupo. Este será el primer dígito de la respuesta. Luego, se resta el cuadrado de ese número del primer grupo para obtener un resto.
Por ejemplo, si el primer grupo es 07, el número sería 2 (porque 2x2=4, y 3x3=9 es mayor que 7). El resto sería 7-4=3.
Después, se añade el siguiente grupo de dos dígitos al resto, formando un nuevo número. La siguiente cifra de la respuesta debe ser tal que, al usarla en una fórmula especial, el resultado sea menor que el número actual.
Estas operaciones de multiplicación se pueden hacer fácilmente con el ábaco de Napier. Para esto, se necesita una varilla extra que muestre los cuadrados de los números.
Una vez que se conoce el primer dígito, se colocan en el ábaco las varillas que corresponden al doble de ese dígito. Luego, se añade la varilla de los cuadrados para encontrar el número que cumple la ecuación necesaria. Ese número será el que corresponde a la fila del siguiente dígito de la respuesta. Este número se resta del resto actual para encontrar el nuevo resto.
Veamos un ejemplo: queremos encontrar la raíz cuadrada de 46 78 53 99. Tomamos el primer grupo (46) y buscamos el cuadrado más cercano y menor, que es 36 (6x6=36). El siguiente, 49 (7x7=49), es mayor que 46. Así que el primer dígito de la respuesta es 6. El resto es: 46 - 36 = 10.
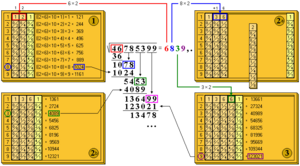
Ahora, colocamos las varillas de 6x2 = 12 en el tablero, y luego la varilla auxiliar de los cuadrados. Juntamos el resto (10) con el siguiente grupo (78), obteniendo 1078. Este número no debe ser superado por el cuadrado de (6b). Al leer en el ábaco, encontramos el valor 1024, lo que nos dice que el siguiente dígito es 8. El nuevo resto es 1078 - 1024 = 54. Bajamos el siguiente grupo (53), obteniendo 5453.
Colocamos las varillas que corresponden al doble de 8. Como 16 es mayor que 10, quitamos la última varilla (la del 2) y la reemplazamos por la del 3 (sumándole una unidad), y añadimos la varilla del 6. El ábaco se ve como en la imagen (2a). Las cifras colocadas corresponden al doble de la solución encontrada hasta ahora (68x2 = 136).
Hecho esto, volvemos a colocar la varilla auxiliar. Operando como antes, obtenemos en la imagen (2b) el tercer dígito: 3. El resto es 1364. Bajamos el siguiente grupo (99), obteniendo 136499. Colocamos la varilla 6 (3x2) y encontramos el siguiente dígito 9. El resto es 13478. Mientras el resto no sea cero, se pueden seguir obteniendo más dígitos.
Por ejemplo, para obtener el primer decimal, bajaríamos el grupo 00, obteniendo 1347800. Luego, colocaríamos las varillas de 9x2 = 18, quedando en el tablero las siguientes: 1-3-6-7(6+1)-8-auxiliar. Al hacer la comprobación, se obtiene que el primer decimal es 9.
Cambios en el diseño del ábaco
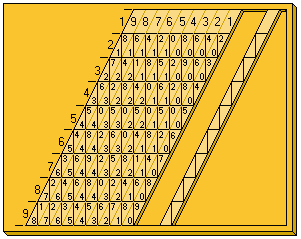
Durante el siglo XIX, el ábaco de Napier fue modificado para que fuera más fácil de leer. Las varillas se empezaron a fabricar con una inclinación de unos 65 grados. Esto hacía que los números que debían sumarse quedaran alineados verticalmente. En este diseño, en cada casilla de la varilla, las unidades se ponían a la derecha y las decenas (o el cero) a la izquierda.
Las varillas estaban hechas de tal manera que las líneas verticales y horizontales eran más visibles que las uniones entre las varillas. Esto facilitaba mucho la lectura, ya que los dos números que formaban cada dígito del resultado quedaban dentro de un rectángulo.
Así, en la imagen se puede ver fácilmente que:
- 987654321 x 5 = 4938271605
Ábaco de fichas
Además del ábaco de varillas, Napier también creó un ábaco con fichas. Juntos, estos dos aparatos forman una pieza histórica muy valiosa y única en Europa. Se encuentra en el Museo Arqueológico Nacional de España.
Este aparato es una hermosa caja de madera con adornos de hueso. En la parte de arriba tiene el ábaco de varillas, y en la parte de abajo está el segundo ábaco. Este segundo ábaco tiene 300 fichas guardadas en 30 cajones. Cien de estas fichas tienen números, y doscientas tienen pequeños agujeros triangulares. Estos agujeros permiten ver solo ciertos números de las fichas numeradas cuando se colocan encima. De esta manera, al combinar las fichas de forma inteligente, se pueden hacer multiplicaciones de números muy grandes, ¡hasta un número de 100 dígitos por otro de 200!
En las puertas de la caja también se encuentran las primeras potencias de los números de un solo dígito, los números que se usan en las primeras potencias de un binomio (una expresión matemática), y datos numéricos de los poliedros regulares (formas geométricas con caras planas).
No se sabe quién hizo esta joya tan rica, ni si fue hecha en España o vino de otro país. Es posible que originalmente perteneciera a la Academia de Matemáticas que creó el rey Felipe II, o que fuera un regalo del Príncipe de Gales. Lo único seguro es que se guardaba en el Palacio Real, de donde pasó a la Biblioteca Nacional y luego al Museo Arqueológico Nacional, donde todavía se conserva.
En 1876, el gobierno español envió este aparato a una exposición de instrumentos científicos en Kensington. Allí llamó mucho la atención, tanto que varias sociedades preguntaron a los representantes españoles sobre su origen y uso. Esto hizo que D. Felipe Picatoste escribiera un libro sobre él, que luego fue enviado a muchos países. Fue sorprendente que este ábaco solo fuera conocido en Inglaterra, el país de origen de su inventor.
Galería de imágenes
Véase también
 En inglés: Napier's bones Facts for Kids
En inglés: Napier's bones Facts for Kids